- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по менеджменту на тему Методы принятия управленческих решений
Содержание
- 2. 1. Типы решаемых задач. Методы
- 3. Виды проблем:
- 4. Виды проблем:
- 5. 2. Формализованные методы принятия решений.
- 6. Формализованные методы, используемые для обоснования
- 7. Формализованные методы - методов исследования операций включают:аналитические, статистические, математического программирования, теоретико-игровые
- 8. Аналитические методы характерны тем, что между условиями
- 9. Статистические методы основаны на сборе, обработке и
- 10. Математическое программирование - ряд методов, предназначенных для
- 11. Теоретико-игровые методы служат для обоснования решений в
- 12. 3. Неформализованные методы принятия решений.
- 13. Неформализованные методы принятия решенийметод мозгового штурма;метод Дельфы; метод сценариев, метод дерева решений.
- 14. Метод мозгового штурмаМетод мозгового штурма (или мозговой
- 15. Этапы мозгового штурмаПостановка проблемы. Формулируется проблема. Происходит
- 16. Метод Дельфы - многошаговая циклическая процедура:
- 17. Метод сценариев Под сценарием понимается гипотетическая
- 18. Метод дерева решений Дерево решений представляет
- 19. Метод дерева решений
- 20. Принцип группового выбораПринцип диктатора. В качестве группового
- 21. Принцип группового выбораС = 1/2 (плюс один
- 22. Скачать презентацию
- 23. Похожие презентации





















Слайд 5
2. Формализованные методы принятия решений.
Формализованные
(математические) методы, основаны на получении количественных результатов вычислений, используются
при разрешении хорошо структурированных и частично слабоструктурированных проблемСлайд 6 Формализованные методы, используемые для обоснования и
выбора оптимальных решений, включают:
экономико-математические модели и методы (ЭММ), формализующие
взаимосвязи процессов и явлений;системный анализ, позволяющий выявить взаимодействия составных частей систем, стратегию их развития;
экспертные оценки и суждения, позволяющие квалифицированным специалистам оценить значимость событий, явлений, факторов, прогнозы развития систем и подсистем, соотношение детерминированных и вероятностных факторов.
Слайд 7
Формализованные методы - методов исследования операций
включают:
аналитические,
статистические,
математического
программирования,
теоретико-игровые
Слайд 8 Аналитические методы характерны тем, что между условиями решаемой
задачи и ее результатами устанавливаются аналитические, формульные зависимости
теория вероятностей,
теория марковских процессов,
теория массового обслуживания,
метод динамики средних
Слайд 9 Статистические методы основаны на сборе, обработке и анализе
статистических данных, полученных как в результате статистических действий, так
и выработанных искусственно, путем статистического моделированияпоследовательный анализ дает возможность принимать решения на основе ряда гипотез, каждая из которых сразу же последовательно проверяется;
метод статистических испытаний (метод Монте-Карло) заключается в том, что ход операций проигрывается (моделируется) на ЭВМ со всеми присущими операции случайностями
Слайд 10 Математическое программирование - ряд методов, предназначенных для наилучшего
распределения имеющихся ограниченных ресурсов, а также для составления рационального
плана операцииЛинейное программирование применяется в тех случаях, когда условия выполнения операции описываются системой линейных уравнений или неравенств.
Нелинейное программированияе применяется когда указанные зависимости носят нелинейный характер.
Динамическое программирование служит для выбора наилучшего плана выполнения многоэтапных действий, когда результат каждого последующего этапа зависит от предыдущего.
Слайд 11 Теоретико-игровые методы служат для обоснования решений в условиях
неопределенности обстановки
Теория игр используется в тех случаях, когда неопределенность
обстановки вызвана сознательными, злонамеренными действиями конфликтующей стороны. Теория статистических решений применяется тогда, когда неопределенность обстановки вызвана объективными обстоятельствами, которые либо неизвестны, либо носят случайный характер.
Слайд 12
3. Неформализованные методы принятия решений.
Неформализованные методы
используются при разрешении сложных слабоструктурированных и неструктурированных проблем для
генерирования вариантов решений, их анализа и оценки, выбора и обоснования наилучшего решения.Используются в основном при групповом принятии решений.
Слайд 13
Неформализованные методы принятия решений
метод мозгового штурма;
метод Дельфы;
метод
сценариев,
метод дерева решений.
Слайд 14
Метод мозгового штурма
Метод мозгового штурма (или мозговой атаки)
призван активизировать разработку новых идей и решений в трудных
тупиковых ситуацияхЦель - получение как можно большего количества предложений.
Слайд 15
Этапы мозгового штурма
Постановка проблемы. Формулируется проблема. Происходит отбор
участников штурма.
Генерация идей. Основной этап.
Группировка, отбор и оценка идей.
На этом этапе происходит оценка и выбор окончательной идеи.
Слайд 17
Метод сценариев
Под сценарием понимается гипотетическая картина
последовательного развития во времени и пространстве событий, представляющих в
совокупности эволюцию управляемого объекта в интересующем исследователя разрезе.
Слайд 18
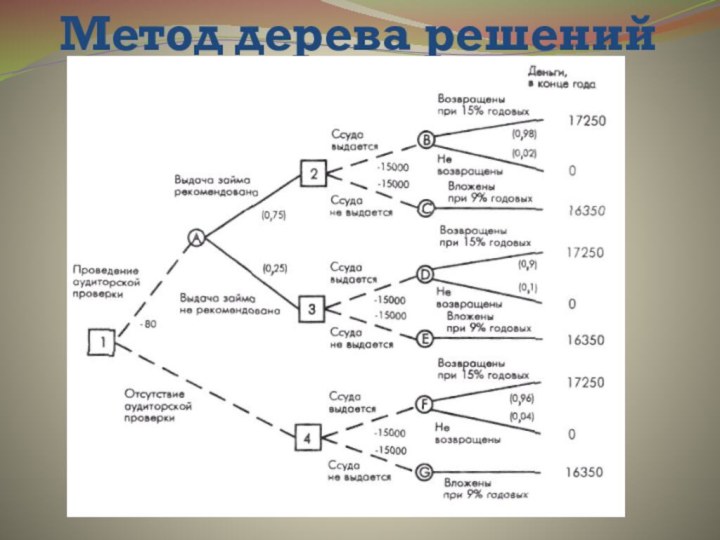
Метод дерева решений
Дерево решений представляет собой
схематичное изображение процесса принятия последовательных решений и состоит из
ветвей — вариантов решений и узлов — соответствующих им исходов.
Слайд 20
Принцип группового выбора
Принцип диктатора. В качестве группового предпочтения
принимается предпочтение одного лица группы.
Принцип большинства голосов. Предпочтительным признается
решение, за которое высказалось число членов группы (голосов), превышающее некоторый порог (С).
Слайд 21
Принцип группового выбора
С = 1/2 (плюс один голос)
— принцип простого большинства голосов;
С = 2/3 —
о принцип большинства в 2/3 голосов (или квалифицированного большинства); С = 1 — соответствует абсолютному большинству голосов.