Знакомство с числами Фибоначчи, с их происхождением,
значением, использованием.
Познакомиться с Числами Фибоначчи
Создать наглядную презентацию о них
Научиться использовать их свойства в математике
Рассказать о них окружающим
Числа Фибоначчи могут быть полезны для математиков, трейдеров, финансистов, экономистов,начинающие инвесторы.
Задачи:
Актуальность:
Слайд 3
Числа фибоначчи- это
Числа Фибоначчи - это целые натуральные числа,
расположенные в числовой последовательности таким образом, что каждое последующее
число является суммой двух предыдущих чисел, при этом в этом числовом ряде проявляются уникальные свойства, выраженные в постоянных отношениях между отдельными членами последовательности, а отношение смежных чисел ряда приближается к отношению, Золотого Сечения, где отношение каждого из этих чисел к последующему члену ряда стремится к величине 0,618 и отношение каждого члена ряда к предыдущему члену стремится к 1,618.
Слайд 4
Волновая теория Эллиотта
и
числа Фибоначчи
Ральф Нельсон Эллиотт
в начале 1930-х г.г. занялся анализом биржевых цен. После
ряда весьма успешных предсказаний он опубликовал в 1939 году серию статей. В них впервые была представлена его точка зрения, что движения индекса Доу-Джонса подчиняются определенным ритмам. Когда соотношение 1.618 (62%) имеет приоритет перед подсчетами волн, можно ввести исчерпывающие правила трейдинга. Приоритет должен быть также и в важности ценовых целей. Большие коррекции с более длительным периодом предпочтительнее краткосрочных форм.
Слайд 5
Уровни Фибоначчи
в волновом техническом анализе
Основные постулаты, на
которых базируется волновая теория Эллиотта, гласят, что структура рынка
обладает волнообразным характером, что дает возможность спрогнозировать развитие ситуации. Волна на фондовом рынке – это движение цен в одном направлении. Ральф Эллиотт разделил рынок на две модели – «бычий» и «медвежий».
Слайд 6
Числа фибоначчи
и технический анализ рынков
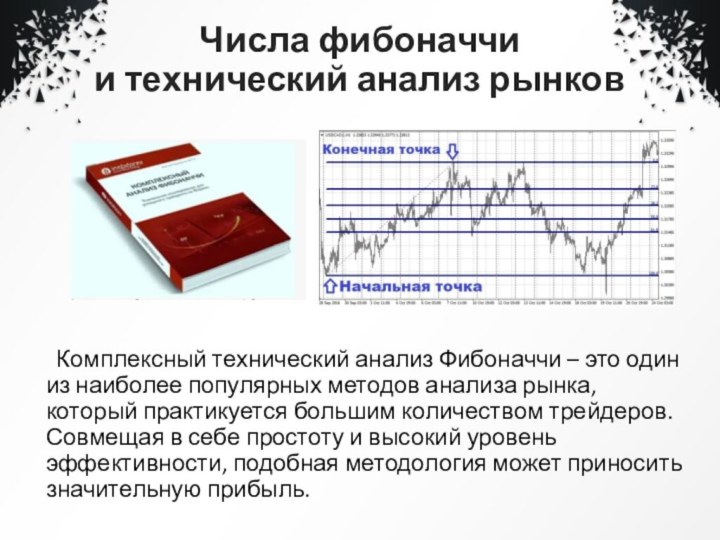
Комплексный технический анализ
Фибоначчи – это один из наиболее популярных методов анализа
рынка, который практикуется большим количеством трейдеров. Совмещая в себе простоту и высокий уровень эффективности, подобная методология может приносить значительную прибыль.
Слайд 7
История жизни
Леонардо Фибоначчи
Леонардо Пизанский (известный как Фибоначчи)
был величайшим математиком Европы . Его отец был купцом.
Путешествуя по Востоку, он познакомился с достижениями арабской математики, способствовал передаче их на Запад. В одном из своих трудов под названием «Книга вычислений» он представил Европе одно из величайших открытий всех времён и народов – десятичную систему счисления. Отец Фибоначчи по торговым делам часто бывал в Алжире и других странах Востока, и Леонардо сопровождал его в торговых экспедициях.
Слайд 8
Работы Фибоначчи
«Книга абака» (Liber abaci), 1202 год, дополнена
в 1228 году;
«Практика геометрии» (Practica geometriae), 1220 год;
«Цветок» (Flos) 1225
год;
«Книга квадратов» (Liber quadratorum), 1225 год;
Di minor guisa, утеряно;
Комментарии к книге X «Начал» Евклида, утеряно;
Письмо Теодорусу, 1225 год.
Слайд 9
Задача Фибоначчи
о размножении кроликов
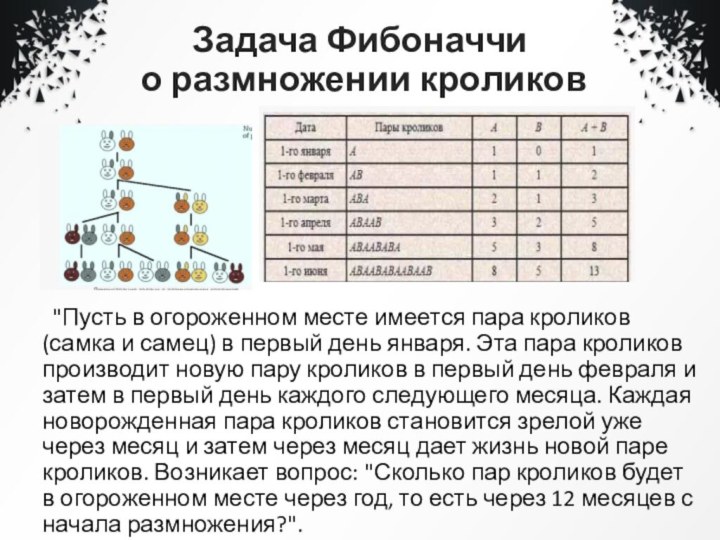
"Пусть в огороженном месте
имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов
производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: "Сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?".
Слайд 10
Математическая сущность числа Фибоначчи
Отношение каждого числа к последующему
более и более стремится к 0,618 при увеличении порядкового
номера. же каждого числа к предыдущему стремится к 1.618 Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (средневековый математик) назвал его Божественной пропорцией. В алгебре общепринято его обозначение греческой буквой фи Ф=1,618.
Слайд 11
Числа Фибоначчи
и золотая пропорция
в теле
человека
Система идеальных пропорций человеческого тела - была разработана древнегреческим
скульптором Поликлетом и в V веке до нашей эры. Ваятель задался целью точно определить пропорции человеческого тела, согласно с его представлениями об идеале. Вот результаты его вычислений: голова - 1/7 всего роста, лицо и кисть руки - 1/10, ступня -1/6.
Слайд 12
Числа Фибоначчи
в живой природе
Первый и очень яркий
пример – это подсолнухи. Их семена расположены так, чтобы
максимально использовать всю площадь соцветия, не теряя ни миллиметра. А расположены они в виде двух пересекающихся спиралей справа налево и наоборот. Пары этих спиралей встречаются разные, у меньших соцветий 13 и 21, 21 и 34, у больших 34 и 55, 55 и 89. И отклонений от этих пар быть не может.
Слайд 13
Нечто подобное происходит и с ячейками ананаса: у
него 8 правосторонних спиралей, 13 левосторонних и 21 вертикальная.
И снова последовательность Фибоначчи. В сосновой шишке, если хорошо присмотреться, можно увидеть две спирали, которые закручены - одна по часовой стрелке, а другая против. Число этих спиралей 8 и 13. Листья на деревьях и других растениях распределены в последовательности, основанной на золотом числе, таким способом, чтобы получать максимум света и не мешать друг другу.