Слайд 2
Содержание
1.1. Временные ряды, их характеристики и задачи анализа
1.2.
Требования к исходной информации
1.3. Аномальные наблюдения, методы их выявления
и анализа
1.4. Методы выявление закономерностей динамики исследуемых явлений
Слайд 3
1.1. Временные ряды, их характеристики и задачи анализа
Динамическим
рядом называется совокупность наблюдений какого-либо явления (показателя), упорядоченная в
зависимости от возрастающих или убывающих значений другого явления (показателя, признака).
Временной ряд – это набор чисел, привязанных к последовательным, обычно равноотстоящим моментам времени. Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.
Числа, составляющие временной ряд и полученные в результате наблюдения за ходом какого-либо процесса, называются уровнями (или элементами) ряда.
Длиной временного ряда называют количество входящих в него уровней.
Слайд 4
1.1. Временные ряды, их характеристики и задачи анализа
Слайд 5
1.1. Временные ряды, их характеристики и задачи анализа
Анализ
временных рядов дает возможность последить развитие явления, показать его
основные пути, тенденции и темпы.
Основные цели анализа временного ряда
описание характерных особенностей ряда;
выяснение механизма, порождающего временной ряд;
подбор статистической модели, описывающей временной ряд;
прогноз будущих значений ряда на основе прошлых наблюдений;
управление процессом, порождающим временной ряд.
Слайд 6
1.1. Временные ряды, их характеристики и задачи анализа
Практическая
реализация перечисленных целей выполняется в результате следующих этапов:
графическое представление
временного ряда;
выделение и удаление: тренда, сезонных и циклических составляющих (выравнивание, сглаживание);
выделение и удаление низко- или высокочастотных составляющих процесса (фильтрация);
исследование случайной составляющей временного ряда, оставшейся после сглаживания и фильтрации;
построение математической модели для описания случайной составляющей и проверка ее адекватности;
прогнозирование будущего развития процесса, описанного временным рядом;
исследование взаимосвязей между различными временными рядами.
Слайд 7
1.1. Временные ряды, их характеристики и задачи анализа
Для
решения перечисленных выше задач используются следующие методы и модели.
методы
корреляционного анализа, позволяющие выявить периодические зависимости и их лаги внутри одного процесса (автокорреляция) или между несколькими процессами (кросскорреляция);
методы спектрального анализа, нацеленные на выявление периодических и квазипериодических составляющих временного ряда;
методы преобразования временных рядов (сглаживание и фильтрация) с целью удаления из них высокочастотных или сезонных составляющих;
модели авторегрессии и скользящего среднего (для описания и прогнозирования случайной составляющей временного ряда).
Слайд 8
1.1. Временные ряды, их характеристики и задачи анализа
Слайд 9
1.1. Временные ряды, их характеристики и задачи анализа
Интервальные
временные ряды представляются последовательностью значений показателей за определенный интервал
времени (год, квартал, месяц и т.д.).
Моментные ряды представляются в виде последовательности показателей, относящихся к конкретным моментам времени (на 1 января, на 1 июля и т. д.).
Особенности уровней интервальных и моментных рядов
1. отдельные уровни моментного временного ряда абсолютных величин содержат элементы повторного счета, то есть в каждом последующем уровне содержится полностью или частично значение предыдущего уровня. Все это делает бессмысленным суммирование моментных рядов.
2. Значения же уровней абсолютных интервальных временных рядов, в отличие от уровней моментного ряда, не содержатся в предыдущих и последующих показателях, их можно просуммировать, что позволяет получать ряды более укрупненных периодов, или ряды с нарастающими итогами
Слайд 10
1.1. Временные ряды, их характеристики и задачи анализа
Временные ряды подразделяются на стационарные и нестационарные.
Случайные процессы,
протекающие во времени приблизительно однородно и имеющие вид непрерывных случайных колебаний вокруг некоторого среднего значения, причем ни средняя амплитуда, ни характеристика этих колебаний не обнаруживают существенных изменений с течением времени в математической статистике называются стационарными.
Всякий стационарный процесс можно рассматривать как процесс, неопределенно долго продолжающийся во времени.
Слайд 11
1.1. Временные ряды, их характеристики и задачи анализа
Стационарным
(строго стационарным или стационарным в узком смысле слова) называется
такой ряд динамики, у которого совместное распределение вероятностей для n уровней y(t1), y(t2), … . y(tn), такое же, что и для n уровней y(t1+τ), y(t2+τ), … , y(tn+τ) для любого t1,t2, …, tn и τ.
Стационарным в широком смысле называется процесс, если постоянны первый и второй моменты, а функция ковариации зависит только от лагового сдвига m и не зависит от времени:
Слайд 12
1.1. Временные ряды, их характеристики и задачи анализа
Стационарность
означает, что среднее значение уровней и их дисперсия –
постоянные величины.
Можно сказать и так: ряд динамики стационарный, если значения его уровней не зависят от начала отсчета.
В экономической практике в большинстве случаев приходится иметь дело со случайными процессами, имеющими вполне определенную тенденцию развития во времени. Такие процессы называются нестационарными, и временные ряды также называются нестационарными.
Характеристики нестационарного случайного процесса меняются во времени, то есть зависят от начала отсчета.
нестационарный ряд: x(k) є ( µ, σ2 ) , µ = var, σ2 = const
где k – это номер наблюдения
Слайд 13
1.1. Временные ряды, их характеристики и задачи анализа
Выбор
вида временного ряда определяется целями анализа.
Временные ряды могут быть
изображены графически. Графическое изображение позволяет наглядно представить развитие явлений во времени и способствует проведению анализа уровней.
Наиболее распространенным видом графического изображения для аналитических целей является линейная диаграмма, которая строится в прямоугольной системе координат.
Наряду с линейной диаграммой для графического изображения временных рядов в целях популяризации широко используются столбиковые, секторные и другие виды диаграмм.
Слайд 14
1.2. Преобразования исходной информации
При обнаружении несопоставимости уровней ряда
может применяться процедура смыкания рядов.
Смыкание может быть произведено
двумя способами:
1. с помощью коэффициента перевода;
2. с помощью формирования относительных величин
Первый способ заключается в том, что данные за предыдущие периоды умножаются на коэффициент перевода, равный отношению показателей на этот момент времени, когда произошло изменение условий формирования уровней ряда. Например, в современных условиях переоценка основных производственных фондов происходит ежегодно, и, следовательно, во временном ряду каждый год становится переходным, что постоянно требует расчета коэффициента перевода.
Слайд 15
1.2. Преобразования исходной информации
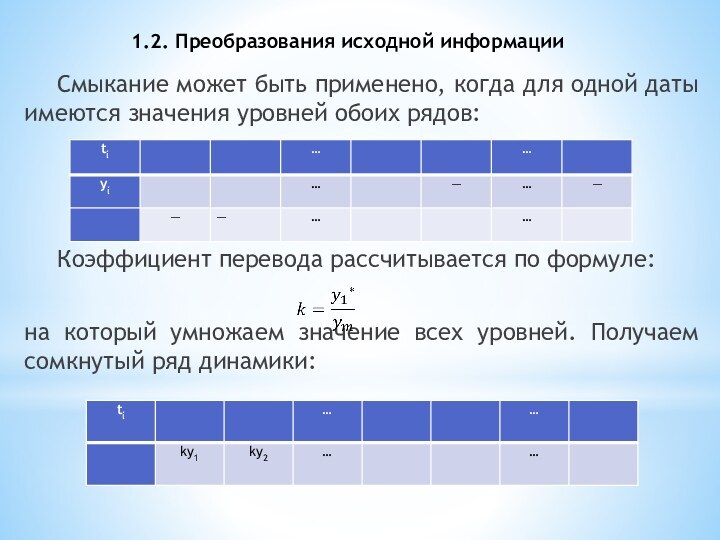
Смыкание может быть применено, когда
для одной даты имеются значения уровней обоих рядов:
Коэффициент перевода
рассчитывается по формуле:
на который умножаем значение всех уровней. Получаем сомкнутый ряд динамики:
Слайд 16
1.2. Преобразования исходной информации
Слайд 17
1.2. Преобразования исходной информации
Способы получения пропущенных значений временного
ряда
Интерполяция, интерполирование — в вычислительной математике это способ нахождения
промежуточных значений величины по имеющемуся дискретному набору известных значений.
Рассмотрим систему несовпадающих точек
( ) из некоторой области D. Пусть значения функции известны только в этих точках:
Задача интерполяции состоит в поиске такой функции F из заданного класса функций, что
Слайд 18
1.2. Преобразования исходной информации
Способы получения пропущенных значений временного
ряда
Точки называют узлами интерполяции, а их
совокупность — интерполяционной сеткой.
Пары называют точками данных или базовыми точками.
Разность между «соседними» значениями
- шагом интерполяционной сетки. Он может быть как переменным, так и постоянным.
Функцию — интерполирующей функцией или интерполянтом.
Слайд 19
1.2. Преобразования исходной информации
Слайд 20
1.2. Преобразования исходной информации
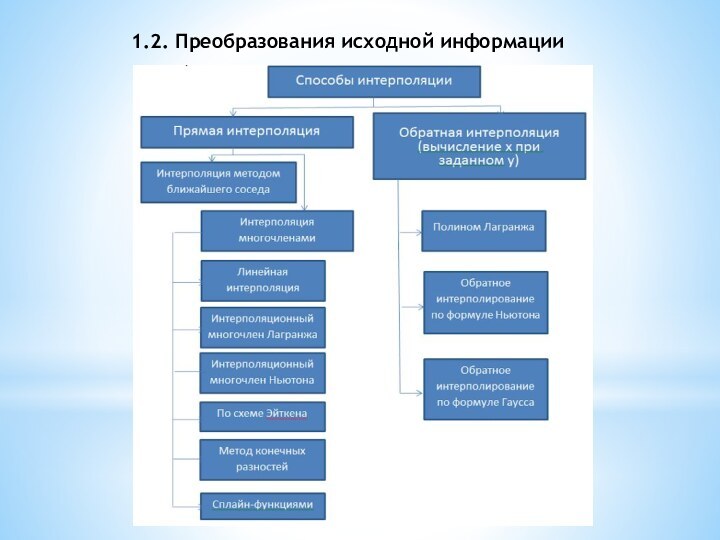
Способы интерполяции
1) Интерполяция методом ближайшего
соседа – простейший способ нахождения недостающего значения уровня ряда
Интерполяция
методом ближайшего соседа (ступенчатая интерполяция) — метод интерполяции, при котором в качестве промежуточного значения выбирается ближайшее известное значение функции. Интерполяция методом ближайшего соседа является самым простым методом интерполяции.
2) Интерполяция многочленами
На практике чаще всего применяют интерполяцию многочленами. Это связано прежде всего с тем, что многочлены легко вычислять, легко аналитически находить их производные и множество многочленов плотно в пространстве непрерывных функций (теорема Вейерштрасса).
Слайд 21
1.2. Преобразования исходной информации
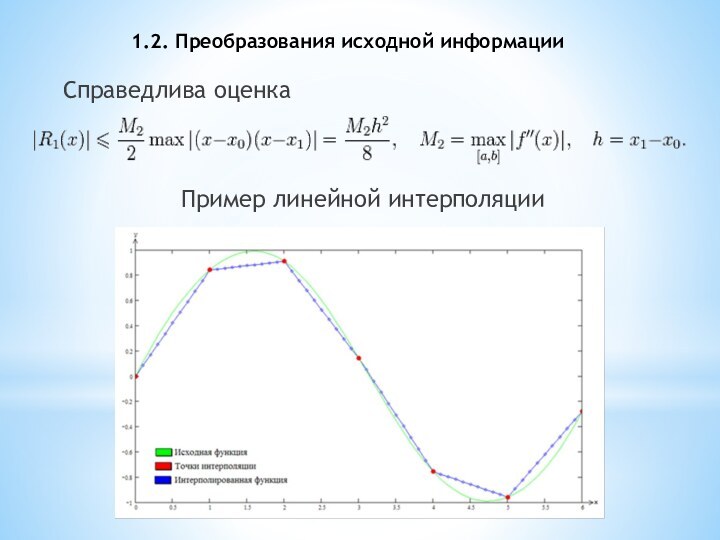
2.1.Линейная интерполяция — интерполяция алгебраическим
двучленом вида P1(x) = ax + b функции f,
заданной в двух точках x0 и x1 отрезка [a, b].
В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией.
Геометрически это означает замену графика функции f прямой, проходящей через точки (x0,f(x0)) и (x1,f(x1)).
Уравнение такой прямой имеет вид:
отсюда для
Это и есть формула линейной интерполяции, при этом
где R1(x) — погрешность формулы:
Слайд 22
1.2. Преобразования исходной информации
Справедлива оценка
Пример линейной интерполяции
Слайд 23
1.2. Преобразования исходной информации
2.2. Полином Лагранжа (интерполяционный
многочлен) - многочлен минимальной степени, принимающий данные значения в
данном наборе точек. Для n + 1 пар чисел
где все xj различны, существует единственный многочлен L(x) степени не более n, для которого L(xj) = yj.
В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.
Лагранж предложил способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
Слайд 24
1.2. Преобразования исходной информации
li(x) обладают следующими свойствами:
1) являются
многочленами степени n;
2) li(xi) = 1;
3) li(xj)
= 0 при
Отсюда следует, что L(x), как линейная комбинация li(x), может иметь степень не больше n, и L(xi) = yi,
Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.
Слайд 25
1.2. Преобразования исходной информации
Этот пример показывает интерполяционный многочлен
Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9),
а также полиномы yi li(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xj
Слайд 26
1.2. Преобразования исходной информации
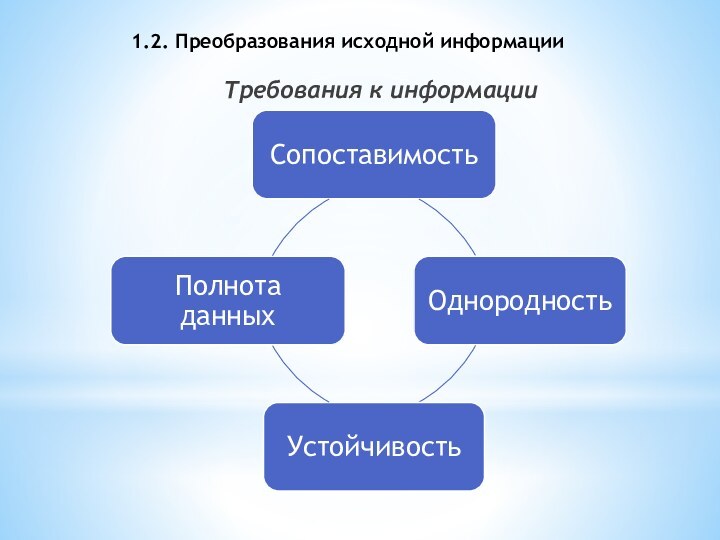
Требования к информации
Слайд 27
1.2. Преобразования исходной информации
Сопоставимость достигается в результате одинакового
подхода к наблюдениям на разных этапах формирования динамического ряда.
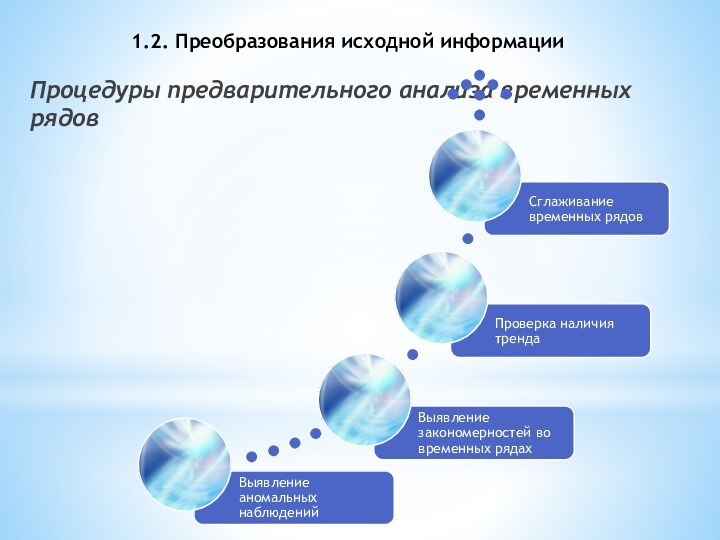
Однородность данных означает отсутствие сильных изломов тенденций, а также аномальных (т.е. резко выделяющихся, нетипичных для данного ряда) наблюдений. Аномальные наблюдения проявляются в виде сильного изменения уровня – скачка или спада – с последующим приблизительным восстановлением предыдущего уровня.
Устойчивость характеризуется преобладанием закономерности над случайностью в изменении уровней ряда.
Требование полноты данных обусловливается тем, что закономерность может обнаружиться лишь при наличии минимально допустимого объема наблюдений.