Слайд 2
Содержание:
Введение
Математические модели и их свойства.
Экономические задачи,
приводящие к исследованию линейной функции.
Использование свойств квадратичной функции
при решении экстремальных задач.
Заключение.
Слайд 3
ВВЕДЕНИЕ:
Большую часть своих усилий человек тратит на поиск
наилучшего, т.е. оптимального решения поставленной задачи. Как, располагая определенными
ресурсами, добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества.
Итак, мы будем различать два вида задач на оптимизацию:
В задачах первого вида улучшение достигается за счет коренных качественных изменений: выбор новых конструктивных решений.
В задачах второго рода качественная сторона дела остается неизменной, но меняются количественные показатели. В данной работе рассмотрены задачи только второго типа. В таких задачах ищутся наибольшее и наименьшее значения функций, зависящих от одной или нескольких переменных.
Слайд 4
Математические модели
и их свойства
Прежде чем решать какую
– либо жизненную задачу, человек старается взвесить имеющуюся у
него информацию, выбрать из нее существенную. И только потом, когда станет более или менее ясно, из чего исходить и на какой результат рассчитывать, он приступает к решению задачи.
В таких случаях необходимо сделать упрощающее предположение, чтобы выделить исходные данные, определить, что будет служить результатом и какова связь между исходными данными и результатом. Все это – предположения, исходные данные, результаты, связи между ними – и называют моделью задачи.
Слайд 5
Экономические задачи, приводящие к исследованию линейной функции
Задача 1:
Расстояние между двумя фермами А и В по
шоссейной дороге 60 км. На ферме А надаивают 200 т молока в сутки, на ферме В – 100 т молока в сутки. Где нужно построить завод по переработке молока, чтобы для его перевозки количество тонно-километров было наименьшим?
Слайд 6
Решение:
Предположим, что завод построили на середине АВ:
200 т
∙ 30 км + 100 т ∙ 30 км
= 9000 т/км
Слайд 7
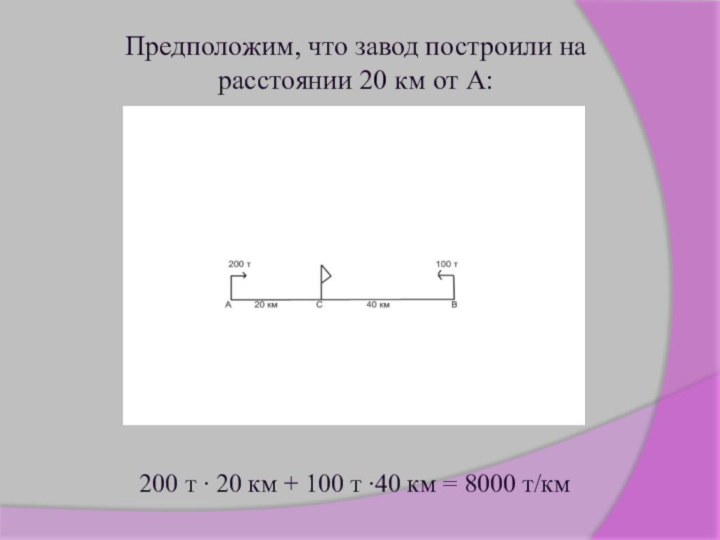
Предположим, что завод построили на расстоянии 20 км
от А:
200 т ∙ 20 км + 100 т
∙40 км = 8000 т/км
Слайд 8
Предположим, что завод построили на расстоянии 10 км
от А:
200 т ∙ 10 км + 100 т
∙ 50 км = 7000 т/км
Слайд 9
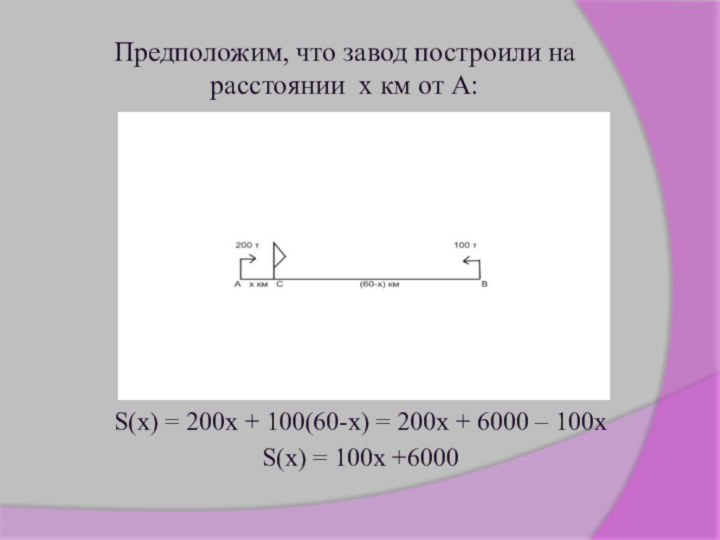
Предположим, что завод построили на расстоянии х км
от А:
S(x) = 200x + 100(60-x) = 200x +
6000 – 100x
S(x) = 100x +6000
Слайд 10
Линейная функция на отрезке от [0;60]
своё наименьшее значение принимает в точке x=0, т.е.
y min=6000, при x=0
Слайд 11
Количество тонно-километров,
пройденных транспортом от А до С за каждый день,
составляет 200х т/км, а от В до С – 100(60 – х) т/км. Суммарное количество тонно-километров выразится функцией
у=200х +100 (60 – х) = 100х + 6000, которая определена на отрезке [0; 60].
Исследуя функцию у min = 100х + 6000 на отрезке
[0; 60], получим у = 6000.
Эта линейная функция будет иметь минимальное
значение при х = 0, у min = 6000 т/км.
Вывод: Завод надо строить возле фермы А.
Слайд 12
Задача 2.
На дачных участках
нужно провести водопровод длиной 167 м. Имеются трубы длиной
5 м и 7 м. Сколько нужно использовать тех и других труб, чтобы сделать наименьшее количество соединений (трубы не резать)?
Слайд 13
Решение
Учитывая, что количество
как одних, так и других труб может изменяться, количество
7 – метровых труб обозначим через х, а 5 – метровых – через у. Тогда 7х – длина 7-метровых труб, 5у – длина 5-метровых труб. Отсюда получаем неопределенное уравнение 7х + 5у = 167
Выразив, например, переменную х через переменную у, получим: x = (167-5y) : 7
(1; 32), (6; 25), (11; 18), (16; 11), (21; 4).
Из этих решений наиболее выгодное последнее, т.е. х = 21, у = 4.
Вывод: Значит, надо взять 21 трубу по 7 метров и 4 трубы по 5 метров.
Слайд 14
Задача 3
Известно, что 1кг апельсинов содержит 150мг витамина
С, а 1кг яблок - 75 мг витамина С.
Сколько апельсинов и сколько яблок следует включить в дневной рацион питания, чтобы при минимальных затратах в нем оказалось 75 мг витамина С, не менее 0,25 кг апельсинов и не менее 0,25 кг яблок, если 1кг апельсинов стоит 60р., а 1кг яблок – 40р.?
Слайд 16
Ограничения имеют вид:
х ≥ 0,25
х
≥ 0,25 х ≥ 0,25
у ≥ 0,25 у ≥ 0,25 у ≥ 0,25
150х + 75у = 75 2х + у = 1 у = -2х +1
Целевая функция: F (х, у) = 60х + 40у
Необходимо найти такие х и у, при которых целевая функция принимает минимальное значение.
Построим область допустимых решений задачи:
Слайд 17
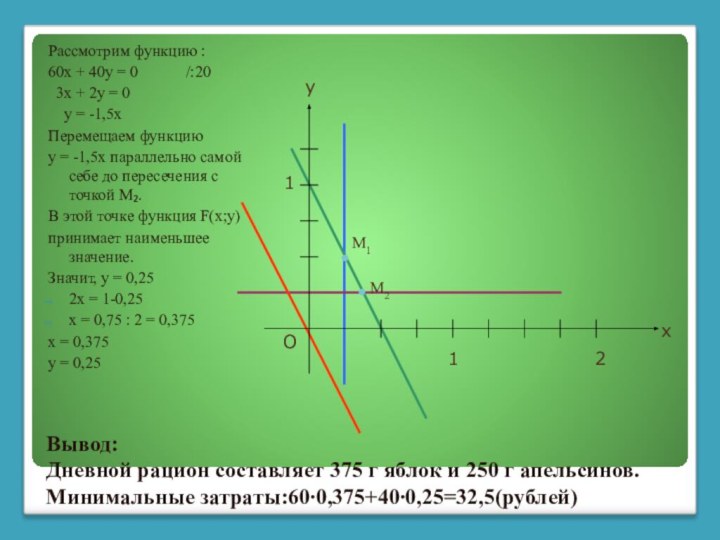
Вывод:
Дневной рацион составляет 375 г яблок и 250
г апельсинов.
Минимальные затраты:60∙0,375+40∙0,25=32,5(рублей)
Рассмотрим функцию :
60х + 40у = 0
/:20
3х + 2у = 0
у = -1,5х
Перемещаем функцию
у = -1,5х параллельно самой себе до пересечения с точкой М₂.
В этой точке функция F(х;у)
принимает наименьшее значение.
Значит, у = 0,25
2х = 1-0,25
х = 0,75 : 2 = 0,375
х = 0,375
у = 0,25
М1
М2
•
•
О
1
2
1
Слайд 18
Использование свойств квадратичной функции при решении экстремальных задач
Задача 4.
Окно имеет форму прямоугольника ,завершенного
полукругом. Периметр фигуры равен 6 м .Каковы должны быть размеры окна, чтобы окно пропускало наибольшее количество света?
Слайд 19
Окно будет обладать наибольшей пропускной способностью, если при
заданном периметре будет иметь максимальную площадь.
Пусть AB = x,
AD = y, тогда
P=AB+BC+AD+ DMC
6=x+2y+0,5 πx
у=3-х/2-(πх)/4
S=AB•BC+ (πx²) /8
S(x)=-(π/8 +1/2)x² +3x
Известно, что квадратный трехчлен принимает наибольшее значение при
x =-b/2a, т.е. x =12/(π+4), y= 6/ (π +4).
Ответ: Размеры окна 1,7×0,8







![Решение экономических задач и их применение с точки зрения оптимизации Линейная функция на отрезке от [0;60] своё наименьшее значение принимает](/img/tmb/7/618917/00a53967d251899a361880b4c45025c9-720x.jpg)