…un, соединенных знаком сложения.
Числа u1, u2, …un называются членами
ряда.Член un называется общим или n – ным членом ряда.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








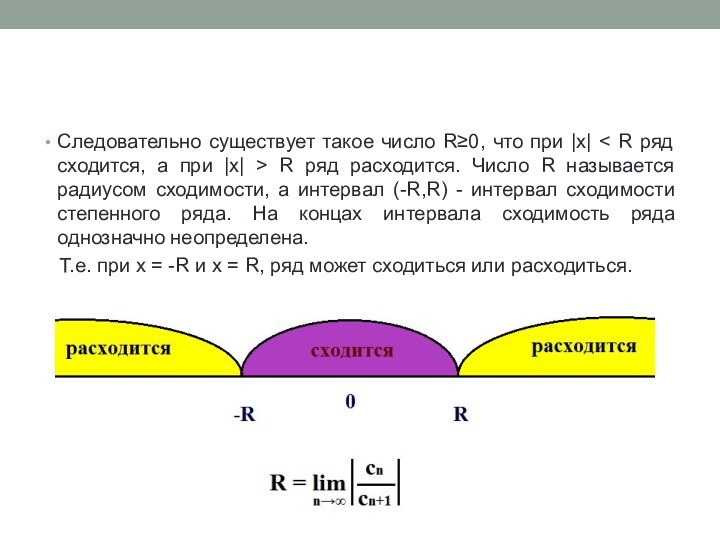
![Числовые ряды Если на отрезке [a,b], целиком принадлежащем интервалу сходимости (-R;R), функция f(x) является](/img/tmb/14/1305328/398ff210770f57b41b7397a272fc13ba-720x.jpg)




Свойства степенных рядов