- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ДЕМОНСТРАТИВНЫЕ УМОЗАКЛЮЧЕНИЯ(непосредственные умозаключения)
Содержание
- 2. План:Общая характеристика умозаключений.Превращение суждения.Обращение суждения. Противопоставление предикату.Умозаключения по логическому квадрату.
- 3. I. Общая характеристика умозаключений.Умозаключение – это форма
- 4. Посылки умозаключения - исходные суждения, из которых
- 5. «Преступление наказуемо» «Мошенничество – преступление» ___________________________________«Мошенничество наказуемо»
- 6. Все люди смертны.Сократ –человек.Сократ смертен
- 7. Виды умозаключенийПо строгости вывода:Демонстративные (необходимые)Недемонстративные (правдоподобные)
- 8. Виды умозаключенийПо направленности вывода:ДедуктивныеИндуктивныеУмозаключения по аналогии
- 9. Виды умозаключенийПо количеству посылок:НепосредственныеОпосредованные
- 10. Непосредственными (в традиционной логике) называются умозаключения из одной посылки, являющейся категорическим суждением.
- 11. II.Превращение суждения S есть РS не есть
- 12. Все S есть Р Ни одно S
- 13. Ни одно S не есть Р Все
- 14. Ни одно S не есть Р (Е)
- 15. Некоторые S есть Р (I) Некоторые S
- 16. Некоторые S не есть Р (О) Некоторые
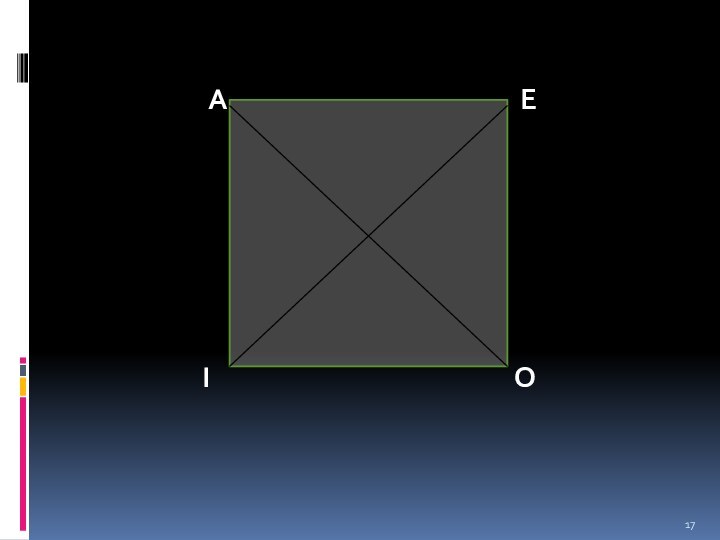
- 17. IOEA
- 18. III.Обращение суждения S есть Р P есть
- 19. Обращение подчиняется правилу: термин, нераспределенный в посылке, не может быть распределен в заключении.
- 20. Все S есть Р Некоторые Р
- 21. Ни одно S не есть Р Ни
- 22. Некоторые S есть Р Некоторые Р есть
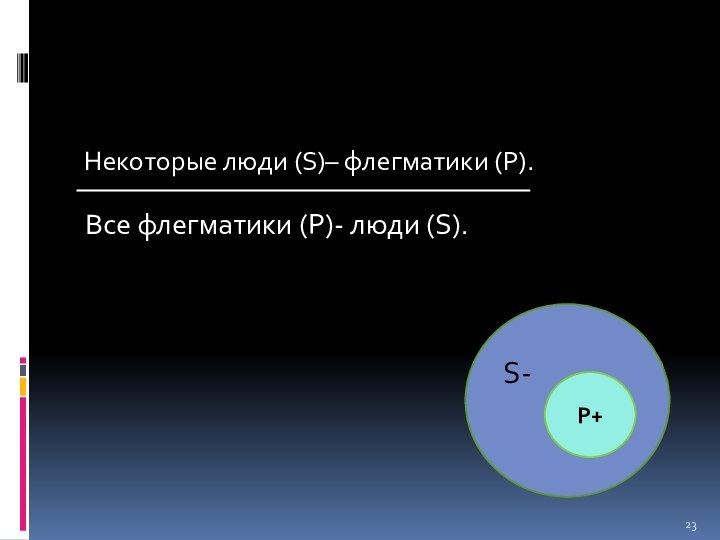
- 23. Некоторые люди (S)– флегматики (P).Все флегматики (P)- люди (S).
- 24. IV. Противопоставление предикату Все S есть
- 25. Взрослый человек (S) не помнит первых событий
- 26. Ни одно S не есть Р Некоторые
- 27. Некоторые S не есть Р (О) Некоторые
- 28. V. Умозаключения по логическому квадратуУмозаключения по логическому квадрату устанавливают взаимообусловленность истинностных значений суждений.
- 29. Выводы можно делать на основании отношения: - подчинения;- частичной совместимости; - противоречия;- противоположности.
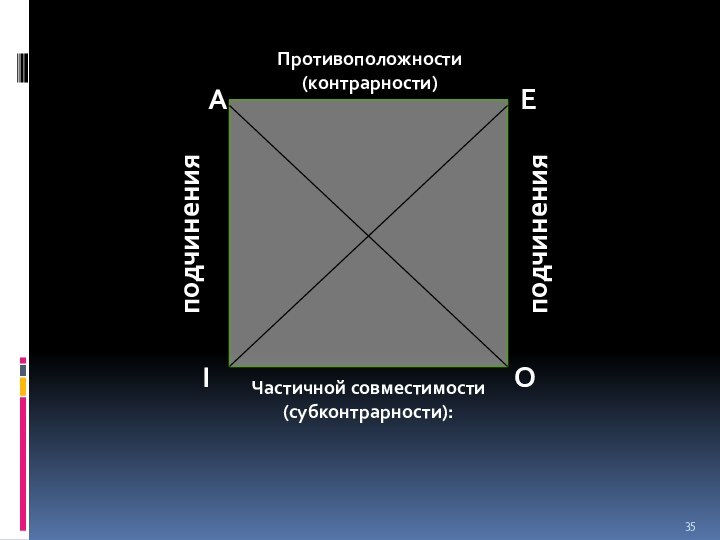
- 30. IOEAПротивоположности (контрарности)Частичной совместимости (субконтрарности): подчиненияподчиненияпротиворечия (контрадикторности)
- 31. Отношение противоречия (контрадикторности): из истинности одного суждения
- 32. Отношение противоположности (контрарности):из истинности одного суждения следует
- 33. Отношение частичной совместимости (субконтрарности):из ложности одного суждения
- 34. Отношение подчинения:из истинности подчиняющего суждения следует истинность
- 35. Скачать презентацию
- 36. Похожие презентации
План:Общая характеристика умозаключений.Превращение суждения.Обращение суждения. Противопоставление предикату.Умозаключения по логическому квадрату.






























Слайд 2
План:
Общая характеристика умозаключений.
Превращение суждения.
Обращение суждения.
Противопоставление предикату.
Умозаключения по
логическому квадрату.
Слайд 3
I. Общая характеристика умозаключений.
Умозаключение – это форма мышления,
посредством которой из одного или нескольких суждений выводится новое
суждение.Слайд 4 Посылки умозаключения - исходные суждения, из которых выводится
новое суждение.
Заключение - новое суждение, полученное логическим путем
из посылок. Логический переход от посылок к заключению называется выводом.
Слайд 5
«Преступление наказуемо»
«Мошенничество – преступление»
___________________________________
«Мошенничество наказуемо»
Слайд 7
Виды умозаключений
По строгости вывода:
Демонстративные (необходимые)
Недемонстративные (правдоподобные)
Слайд 10 Непосредственными (в традиционной логике) называются умозаключения из одной
посылки, являющейся категорическим суждением.
Слайд 11
II.Превращение суждения
S есть Р
S не есть не-Р
Превращение –
преобразование суждения в суждение, противоположное по качеству с предикатом,
противоречащим предикату исходного суждения.Слайд 12 Все S есть Р Ни одно S не есть
не-Р
Все (количество) справедливые решения (S) являются (связка) одобряемыми людьми
(Р).____________________________________
Ни одно (количество) справедливое решение (S) не является (связка) неодобряемым людьми (не-Р).
Слайд 13 Ни одно S не есть Р Все S есть
не-Р
Ни одна захватническая война (S) не является справедливой (Р);
(Е)___________________________________
Все захватнические войны (S) являются несправедливыми (не-Р); (А)
Слайд 14 Ни одно S не есть Р (Е) Все S
есть не-Р (А)
Человек (S) не рождается с развитым воображением
(P).Человек (S)рождается с неразвитым воображением (не P).
Слайд 15 Некоторые S есть Р (I) Некоторые S не есть
не-Р (О)
Некоторые металлы (S) являются жидкими (Р)
____________________________________Некоторые металлы(S) не являются не-жидкими (не-Р).
Слайд 16 Некоторые S не есть Р (О) Некоторые S есть
не-Р (I)
Некоторые студенты (S)не являются отличниками.
___________________________________
Некоторые
студенты (S)являются не-отличниками (не-Р).
Слайд 18
III.Обращение суждения
S есть Р
P есть S
Обращение –
преобразование суждения, в результате которого S исходного суждения становится
P, а предикат субъектом заключения.
Слайд 19
Обращение подчиняется правилу:
термин, нераспределенный в посылке, не
может быть распределен в заключении.
Слайд 20
Все S есть Р
Некоторые Р есть S
Все
фильмы Тарковского (S+) есть киношедевры (Р-) (А)
___________________________________
Некоторые
киношедевры (Р-) есть фильмы Тарковского (I-)Слайд 21 Ни одно S не есть Р Ни одно Р
не есть S
«Ни один студент первой группы (S+) не
является неуспевающим (Р+)» (Е) ___________________________________
«Ни один неуспевающий (Р+) не является студентом первой группы (S+)» (Е)
Слайд 22
Некоторые S есть Р
Некоторые Р есть S
Например суждение
:
«Некоторые спортсмены (S-) – аспиранты (Р-) (I)
______________________________________________обращается в суждение:
«Некоторые аспиранты (Р-) – спортсмены (S-)» (I).
Слайд 24 IV. Противопоставление предикату Все S есть Р (А) Ни одно
не-Р не есть S (Е)
Все современные физики (S) знают
имя Ньютона (Р) (А)___________________________________________
Ни один человек, не знающий имени Ньютона (не-Р), не является современным физиком (S) (Е).
Слайд 25 Взрослый человек (S) не помнит первых событий жизни
(P).
Некоторые из непомнящих первые события жизни (не P) являются
взрослыми людьми (S).Слайд 26 Ни одно S не есть Р Некоторые не-Р есть
S
«Несоблюдение принципа разделения властей не остается незамеченным СМИ»
______________________________________«Среди фактов, которые отмечаются в СМИ, есть случаи несоблюдения принципа разделения властей»
Слайд 27 Некоторые S не есть Р (О) Некоторые не-Р есть
S (I)
Некоторые свидетели не являются совершеннолетними
_______________________________________
Некоторые
несовершеннолетние являются свидетелями.
Слайд 28
V. Умозаключения по логическому квадрату
Умозаключения по логическому квадрату
устанавливают взаимообусловленность истинностных значений суждений.
Слайд 29
Выводы можно делать на основании отношения:
- подчинения;
-
частичной совместимости;
- противоречия;
- противоположности.
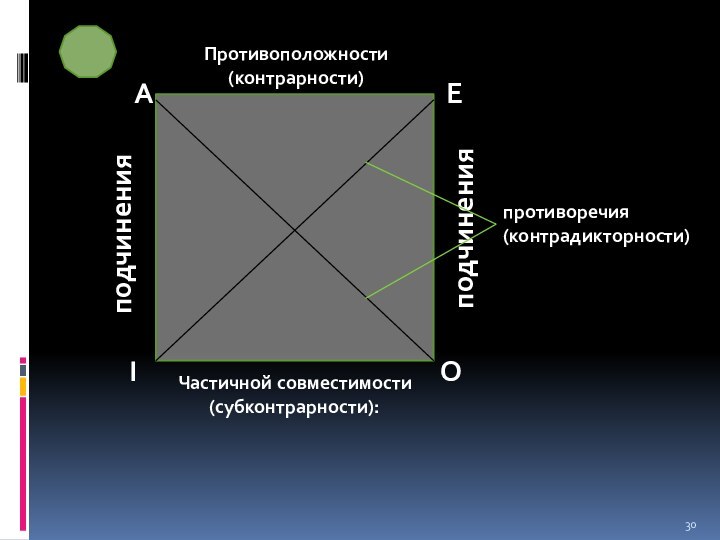
Слайд 30
I
O
E
A
Противоположности (контрарности)
Частичной совместимости (субконтрарности):
подчинения
подчинения
противоречия (контрадикторности)
Слайд 31
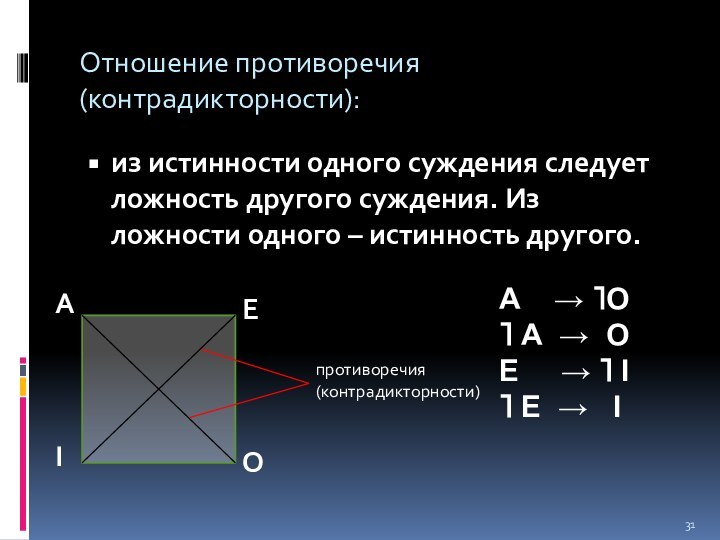
Отношение противоречия (контрадикторности):
из истинности одного суждения следует
ложность другого суждения. Из ложности одного – истинность другого.
А → ⌉О
⌉ А → О
Е → ⌉ I
⌉ Е → I
противоречия (контрадикторности)
I
A
O
E
Слайд 32
Отношение противоположности (контрарности):
из истинности одного суждения следует ложность
другого суждения, но из ложности одного из них не
следует истинность другого.А→⌉ Е;
Е→⌉ А;
⌉ А→ (Е ⌉ Е);
⌉ Е→ (А ⌉А).
I
O
E
A
противоположности (контрарности):
Слайд 33
Отношение частичной совместимости (субконтрарности):
из ложности одного суждения следует
истинность другого, но из истинности одного из них может
следовать как истинность, так и ложность другого суждения.⌉I → О
⌉ О →I
I → (О ⌉ О)
О→ ( I ⌉ I)
Частичной совместимости (субконтрарности):
A
E
I
O
Слайд 34
Отношение подчинения:
из истинности подчиняющего суждения следует истинность подчиненного
суждения, но не наоборот. Из истинности подчиненного суждения истинность
подчиняющего не следует, оно может быть истинным, но может быть и ложным.А →I;
Е → О;
I → (А ⌉ А);
О → (Е ⌉ Е);
⌉I → ⌉А;
⌉О →⌉ Е;
⌉А → (I ⌉ I );
⌉Е → (О ⌉ О).





























