Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Дисперсия вариационного ряда и её свойства

Содержание

ОпределениеДисперсией вариационного рядя называется средняя арифметическая квадратов отклонений вариантов от их среднейСредним квадратическим отклонением называется арифметическое отклонение значение корня квадратного из дисперсии
Дисперсия вариационного ряда и её свойстваЗанятие 8 ОпределениеДисперсией вариационного рядя называется средняя арифметическая квадратов отклонений вариантов Дисперсия и среднее квадратическое отклонение – мера рассеянияИспользуется при сравнительных статистических исследованиях, Правило трёх (характерно для нормального распределения) Вычислить дисперсию и среднее квадратичное отклонениеРаспределение рабочих предприятия по времени, затрачиваемому на обработку одной детали Свойства дисперсийТеорема 1. Если все варианты увеличить (уменьшить) в k раз, то Свойства дисперсийТеорема 2. Если варианты увеличить или уменьшить на одну и ту Свойства дисперсийТеорема 3. Если веса увеличить или уменьшить в одно и то Свойства дисперсийТеорема 4. Дисперсия равна средней арифметической квадратов вариантов на соответствующие им Совокупность разбита на l непересекающихся группГрупповой дисперсией , ОпределенияМежгрупповой дисперсией называется средняя арифметическая квадратов отклонений групповых средних всех непересекающихся ОпределенияСредней групповых дисперсий называется средняя арифметическая групповых дисперсий, т.е.где - объем непересекающихся групп. Свойства дисперсийДисперсия распределения членов всей совокупности относительно общей средней называется общей дисперсией.Теорема Определение Отношение среднего квадратичного отклонения к средней величине признака, вычисленное в процентах, называется коэффициентом вариации: Пример. Вычислить межгрупповую дисперсию распределения рабочих по заработной плате по цехам. РешениеВычислим среднюю заработную плату рабочих цеха № 1. Для этого переходим к соответствующему дискретному распределению. РешениеАналогично вычисляем средние групповые для цеха № 2 и № 3 – Моменты вариационного рядаМоментом k-го порядка варьирующего признака X по отношению к Моменты вариационного рядаЕсли а = 0, момент называется начальным ОпределенияЗа показатель отклонения распределения признака X от симметрии относительно X принимают величинуназываемую асимметрией ОпределенияЭксцессом называют величинуОн показывает степень крутости кривой распределения признака X по сравнению Замечание Если , то распределение нормальное. Если ЗамечаниеОшибки асимметрии и эксцесса вычисляются соответственно по формулам: СПАСИБО ЗА ВНИМАНИЕ
Слайды презентации

Слайд 2 Определение
Дисперсией вариационного рядя называется средняя

ОпределениеДисперсией вариационного рядя называется средняя арифметическая квадратов отклонений вариантов от

арифметическая квадратов отклонений вариантов от их средней



Средним квадратическим отклонением


называется арифметическое отклонение значение корня квадратного из дисперсии

Слайд 3 Дисперсия и среднее квадратическое отклонение – мера рассеяния
Используется

Дисперсия и среднее квадратическое отклонение – мера рассеянияИспользуется при сравнительных статистических

при сравнительных статистических исследованиях, для обоснования ошибки репрезентативности выборочного

наблюдения, а также при изучении корреляционных и иных статистических связей между признаками фактора и признаками следствия, или между причиной и следствием.
Среднее квадратическое отклонение позволяет правильно оценить надежность выборочных показателей.

Слайд 4 Правило трёх (характерно для нормального распределения)

Правило трёх (характерно для нормального распределения)

Слайд 5 Вычислить дисперсию и среднее квадратичное отклонение
Распределение рабочих предприятия

Вычислить дисперсию и среднее квадратичное отклонениеРаспределение рабочих предприятия по времени, затрачиваемому на обработку одной детали

по времени, затрачиваемому на обработку одной детали








Слайд 6 Свойства дисперсий
Теорема 1.
Если все варианты увеличить (уменьшить)

Свойства дисперсийТеорема 1. Если все варианты увеличить (уменьшить) в k раз,

в k раз, то дисперсия увеличится (уменьшится) в раз,

а среднее квадратическое отклонение - в раз.



где - средняя арифметическая, - дисперсия вариационного ряда.


Слайд 7 Свойства дисперсий
Теорема 2.
Если варианты увеличить или уменьшить

Свойства дисперсийТеорема 2. Если варианты увеличить или уменьшить на одну и

на одну и ту же постоянную величину, то дисперсия

не изменится.


Слайд 8 Свойства дисперсий
Теорема 3.
Если веса увеличить или уменьшить

Свойства дисперсийТеорема 3. Если веса увеличить или уменьшить в одно и

в одно и то же число раз, то дисперсия

не изменится.

Слайд 9 Свойства дисперсий
Теорема 4.
Дисперсия равна средней арифметической квадратов

Свойства дисперсийТеорема 4. Дисперсия равна средней арифметической квадратов вариантов на соответствующие

вариантов на соответствующие им веса без квадрата средней арифметической,

т.е.


Слайд 10 Совокупность разбита на l непересекающихся групп
Групповой дисперсией

Совокупность разбита на l непересекающихся группГрупповой дисперсией , называется дисперсия

, называется дисперсия распределения членов j -ой

группы относительно их средней – т.е. групповой средней



где - частоты вариантов в группе,

- объем группы.

Слайд 11 Определения
Межгрупповой дисперсией называется средняя арифметическая квадратов отклонений

ОпределенияМежгрупповой дисперсией называется средняя арифметическая квадратов отклонений групповых средних всех непересекающихся

групповых средних всех непересекающихся групп от общей средней

, т.е.




где - объемы групп.

Слайд 12 Определения
Средней групповых дисперсий называется средняя арифметическая групповых дисперсий,

ОпределенияСредней групповых дисперсий называется средняя арифметическая групповых дисперсий, т.е.где - объем непересекающихся групп.

т.е.




где - объем непересекающихся групп.

Слайд 13 Свойства дисперсий
Дисперсия распределения членов всей совокупности относительно общей

Свойства дисперсийДисперсия распределения членов всей совокупности относительно общей средней называется общей

средней называется общей дисперсией.
Теорема 5 (правило сложения дисперсий).
Общая

дисперсия равна сумме средней групповых дисперсий непересекающихся групп, на которые разбита совокупность, и межгрупповой дисперсии , т.е.

Слайд 14 Определение
Отношение среднего квадратичного отклонения к средней величине

Определение Отношение среднего квадратичного отклонения к средней величине признака, вычисленное в процентах, называется коэффициентом вариации:

признака, вычисленное в процентах, называется коэффициентом вариации:

Слайд 15 Пример. Вычислить межгрупповую дисперсию распределения рабочих по заработной

Пример. Вычислить межгрупповую дисперсию распределения рабочих по заработной плате по цехам.

плате по цехам.

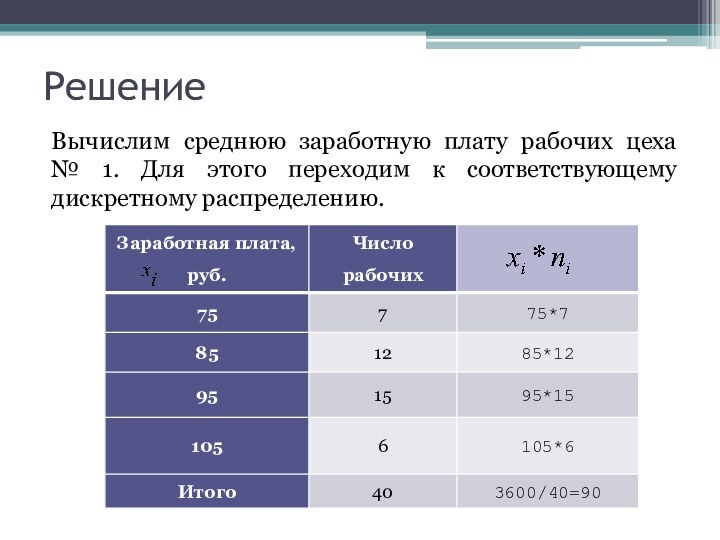
Слайд 16 Решение
Вычислим среднюю заработную плату рабочих цеха № 1.

РешениеВычислим среднюю заработную плату рабочих цеха № 1. Для этого переходим к соответствующему дискретному распределению.

Для этого переходим к соответствующему дискретному распределению.

Слайд 17 Решение
Аналогично вычисляем средние групповые для цеха № 2

РешениеАналогично вычисляем средние групповые для цеха № 2 и № 3

и № 3 – 105 и 115 соответственно.
Вычисляем общую

среднюю – это средняя заработная плата всех рабочих предприятия


В соответствии с формулой вычисления межгрупповой дисперсии, получаем

Слайд 18 Моменты вариационного ряда
Моментом k-го порядка варьирующего признака

Моменты вариационного рядаМоментом k-го порядка варьирующего признака X по отношению к

X по отношению к значению а называют среднее математическое

из k-х степеней отклонений значений признака от а, т. е.

Слайд 19 Моменты вариационного ряда
Если а = 0, момент называется

Моменты вариационного рядаЕсли а = 0, момент называется начальным ,

начальным , а при

его называют центральным .

Слайд 20 Определения
За показатель отклонения распределения признака X от симметрии

ОпределенияЗа показатель отклонения распределения признака X от симметрии относительно X принимают величинуназываемую асимметрией

относительно X принимают величину




называемую асимметрией

Слайд 21 Определения
Эксцессом называют величину




Он показывает степень крутости кривой распределения

ОпределенияЭксцессом называют величинуОн показывает степень крутости кривой распределения признака X по

признака X по сравнению с крутостью нормального распределения дисперсия

которого равна .


Слайд 22 Замечание
Если , то распределение

Замечание Если , то распределение нормальное. Если , то

нормальное.
Если , то крутость положительная и

кривая распределения имеет более острую вершину, чем при нормальном распределении.
Если , то крутость отрицательная и кривая имеет более плоскую вершину. Возможно даже, что в центре распределения будут выемки (двухмодальная кривая).
Значения эксцесса лежат на полусегменте .

Слайд 23 Замечание
Ошибки асимметрии и эксцесса вычисляются соответственно по формулам:

ЗамечаниеОшибки асимметрии и эксцесса вычисляются соответственно по формулам:
  • Имя файла: dispersiya-variatsionnogo-ryada-i-eyo-svoystva.pptx
  • Количество просмотров: 139
  • Количество скачиваний: 0
- Предыдущая Пищеварение, витамины, питательные вещества
Следующая - Кошка в моём доме

Похожие презентации

Греческие боги Греческие боги 153
Технологии и методы реализации компетентностного подхода в обучении Технологии и методы реализации компетентностного подхода в обучении 107
Организация совместных мероприятий с родителями как одна из форм работы взаимодействия ДОУ и семьи проект (младшая группа) Организация совместных мероприятий с родителями как одна из форм работы взаимодействия ДОУ и семьи проект (младшая группа) 121
МСФО (ifrs) 5 Долгосрочные активы, предназначенные для продажи, и прекращенная деятельность МСФО (ifrs) 5 Долгосрочные активы, предназначенные для продажи, и прекращенная деятельность 116
ТО и ТР карбюраторных двигателей ТО и ТР карбюраторных двигателей 85
Арабо-мусульманская средневековая философия Арабо-мусульманская средневековая философия 106
Экологический проект. материал (младшая группа) по теме Экологический проект. материал (младшая группа) по теме 106
Шаблоны презентаций Радужные Шаблоны презентаций Радужные 122
Heineken case study Heineken case study 105
Картотека дидактических игр для развития познавательных способностей презентация Картотека дидактических игр для развития познавательных способностей презентация 126
Слайдовая презентация Слайдовая презентация 143
progulka v detskom sadu 2 chast progulka v detskom sadu 2 chast 100
Презентация опыта работы для конкурса Воспитатель года - 2016 презентация Презентация опыта работы для конкурса Воспитатель года - 2016 презентация 91
Понятие о лекарствах. Понятие о лекарствах. 103
Микроскопическое исследование осадка мочи Микроскопическое исследование осадка мочи 108
Естественное и механическое движение населения Естественное и механическое движение населения 106
Системно-деятельностный подход презентация к уроку Системно-деятельностный подход презентация к уроку 103
svoya igra 5 klass svoya igra 5 klass 192
Особенности работы в группах для детей со сложным дефектом Особенности работы в группах для детей со сложным дефектом 110
Презентация по окружающему миру Природные зоны суши Земли Презентация по окружающему миру Природные зоны суши Земли 61
ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ 97
master-klass master-klass 85
98
Презентация А то ли мы едим. Презентация А то ли мы едим. 159
презентация жди меня презентация к уроку (старшая группа) презентация жди меня презентация к уроку (старшая группа) 103
Пример поиска информации на государственных образовательных порталах. Поисковые системы. Пример поиска информации на государственных образовательных порталах. Поисковые системы. 130
Мультимедийная игра Путешествие в мир полезных продуктов презентация к уроку (средняя группа) Мультимедийная игра Путешествие в мир полезных продуктов презентация к уроку (средняя группа) 38
Подготовка к ГИА и ЕГЭ Подготовка к ГИА и ЕГЭ 87
М.Ю.Лермонтов. М.Ю.Лермонтов. 99
Презентация по воспитательной работе Жизнь и творчество Роберта Рождественского Презентация по воспитательной работе Жизнь и творчество Роберта Рождественского 146