- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Доверительный интервал для среднего
Содержание
- 2. План:Точечные и интервальные оценкиДИ для среднего при известной дисперсииДИ для среднего при неизвестной дисперсии
- 3. Точечная оценка (point estimate)Точечной оценкой называется число,
- 4. Ошибка оценки (estimation error)разность между оцениваемым параметром
- 5. Критерии точечных оценокНесмещенность оценки означает, что ее
- 6. Доверительный интервал (confidence interval)Доверительный интервал – вычисленный
- 7. Доверительная вероятностьДоверительная вероятность (или уровень доверия, confidence
- 8. Для нормального распределения…Значение нормально распределенного признака находится
- 9. Форма записи доверительного интервалаВариант 1. «Мы на
- 10. Зависимость от выборкиДоверительные интервалы, построенные для 15
- 11. Описание проблемы случай: σ известна или
- 12. Метод1. В качестве точечной оценки среднего генеральнойсовокупности
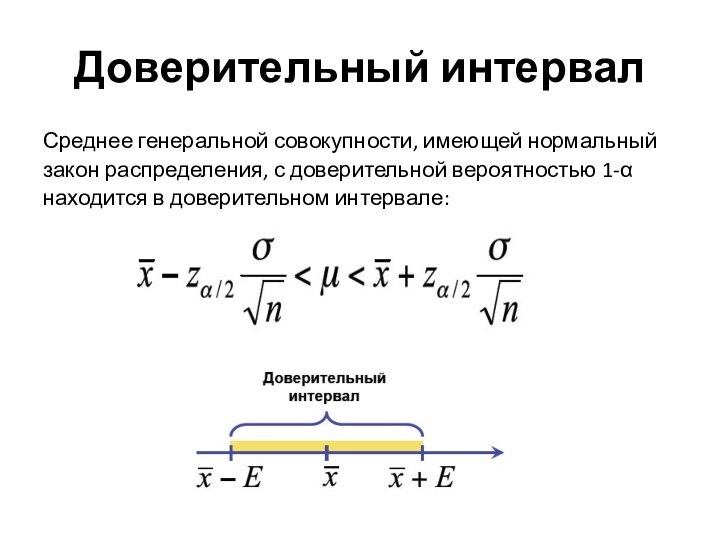
- 13. Доверительный интервалСреднее генеральной совокупности, имеющей нормальныйзакон распределения,
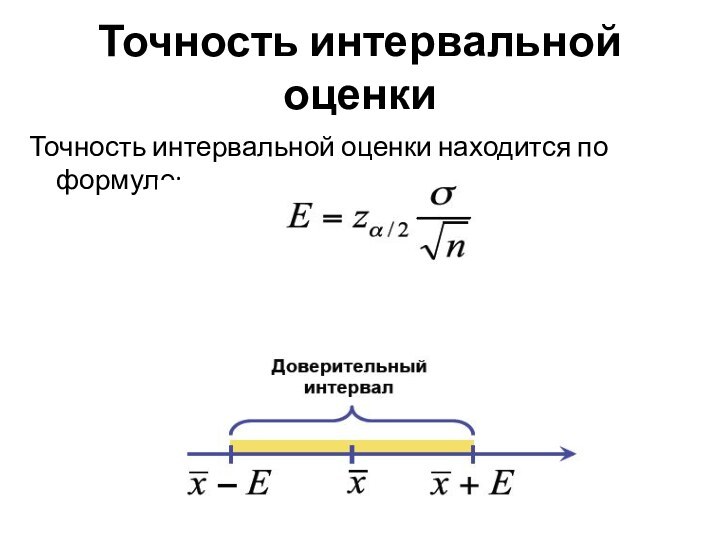
- 14. Точность интервальной оценкиТочность интервальной оценки находится по формуле:
- 15. Последовательность действийШаг 1. По выборке вычислить выборочное
- 16. Важное замечаниеЕсли значение σ неизвестно и при
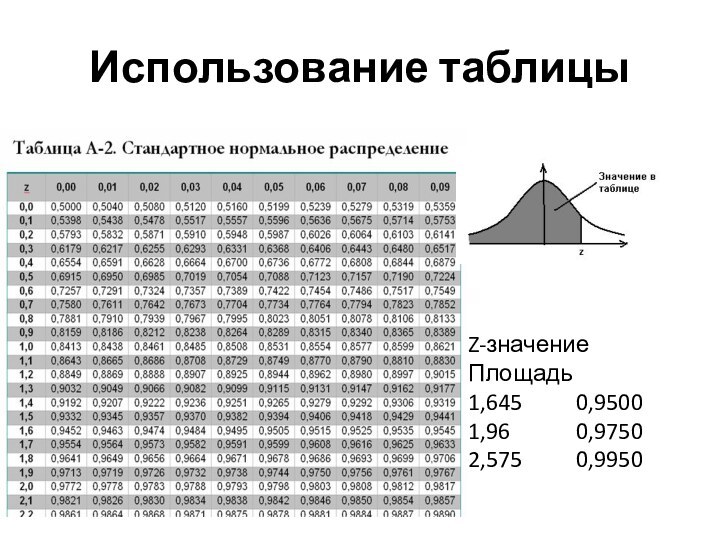
- 17. Использование таблицыZ-значение Площадь1,645 0,95001,96 0,97502,575 0,9950
- 18. Самые используемые z-значения
- 19. ПримерРектор университета хочет узнать, каков средний возраст
- 20. РешениеШаг 1. По выборке вычислено выборочное среднее
- 21. Объем выборки для оценки среднегоФормула для нахождения
- 22. ПримерДекан просит преподавателя по статистике оценить средний
- 23. Решение
- 24. Описание проблемы σ неизвестно и n≤30Цель. Оценить
- 25. Отличие методаПри построении доверительного интервала вместо нормального
- 26. Число степеней свободыЧисло степеней свободы – это
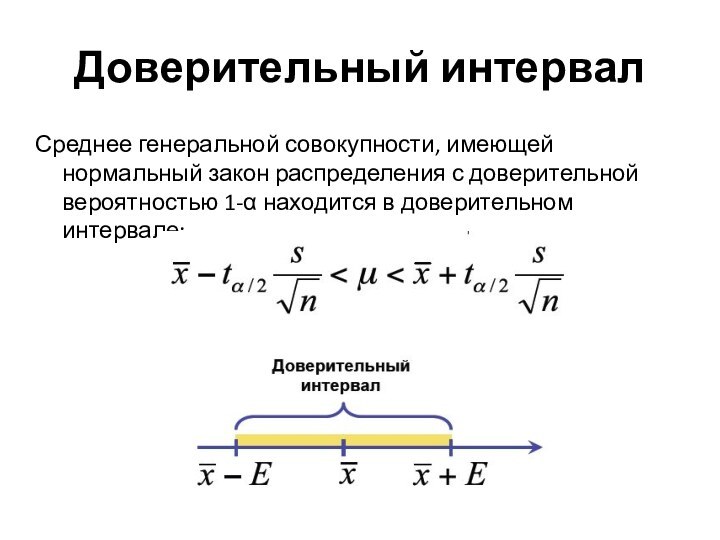
- 27. Доверительный интервалСреднее генеральной совокупности, имеющей нормальный закон распределения с доверительной вероятностью 1-α находится в доверительном интервале:
- 28. Последовательность действий
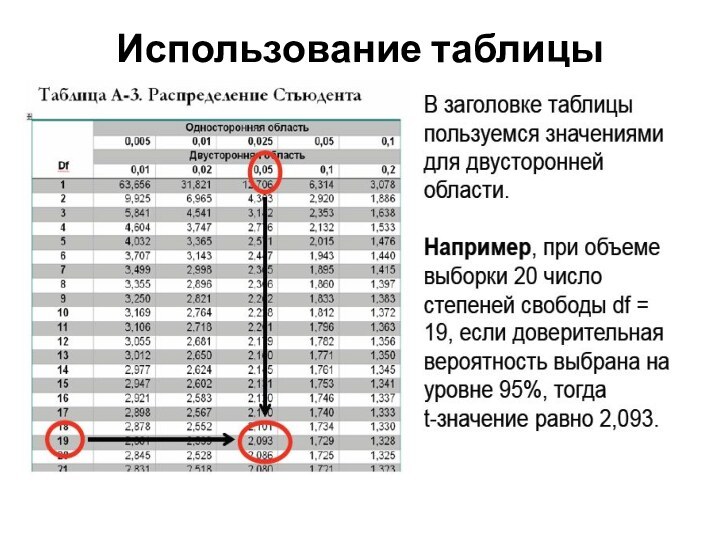
- 29. Использование таблицы
- 30. ЗадачаУ 20 студентов, сдававших выпускной экзамен, сердце
- 31. Скачать презентацию
- 32. Похожие презентации
План:Точечные и интервальные оценкиДИ для среднего при известной дисперсииДИ для среднего при неизвестной дисперсии






















Слайд 3
Точечная оценка (point estimate)
Точечной оценкой называется число, которое
используется в качестве оценки параметра генеральной совокупности.
Например, среднее значение
выборки является точечной оценкой среднего значения генеральной совокупности. Доля признака, рассчитанная по выборке, может рассматриваться как оценка доли признака в генеральной совокупности.μ
Оценка Параметр
Слайд 4
Ошибка оценки (estimation error)
разность между оцениваемым параметром генеральной
совокупности и оценкой, рассчитанной на основе выборки. Ошибка оценки
обычно неизвестна, поскольку неизвестен параметр.Ошибка оценки = Параметр – Оценка
Слайд 5
Критерии точечных оценок
Несмещенность оценки означает, что ее математическое
ожидание
равно значению оцениваемого параметра
генеральной совокупности.
Эффективность оценки означает, что статистика,
используемая
в качестве точечной оценки параметрагенеральной совокупности имеет минимальную стандартную
ошибку.
Состоятельность оценки означает, что по мере увеличения
объема выборки ее значение приближается к значению
оцениваемого параметра генеральной совокупности.
Слайд 6
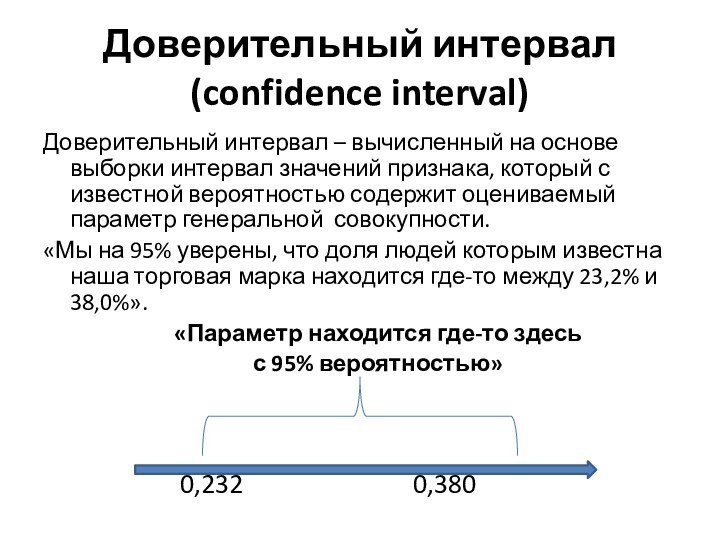
Доверительный интервал (confidence interval)
Доверительный интервал – вычисленный на
основе выборки интервал значений признака, который с известной вероятностью
содержит оцениваемый параметр генеральной совокупности.«Мы на 95% уверены, что доля людей которым известна наша торговая марка находится где-то между 23,2% и 38,0%».
«Параметр находится где-то здесь
с 95% вероятностью»
0,232 0,380
Слайд 7
Доверительная вероятность
Доверительная вероятность (или уровень доверия, confidence level)
– это вероятность того, что доверительный интервал содержит значение
оцениваемого параметра.Доверительную вероятность принято устанавливать на уровнях 90%, 95% и 99%. Чем выше доверительная вероятность, тем более широкий и менее полезный интервал мы получим.
90% 95% 99%
Используется наиболее часто
Слайд 8
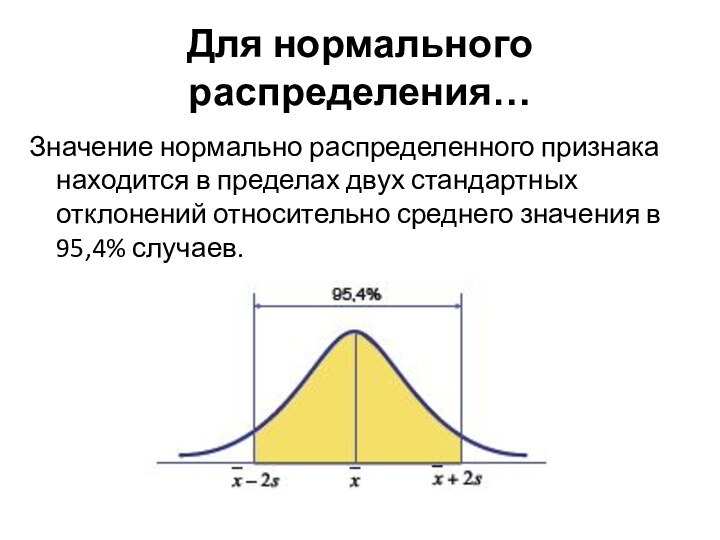
Для нормального распределения…
Значение нормально распределенного признака находится в
пределах двух стандартных отклонений относительно среднего значения в 95,4%
случаев.
Слайд 9
Форма записи доверительного интервала
Вариант 1. «Мы на 95%
уверены, что среднее значение роста студентов находится где-то между
165 и 175 см».Вариант 2. Среднее значение μ генеральной совокупности
находится в интервале от 165 до 175 с доверительной
вероятностью 0,95.
Вариант 3. При помощи формулы:
Р (165<μ<175) = 0,95
Слайд 10
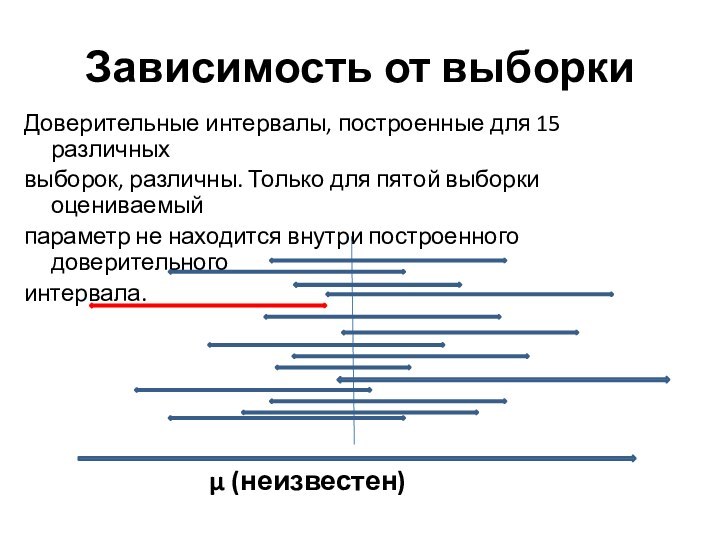
Зависимость от выборки
Доверительные интервалы, построенные для 15 различных
выборок,
различны. Только для пятой выборки оцениваемый
параметр не находится внутри
построенного доверительногоинтервала.
μ (неизвестен)
Слайд 11
Описание проблемы
случай: σ известна или n≥30
Цель. Оценить среднее
для генеральной совокупности,
имеющей нормальный закон распределения с параметрами μ,
σ.Что мы имеем. Имеем случайную выборку объема n из
генеральной совокупности. Стандартное отклонение σ
предполагается известным или объем выборки n≥30.
Требуется. Построить доверительный интервал для среднего:
х - Е < μ < х + Е
Слайд 12
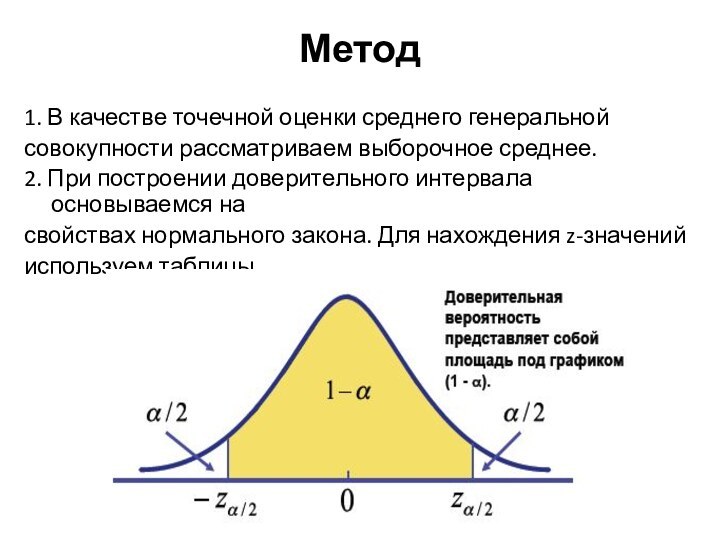
Метод
1. В качестве точечной оценки среднего генеральной
совокупности рассматриваем
выборочное среднее.
2. При построении доверительного интервала основываемся на
свойствах нормального
закона. Для нахождения z-значенийиспользуем таблицы.
Слайд 13
Доверительный интервал
Среднее генеральной совокупности, имеющей нормальный
закон распределения, с
доверительной вероятностью 1-α
находится в доверительном интервале:
Слайд 15
Последовательность действий
Шаг 1. По выборке вычислить выборочное среднее.
Шаг
2. По таблице нормального закона найти z-значение для
доверительной вероятности
1 - α.Шаг 3. Вычислить точность интервальной оценки по формуле:
Шаг 4. Подставить полученные значения в формулу для
доверительного интервала:
Шаг 5. Написать ответ.
х - Е < μ < х + Е
Слайд 16
Важное замечание
Если значение σ неизвестно и при этом
объем выборки n≥30,
тогда вместо σ используем выборочное стандартное отклонение
s:
Слайд 19
Пример
Ректор университета хочет узнать, каков средний возраст студентов,
обучающихся в настоящее время.
Из предыдущих исследований известно, что стандартное
отклонение равно 2 годам. Сделана выборка из 50 студентов и вычислено среднее. Оно оказалось равно 20,3 года.Найти 95%-ый доверительный интервал для генерального среднего.
Слайд 20
Решение
Шаг 1. По выборке вычислено выборочное среднее 20,3.
Шаг
2. Доверительная вероятность 95% соответствует z-
значению 1,96.
Шаг 3. Вычислим
точность интервальной оценки по формуле:Шаг 4. Подставим полученные значения в формулу для
доверительного интервала:
Шаг 5. Напишем ответ: 19, 75 < μ<20,85
Слайд 21
Объем выборки для оценки среднего
Формула для нахождения точности
оценки:
Выражаем объем выборки:
Если известны E, σ и доверительная вероятность,
то по этой формуле подсчитывается минимальный объем выборки, который необходим для построения интервальной оценки.
Слайд 22
Пример
Декан просит преподавателя по статистике оценить средний возраст
студентов факультета.
Какого размера выборка необходима?
Преподаватель статистики считает, что оценка
должна быть сделана с точностью до 1 года и с вероятностью 99%.Из ранее проведенного исследования известно, что стандартное отклонение возраста – 2 года.
Слайд 24
Описание проблемы
σ неизвестно и n≤30
Цель. Оценить среднее для
генеральной совокупности,
имеющей нормальный закон распределения с параметрами μ, σ.
Что
мы имеем. Имеем случайную выборку объема n из генеральной совокупности. Стандартное отклонение σ неизвестно и объем выборки n≤30.Требуется. Построить доверительный интервал для среднего:
х - Е < μ < х + Е
Слайд 25
Отличие метода
При построении доверительного интервала вместо нормального распределения
используем распределение Стьюдента.
Для нахождения t-значений будем использовать таблицы распределения
Стьюдента.
Слайд 26
Число степеней свободы
Число степеней свободы – это количество
значений, которые
могут свободно изменяться после того, как по выборке
быловычислено значение статистики.
Например, пусть известно, что среднее для выборки из пяти
значений оказалось равно 10. Тогда четыре из пяти значений
могут изменяться, а пятое всегда определено, поскольку сумма
пяти есть 50. Число степеней свободы в этом случае: 5 – 1 = 4.
Обозначение: df (degrees of freedom).
Нахождение. Число степеней свободы при построении
доверительного интервала для среднего: df = n – 1.
Слайд 27
Доверительный интервал
Среднее генеральной совокупности, имеющей нормальный закон распределения
с доверительной вероятностью 1-α находится в доверительном интервале:
Слайд 30
Задача
У 20 студентов, сдававших выпускной экзамен, сердце билось
в среднем со скоростью 96 ударов в минуту.
Стандартное отклонение
выборки было равно 5 ударам в минуту.Найти 95%-ый доверительный интервал для генерального среднего.





























