Слайд 2
Природа электрического тока в металлах
Опыт Рикке
+
ток 1 год
До
опытов Рикке было хорошо известно, что ток в жидкостях
и газе связан с перено- сом вещества. Целью данного эксперимента
было выяснение вопроса – существует ли хотя бы в малейшей степени перенос вещества при прохождении тока по металлу.
С этой целью Рикке взял три цилиндра с тщательно отполированными торцами, составил из них электрическую цепь, как это показано на рисунке,
и пропускал по этой цепи ток в одном направлении в течение длительного времени (1 год). Затем он разобрал цепь и тщательно исследовал под микроскопом торцы, находившиеся в контакте друг с другом.
Cu
Cu
Al
Слайд 3
Результаты эксперимента
Оказалось, что на контактирующих торцах цилиндров
не
обнаружено следов другого металла
Вывод
Прохождение электрического тока по металлу не
связано с
переносом вещества
Слайд 4
Опыт Стюарта и Толмена
Носители электрического тока в металлах
являются
свободными в том смысле, что при сколь угодно малом
напряжении в проводнике возникает ток
(механическая аналогия – брусок, лежащий на Земле сдвинется с места начиная только
с определенной величины силы. Большой корабль при отсутствии ветра и течения можно
сдвинуть с места одним мизинцем)
Идея эксперимента
Если проводник разогнать до большой скорости и затем резко
затормозить, то носители заряда продолжат движение по
инерции, и в цепи должен возникнуть кратковременный ток
Слайд 5
«Водяная» аналогия
При резком торможении тележки вода продолжает
свое
движение по инерции и выливается из кузова тележки
Слайд 6
удалось определить отношение . Оно оказалось равным 1,8·1011
Кл/кг. Эта величина совпадает с отношением заряда электрона к
его массе, найденным ранее из других опытов.
Слайд 7
Классическая теория проводимости металлов
Друде и Лорентц предложили рассматривать
электроны в
металле как свободный газ.
Скорость теплового хаотического
движения свободных
электронов определяется соотношением:
где m – масса электрона, m=9,1∙10-31 кг
V – скорость теплового движения
k- постоянная Больцмана, k=
Т – абсолютная температура
При комнатной температуре скорость теплового движения
свободных электронов составляет величину ~105 м/с
Слайд 8
Однако в рамках этой теории возникли трудности. Из
теории следовало, что удельное сопротивление должно быть пропорционально корню
квадратному из температуры , между тем, согласно опыту, ρ ~ Т. Кроме того, теплоемкость металлов, согласно этой теории, должна быть значительно больше теплоемкости одноатомных кристаллов. В действительности теплоемкость металлов мало отличается от теплоемкости неметаллических кристаллов. Эти трудности были преодолены только в квантовой теории.
Слайд 9
Скорость упорядоченного движения электронов
в металле
Оценим скорость упорядоченного движения электронов в
металле,
считая, что на каждый атом металла приходится по
одному свободному электрону.
Пусть по проводнику сечением S=1 мм2 течет ток I=10 А
где n – концентрация электронов
Если масса вещества в единице объема – это плотность ρ, а
μ – молекулярный вес, то ρ/μ - это число молей в единице
объема. NА- число Авогадро –число атомов в одном моле.
Откуда и
Слайд 10
М.б. самостоятельно найти для меди и сравнить с
тепловой
Слайд 11
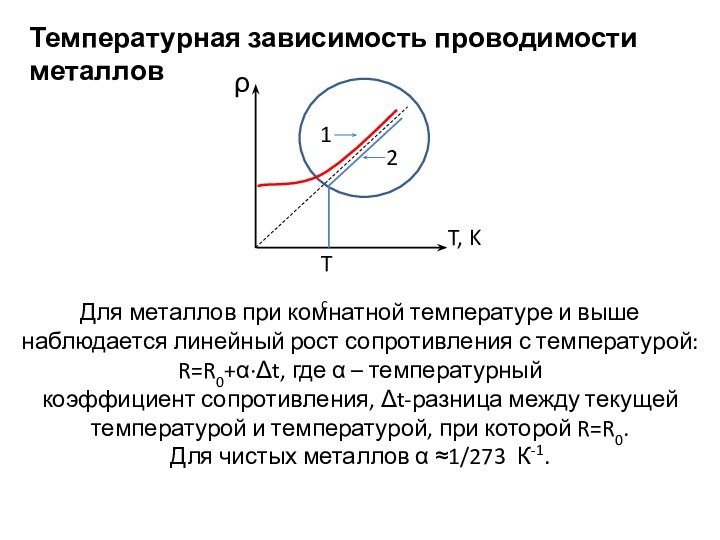
Температурная зависимость проводимости металлов
Для металлов при комнатной температуре
и выше наблюдается линейный рост сопротивления с температурой: R=R0+α·Δt,
где α – температурный
коэффициент сопротивления, Δt-разница между текущей температурой и температурой, при которой R=R0.
Для чистых металлов α ≈1/273 К-1.
1
2
T, K
Tc
ρ
Слайд 12
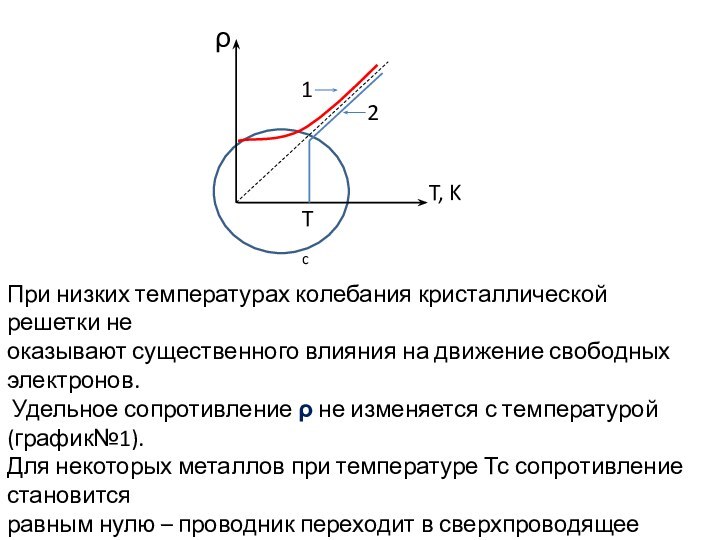
При низких температурах колебания кристаллической решетки не
оказывают
существенного влияния на движение свободных электронов.
Удельное сопротивление ρ
не изменяется с температурой (график№1).
Для некоторых металлов при температуре Тс сопротивление становится
равным нулю – проводник переходит в сверхпроводящее состояние
(график №2)
1
2
T, K
Tc
ρ
Слайд 14
Понятие о работе выхода
Работа выхода – это энергия,
которую необходимо затратить,
чтобы удалить электрон из металла в
вакуум на ∞
Слайд 15
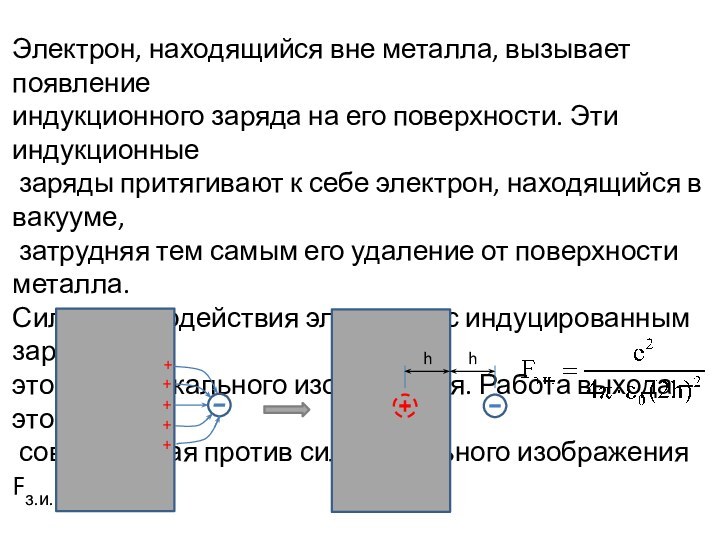
Электрон, находящийся вне металла, вызывает появление
индукционного заряда на
его поверхности. Эти индукционные
заряды притягивают к себе электрон,
находящийся в вакууме,
затрудняя тем самым его удаление от поверхности металла.
Сила взаимодействия электрона с индуцированным зарядом –
это сила зеркального изображения. Работа выхода – это работа,
совершаемая против сил зеркального изображения Fз.и.
+
+
+
+
+
h
h
Слайд 16
Интегрировать от поверхности металла (х=0) нельзя, т.к.
интеграл
расходится, работа равна бесконечности
Как быть ???
Концентрация свободных электронов
в металле ~1028 м-3 и
она не может измениться скачком до нуля на переходе металл-
вакуум – часть электронного облака «выпирает» наружу и на
границе металл-вакуум образуется двойной электрический слой
Слайд 17
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
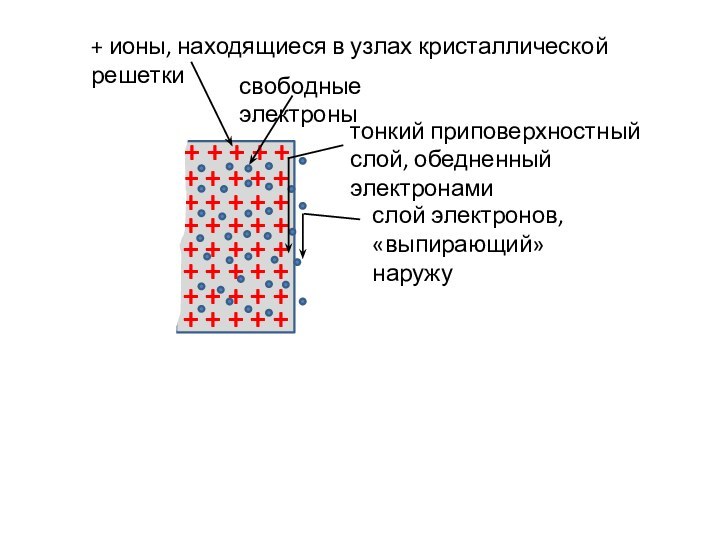
+ ионы, находящиеся в узлах кристаллической решетки
свободные электроны
тонкий
приповерхностный
слой, обедненный электронами
слой электронов,
«выпирающий» наружу
Слайд 18
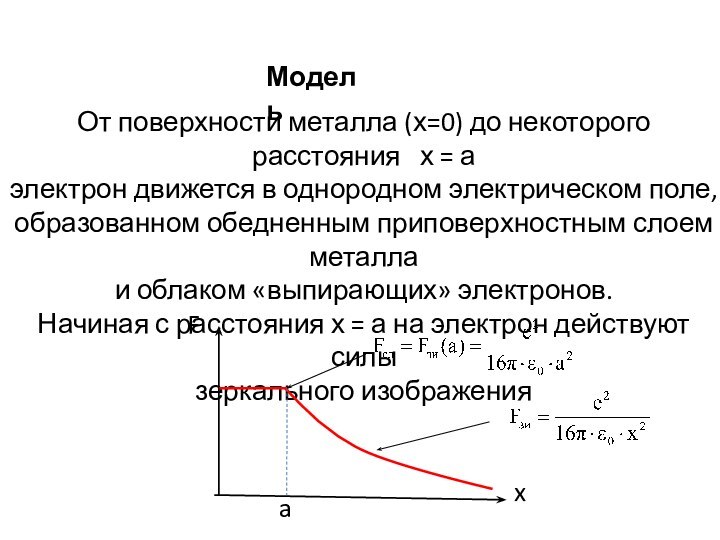
Модель
От поверхности металла (х=0) до некоторого расстояния
х = а
электрон движется в однородном электрическом поле,
образованном обедненным
приповерхностным слоем металла
и облаком «выпирающих» электронов.
Начиная с расстояния х = а на электрон действуют силы
зеркального изображения
F
x
a
Слайд 19
Тогда работа выхода складывается из работы по преодолению
двойного электрического слоя и работы против сил зеркального
изображения
Слайд 20
Контактная разность потенциалов
(КРП)
Слайд 21
Приведем в соприкосновение два различных металла.
В каждом из
металлов имеются свободные электроны и
поэтому возникает поток электронов из
одного металла в
другой и наоборот.
Вопрос: от чего зависит величина тока исходящего из
металла?
Очевидно: чем выше концентрация свободных носителей
тока, тем больше ток;
чем меньше работа выхода, тем больше ток;
Мет.1
Мет.2
Слайд 22
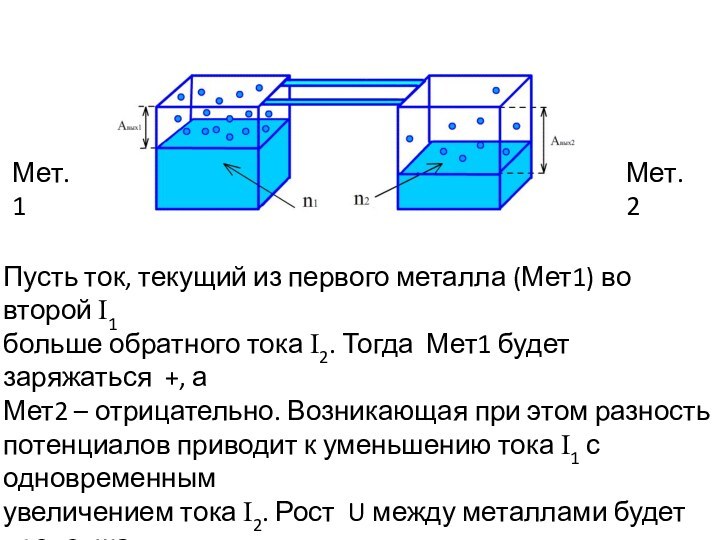
Мет.1
Мет.2
Пусть ток, текущий из первого металла (Мет1) во
второй I1
больше обратного тока I2. Тогда Мет1 будет
заряжаться +, а
Мет2 – отрицательно. Возникающая при этом разность
потенциалов приводит к уменьшению тока I1 с одновременным
увеличением тока I2. Рост U между металлами будет продолжа-
ться до тех пор, пока не произойдет выравнивание токов I1= I2 .
Возникающая при этом разность потенциалов носит название
КОНТАКТНОЙ РАЗНОСТИ ПОТЕНЦИАЛОВ - Uкрп
Слайд 23
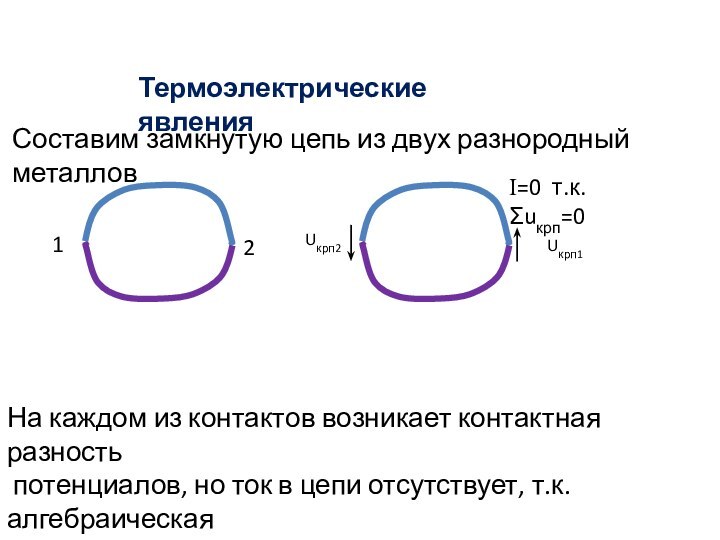
Термоэлектрические явления
Составим замкнутую цепь из двух разнородный металлов
1
2
Uкрп1
Uкрп2
I=0
т.к. Ʃuкрп=0
На каждом из контактов возникает контактная разность
потенциалов, но ток в цепи отсутствует, т.к. алгебраическая
сумма U крп равна нулю.
Слайд 24
Для того, чтобы в этой цепи возник электрический
ток
необходимо нарушить условия динамического равновесия
на одном
из контактов – изменить его температуру.
Тогда │U крп1│≠│U крп2│, I ≠ 0 , в цепи возникает термо ЭДС.
Т1
Т2
εтермо= α (Т2-Т1)
где α- коэффициент термоЭДС,
зависящий от природы соединяемых
материалов
Слайд 25
Практическое использование …………
термопара
mV
Tx
To
Один из спаев разнородных металлов находится
при известной температуре То. ( на рисунке это вода,
в которой плавает лед – 0оС). Второй спай помещается туда, где необходимо измерить температуру (Тх).
Предварительно для данной пары металлов производится градуировка милливольтметра
и по его показаниям определяется величина Тх
согласно соотношению: U= α (Т0-Тx)
Слайд 26
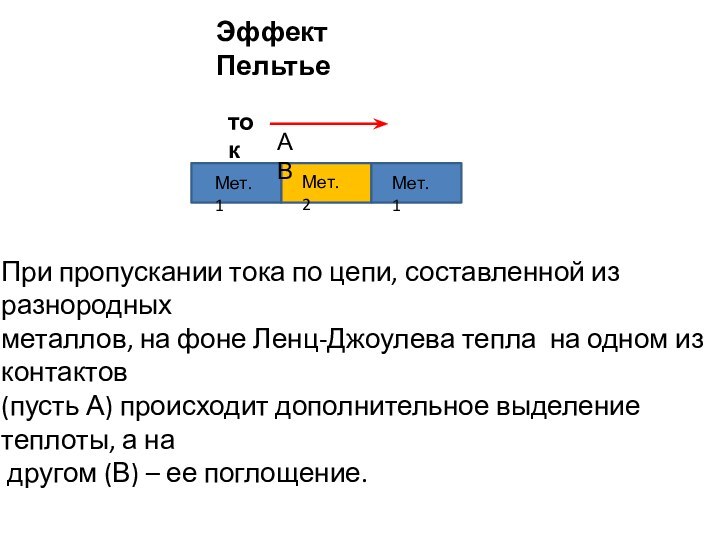
Эффект Пельтье
Мет.1
Мет.1
Мет.2
ток
А
В
При пропускании тока по цепи, составленной из разнородных
металлов, на
фоне Ленц-Джоулева тепла на одном из контактов
(пусть А) происходит дополнительное выделение теплоты, а на
другом (В) – ее поглощение.
Слайд 27
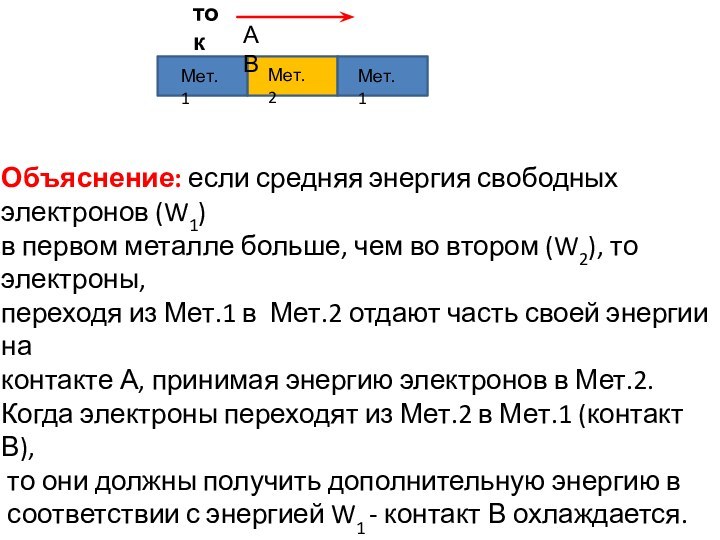
Объяснение: если средняя энергия свободных электронов (W1)
в первом
металле больше, чем во втором (W2), то электроны,
переходя из
Мет.1 в Мет.2 отдают часть своей энергии на
контакте А, принимая энергию электронов в Мет.2.
Когда электроны переходят из Мет.2 в Мет.1 (контакт В),
то они должны получить дополнительную энергию в
соответствии с энергией W1 - контакт В охлаждается.
Мет.1
Мет.1
Мет.2
ток
А В
Слайд 28
Дополнительное тепло, выделяющееся на одном из
контактов или
поглощаемое на другом, определяется
соотношением: ΔQ =
П· I·t, где П – коэффициент
Пельтье, величина которого зависит от природы
контактирующих материалов, I- сила тока, t- время
Для металлов этот эффект сравнительно невелик, однако
для полупроводниковых материалов он нашел практическое
применение – созданы полупроводниковые холодильники, а в последнее время полупроводниковые модули используются
и для охлаждения электронных элементов компьютеров
Слайд 29
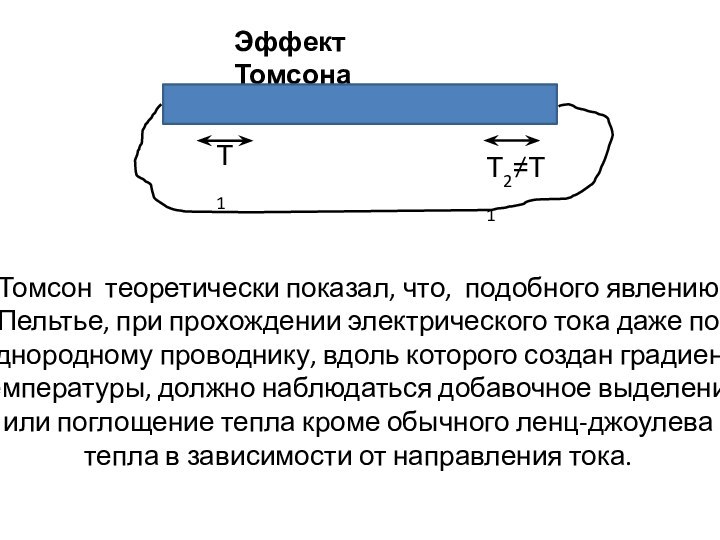
Эффект Томсона
Т1
Т2≠Т1
Томсон теоретически показал, что, подобного явлению
Пельтье, при
прохождении электрического тока даже по
однородному проводнику, вдоль которого создан
градиент
температуры, должно наблюдаться добавочное выделение
или поглощение тепла кроме обычного ленц-джоулева
тепла в зависимости от направления тока.
Слайд 30
Электрический ток в полупроводниках
Слайд 31
Как и в случае металлов, прохождение электрического тока
по
полупроводнику не связано с переносом вещества и
обусловлено движением
электронов.
Проводимость полупроводников существенно ниже, чем у
металлов, но в отличие от металлов она изменяется в широких
пределах в зависимости от наличия примесей и различного
рода внешних воздействий – нагрева или охлаждения,
облучения светом и микрочастицами
В настоящее время полупроводники- это фундамент микро-
и нано- электроники, бытовой электроаппаратуры
Слайд 32
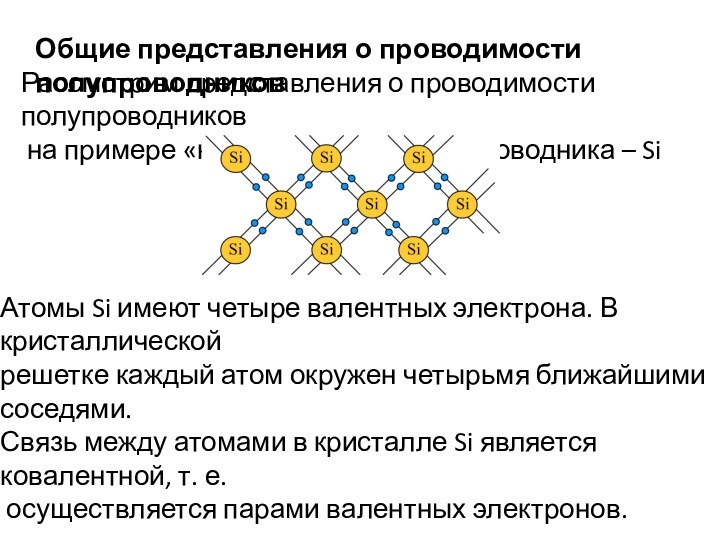
Общие представления о проводимости полупроводников
Рассмотрим представления о проводимости
полупроводников
на примере «классического» полупроводника – Si
Атомы Si имеют
четыре валентных электрона. В кристаллической
решетке каждый атом окружен четырьмя ближайшими соседями.
Связь между атомами в кристалле Si является ковалентной, т. е.
осуществляется парами валентных электронов.
Идеальный кристалл Si при температуре Т=0 К
является изолятором
Слайд 33
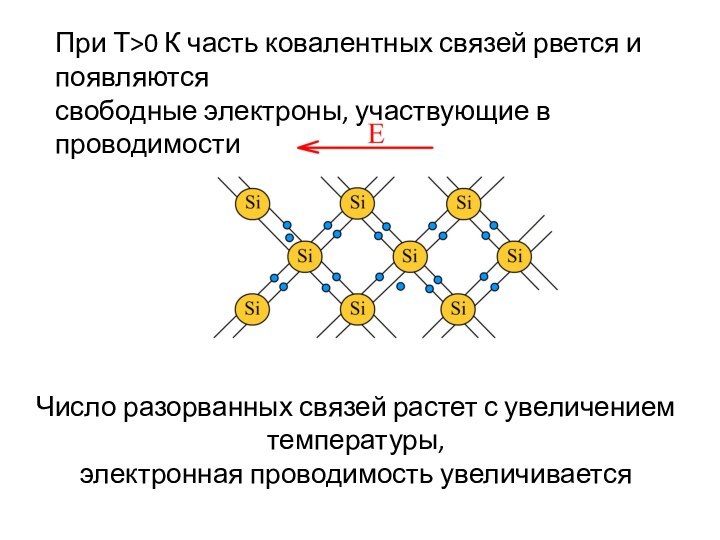
При Т>0 К часть ковалентных связей рвется и
появляются
свободные электроны, участвующие в проводимости
Число разорванных связей
растет с увеличением температуры,
электронная проводимость увеличивается
Слайд 34
Обрыв связей и появление свободных электронов приводит еще
к одному эффекту, увеличивающему проводимость: электроны
соседних атомов перескакивают
на освобожденное место и
возникает так называемая дырочная проводимость
Пустое место (вакансия), заряженная +, перемещается по полю,
создавая эффект движения + заряда – дырочная проводимость
Слайд 35
Зонная модель полупроводников
При Т=0 К валентная зона
заполнена
полностью,
зона проводимости - пуста
Электроны, полностью заполняющие зону, не
могут участвовать в электрическом токе – под действием электрического поля на длине свободного пробега они должны двигаться с ускорением, т. е. переходить на более высокий энергетический уровень. Однако все уровни уже заняты.
При Т=0 К полупроводник является изолятором
Слайд 36
При Т>0 К часть электронов из валентной зоны,
преодолев запрещенную зону, переходит в зону проводимости.
Электроны в зоне
проводимости участвуют в
электрическом токе- электронная проводимость
(полупроводник n типа)
Электроны в валентной зоне также участвуют в
электрическом токе т.к. появились свободные
энергетические состояния- дырочная проводимость (полупроводник р типа)
Интенсивность перехода электронов из валентной зоны в зону
проводимости растет с увеличением температуры
Проводимость полупроводников растет с температурой
Слайд 37
Влияние примесей на проводимость полупроводников
Если в кристаллическую решетку
Si –
элемента 4-ой группы внедрить атомы из
5-ой группы, имеющих
лишний электрон,
то в зонной модели появится энергети-
ческий уровень в запрещенной зоне
вблизи дна зоны проводимости,
заполненный электронами.
При Т=0 К проводимость отсутствует.
При Т>0 К электроны переходят в зону проводимости – возникает электронная проводимость
При дальнейшем увеличении температуры начинается интенсивный
переброс электронов из валентной зоны в зону проводимости –
это уже собственная проводимость
Слайд 38
Если в кристаллическую решетку Si –
элемента 4-ой группы,
внедрить атомы
из 3-ей группы, имеющих электронов на
один
меньше, то в зонной модели
появится энергетический уровень в
запрещенной зоне вблизи вершины
валентной зоны не заполненный
электронами.
При Т=0 К проводимость отсутствует.
При Т>0 К электроны переходят из валентной зоны на акцепторные уровни, появляются свободные состояния в валентной зоне – возникает дырочная проводимость
При дальнейшем увеличении температуры начинается интенсивный
переброс электронов из валентной зоны в зону проводимости –
это уже собственная проводимость
Слайд 39
Влияние света на проводимость полупроводников
Если ширина запрещенной зоны
ΔЕ меньше
энергии кванта света hu, то
возникает так
называемый внутренний фотоэффект –
переброс электронов из валентной зоны в
зону проводимости
Появление электронов в зоне проводимости и свободных мест в валентной зоне приводит к увеличению проводимости
полупроводника.
Слайд 40
Контактные явления
Как уже говорилось ранее контактные явления
– эффекты
Зеебека, Пельтье, Томсона в полупроводниках проявляются
существенно более
ярко по сравнению с металлами, что и
позволило использовать эти материалы для создания
изделий в промышленном масштабе
Современный автомобильный полупроводниковый
холодильник, работа которого основана на эффекте
Пельтье
Старинный термоэлектрический генератор, работа
которого основана на эффекте Зеебека.
Он устанавливался на керосиновые лампы и
использовался в 60-ые годы для питания
радиоприемников
Слайд 41
р-n переход
Первооснова полупроводниковой электроники – это р-n пере-
ход, образующийся на контакте полупроводников р и n типов
Проводимость
полупроводников n типа в основном
осуществляется за счет электронов - основные носители,
дырки являются неосновными носителями
Проводимость полупроводников р типа в основном
осуществляется за счет дырок- основные носители,
электроны являются неосновными носителями
Слайд 42
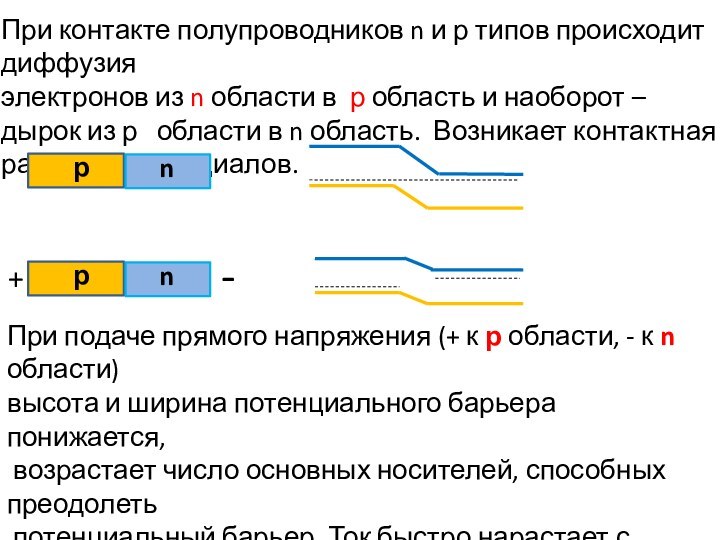
При контакте полупроводников n и р типов происходит
диффузия
электронов из n области в р область и наоборот
– дырок из р области в n область. Возникает контактная разность потенциалов.
р
n
р
n
+
-
При подаче прямого напряжения (+ к р области, - к n области)
высота и ширина потенциального барьера понижается,
возрастает число основных носителей, способных преодолеть
потенциальный барьер. Ток быстро нарастает с увеличением
приложенного напряжения.
Слайд 43
р
n
р
n
+
-
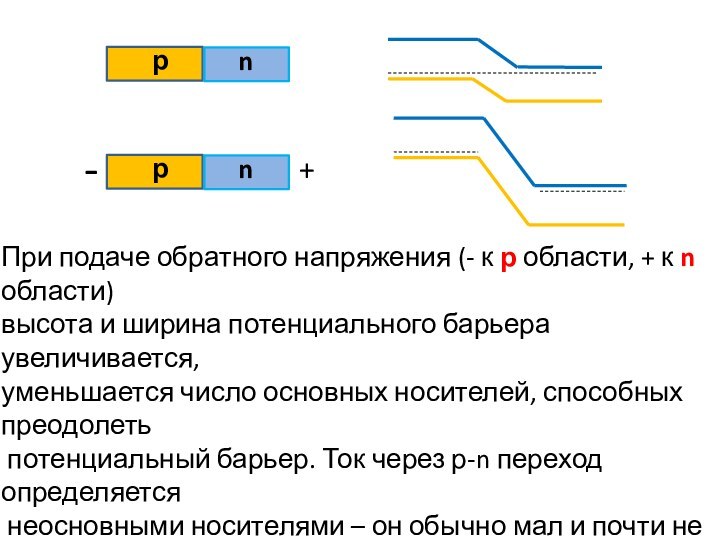
При подаче обратного напряжения (- к р области,
+ к n области)
высота и ширина потенциального барьера увеличивается,
уменьшается
число основных носителей, способных преодолеть
потенциальный барьер. Ток через р-n переход определяется
неосновными носителями – он обычно мал и почти не
зависит от напряжения.
При изменении знака U значение тока через переход может
изменяться в 105 — 106 раз. Благодаря этому p-n-переход
используется для выпрямления переменных токов