Презентация на тему Фазовые портреты. Особые точки

второго порядка в виде двух уравнений первого порядка:
или
Для исключения

Разделим переменные:

Проинтегрировав уравнение, получим

или

где С – постоянная интегрирования (начальные условия).

Последнее уравнение можно записать как

y

z

Это уравнение эллипса.

Задаваясь различными начальными условиями, получим фазовый портрет системы.

Полученное уравнение есть уравнение фазовых траекторий рассматриваемой системы.

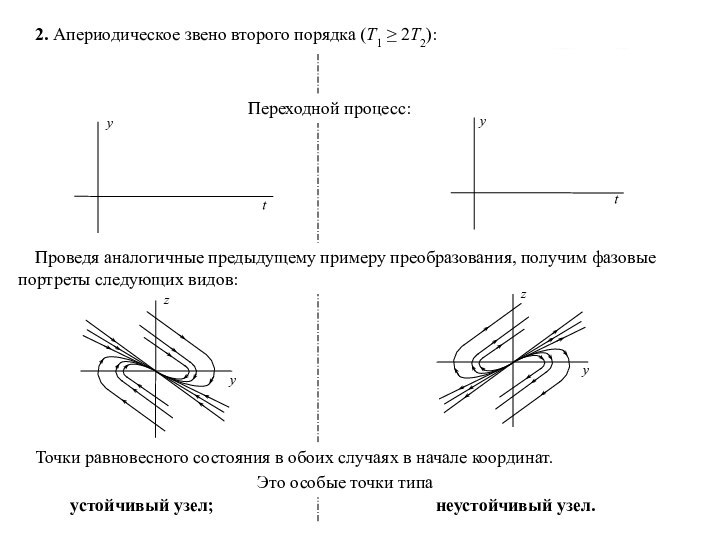
Здесь одна точка равновесного состояния – начало координат.

Это особая точка типа центр.

?

(вариант)
y
y
z
y
t
Переходной процесс:
Проведя аналогичные предыдущему примеру преобразования, получим фазовые портреты

Точки равновесного состояния в обоих случаях в начале координат.

Это особые точки типа

устойчивый узел;

неустойчивый узел.

z

t

y

звено.
Фазовые портреты
Равновесное состояние в начале координат.
Это особые точки типа
устойчивый

неустойчивый фокус

y

z

Если переходной процесс следующего характера,

фазовый портрет имеет вид

Здесь особая точка типа седло (в начале координат).

t

y

Например, точки типа центр (0) и седло (а).
ОСОБЕННОСТИ ФАЗОВЫХ

а

0

z

y

На фазовых портретах нелинейных систем могут быть особые отрезки равновесных состояний (выделен).

y

z

y

z

Линия, разделяющая области с разными типами фазовых траекторий, называется сепаратриссой (выделена).

Важными особыми кривыми являются предельные циклы – замкнутые кривые, соответствующие периодическим процессам.

y

z

и снаружи расходятся от предельного цикла, то это неустойчивый предельный цикл.

Устойчивый предельный цикл

Если фазовые траектории внутри

Если фазовые траектории сходятся к предельному циклу – это устойчивый предельный цикл.

Суть устойчивого предельного цикла – автоколебания.

Автоколебания – свободные пери-одические колебания без внешних периодических воздействий.