- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрические построения
Содержание
- 2. Деление отрезков и прямых на равные части
- 3. Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.
- 4. Из концов отрезка АВ циркулем проводят две
- 5. Точки m и n соединяют прямой, которая
- 7. ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ
- 8. Некоторые детали машин и приборов имеют элементы,
- 10. Деление окружности на три, шесть и двенадцать равных частей.
- 11. Для нахождения точек, делящих окружность радиуса R
- 13. При делении окружности циркулем на шесть равных
- 15. СОПРЯЖЕНИЕ ДВУХ СТОРОН УГЛА ДУГОЙ ЗАДАННОГО РАДИУСА
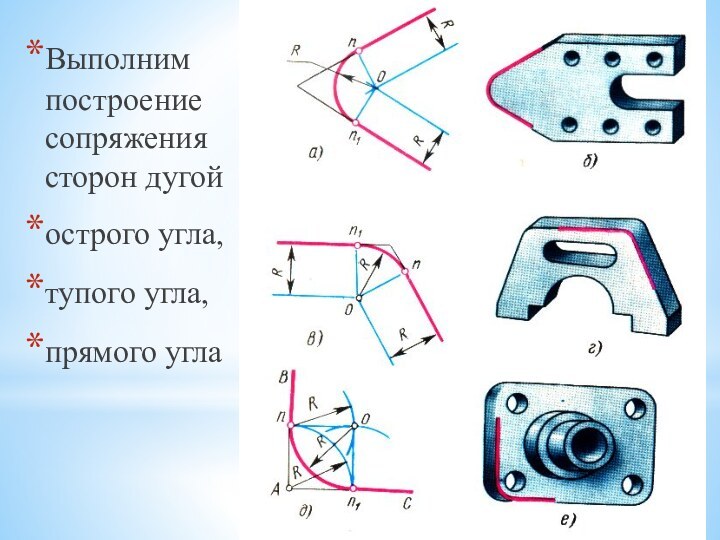
- 16. Выполним построение сопряжения сторон дугой острого угла, тупого угла, прямого угла
- 17. Сопряжение двух сторон угла (острого или тупого)
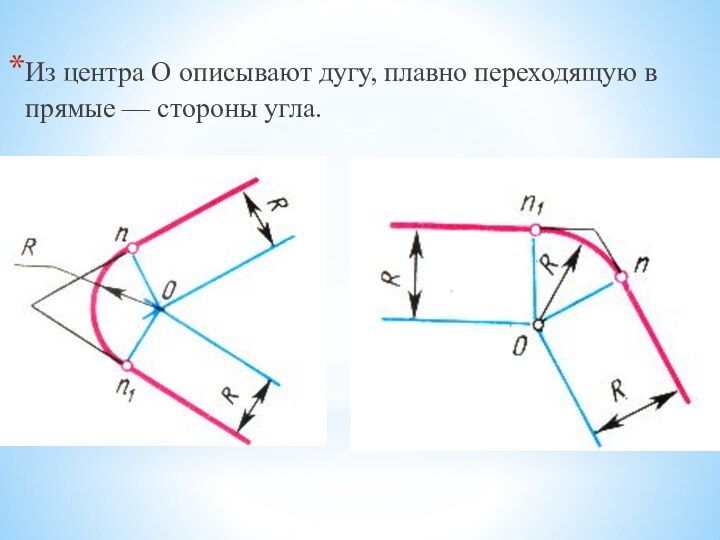
- 18. Из центра О описывают дугу, плавно переходящую в прямые — стороны угла.
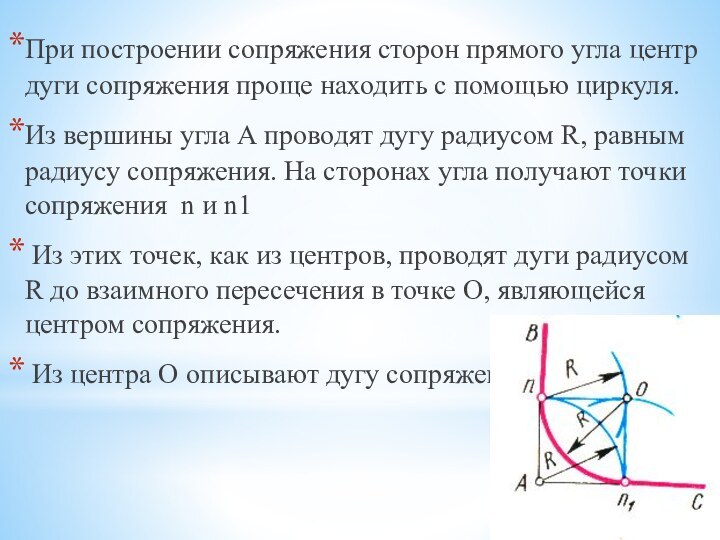
- 19. При построении сопряжения сторон прямого угла центр
- 20. Скачать презентацию
- 21. Похожие презентации
Деление отрезков и прямых на равные части











Слайд 3 Деление отрезка прямой на две и четыре равные
части выполняется в следующей последовательности.
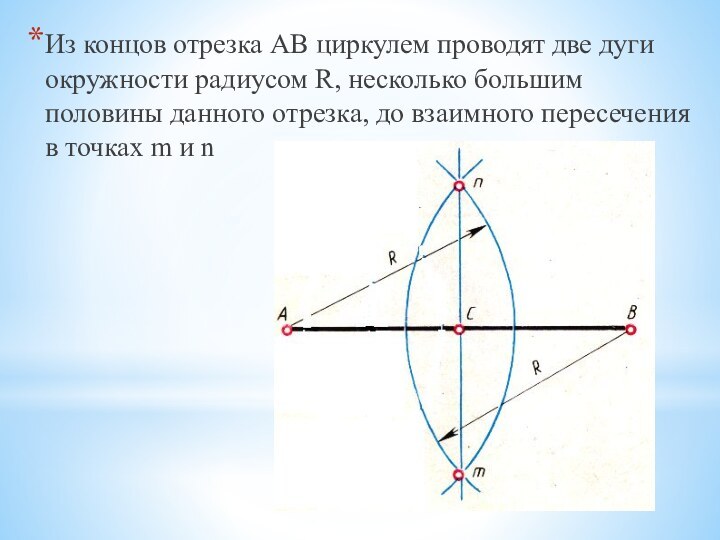
Слайд 4 Из концов отрезка АВ циркулем проводят две дуги
окружности радиусом R, несколько большим половины данного отрезка, до
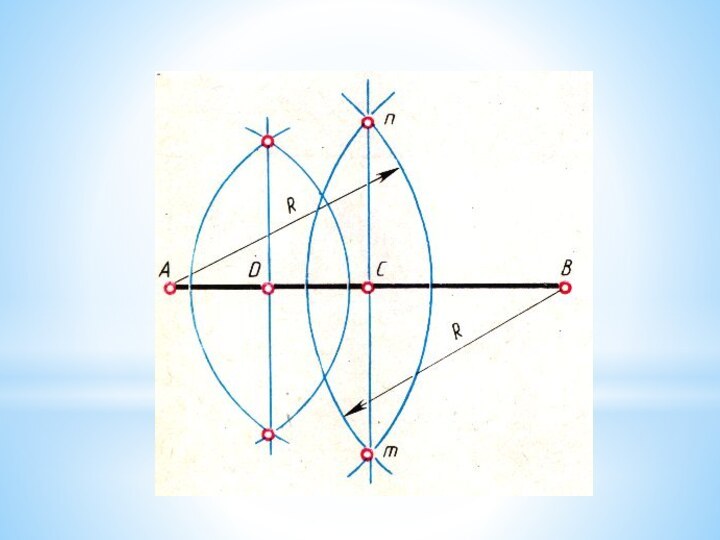
взаимного пересечения в точках m и nСлайд 5 Точки m и n соединяют прямой, которая пересекает
отрезок АВ в точке С.
Точка С делит отрезок
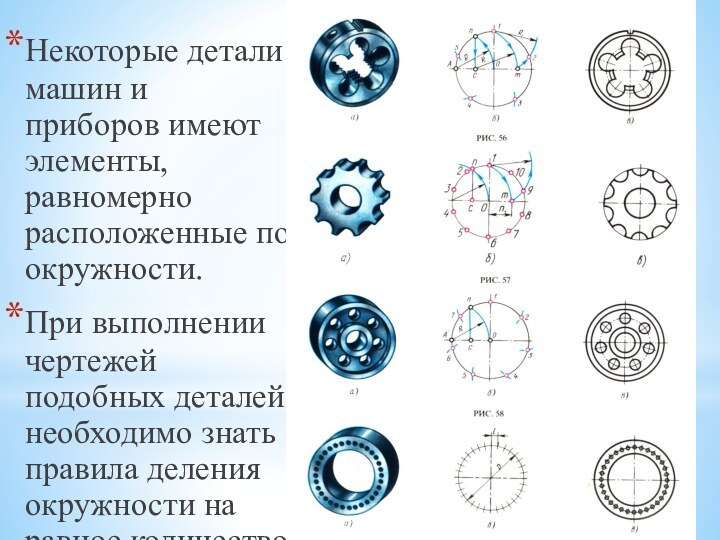
А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок А В на четыре равные части.Слайд 8 Некоторые детали машин и приборов имеют элементы, равномерно
расположенные по окружности.
При выполнении чертежей подобных деталей необходимо знать
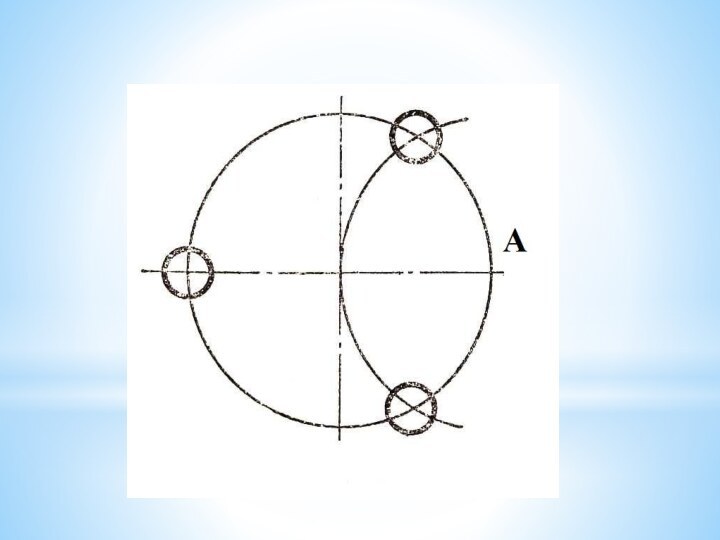
правила деления окружности на равное количество частей.Слайд 11 Для нахождения точек, делящих окружность радиуса R на
три равные части, достаточно из любой точки окружности, например
точки А, провести дугу радиусом R.Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки А, с окружностью
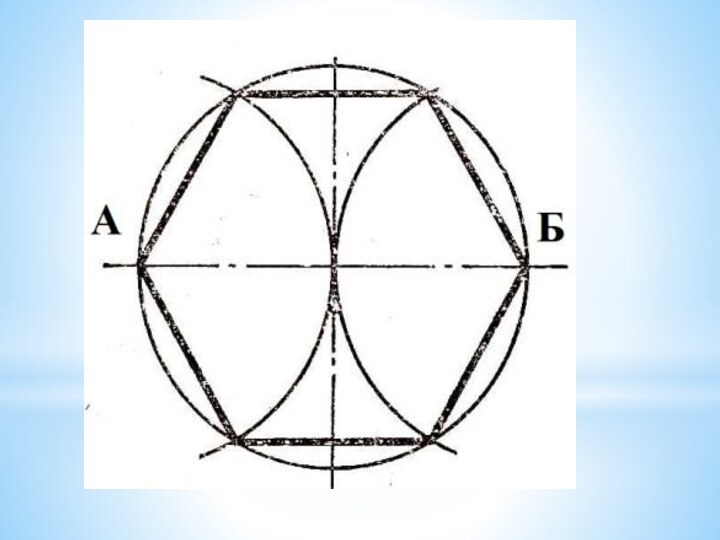
Слайд 13 При делении окружности циркулем на шесть равных частей
выполняется то же построение, что и при делении на
три, но дугу описывают не один, а два раза, из точек А и Б радиусом R, равным радиусу окружности.Слайд 17 Сопряжение двух сторон угла (острого или тупого) дугой
заданного радиуса R выполняют следующим образом
Параллельно сторонам угла
на расстоянии, равном радиусу дуга R, проводят две вспомогательные прямые линии. Точка пересечения этих прямых (точка О) будет центром дуги радиуса R, т. е. центром сопряжения.
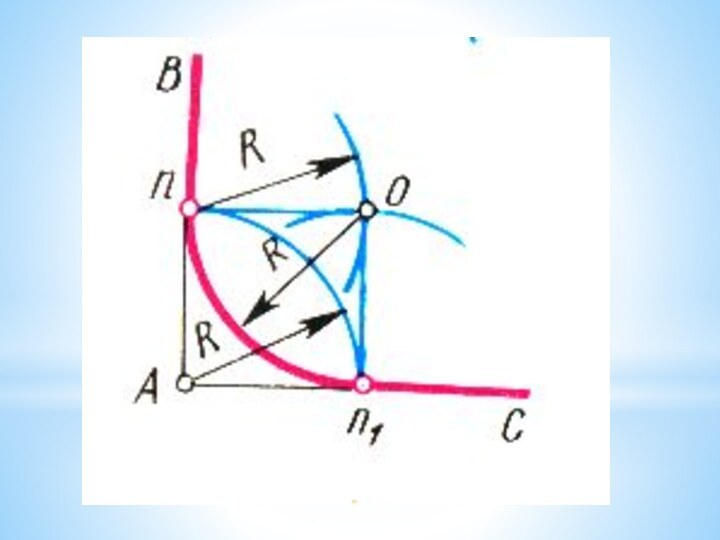
Слайд 19 При построении сопряжения сторон прямого угла центр дуги
сопряжения проще находить с помощью циркуля.
Из вершины угла
А проводят дугу радиусом R, равным радиусу сопряжения. На сторонах угла получают точки сопряжения n и n1Из этих точек, как из центров, проводят дуги радиусом R до взаимного пересечения в точке О, являющейся центром сопряжения.
Из центра О описывают дугу сопряжения.





























