- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Кодування інформації
Содержание
- 2. Чарльз Беббідж (1791-1871), англійський математик і інженер,
- 3. Леді-програміст Августа Ада Лавлейс Ада Лавлейс
- 4. Вільгельм Готфрід Лейбніц (1646-1716)Починаючи зі студентських
- 5. Значимість двійкової системи числення для кодування інформаціїВ
- 6. Двійкове кодування інформації
- 7. Чому двійкове кодування? З точки зору технічної реалізації
- 8. Система числения Для запису інформації про кількість
- 9. Двійкова система числення
- 10. Алфавіт десятковій, двійковій, вісімковій і шістнадцятковій систем числення
- 11. Відповідність десятковій, двійковій, вісімковій і шістнадцятковій систем
- 12. Переклад числа 19ЗАПИШЕМО!10 22 101919
- 13. Числа в комп'ютері зберігаються та обробляються в
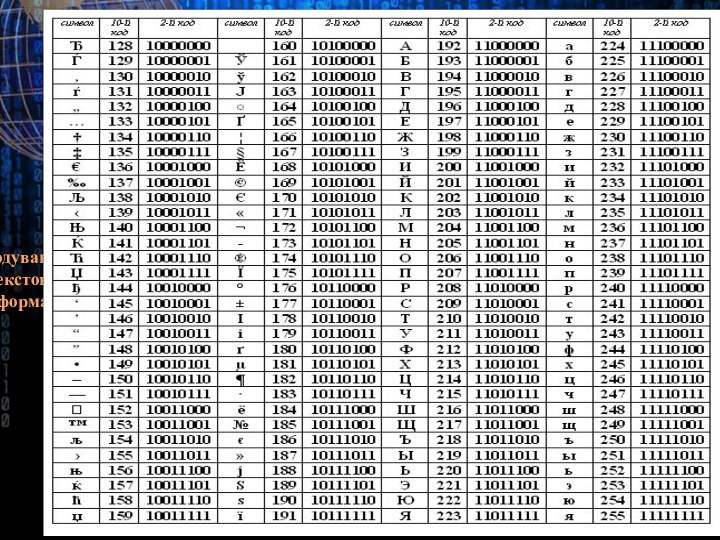
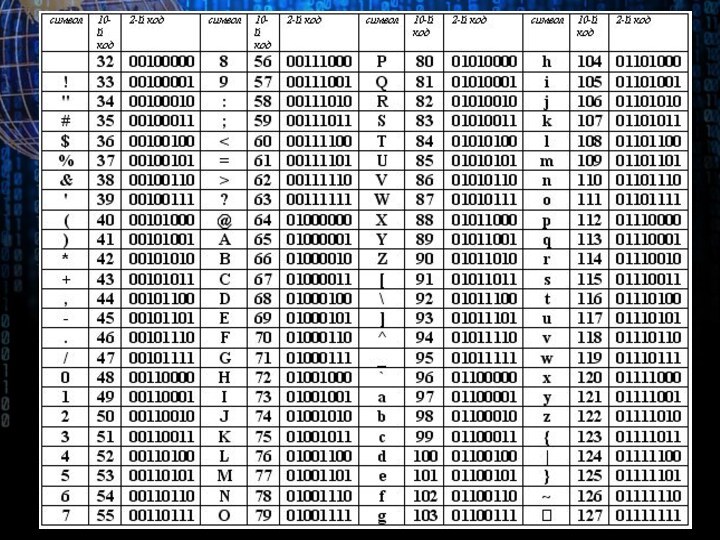
- 14. Кодування текстової інформації
- 16. ?Яку кількість комп'ютерів ви бачите? Відповідь дайте у двійковій, вісімковій і десятковій системах числення
- 17. Скачать презентацию
- 18. Похожие презентации
Чарльз Беббідж (1791-1871), англійський математик і інженер, розробив принципи, на основі яких конструюються всі сучасні комп'ютери.













Слайд 2
Чарльз Беббідж
(1791-1871),
англійський математик і інженер,
розробив принципи,
на основі яких
конструюються
всі
сучасні комп'ютери.
Слайд 3
Леді-програміст
Августа Ада Лавлейс
Ада Лавлейс запропонувала Чарльзу
Бэббиджу застосувати двійкову систему числення. Вона написала кілька програм для аналітичної машини, розробила
теорію програмування.
Слайд 4
Вільгельм Готфрід Лейбніц
(1646-1716)
Починаючи зі студентських
років і до
кінця життя великий європеєць, німецький учений Готфрід Вільгельм Лейбніц
займався дослідженням властивостей двійкової системи числення, що стала надалі основною при створенні комп'ютерів.Зображення медали В. Лейбніца
Слайд 5
Значимість двійкової системи числення для кодування інформації
В ЕОМ
використовують двійкову систему, тому що вона має ряд переваг перед
іншими системами:для її реалізації потрібні технічні елементи з двома можливими станами (є струм, немає струму; увімкнено, вимкнено і т.д.; одним із станів ставиться у відповідність 1, інакше - 0), а не десять, як у десятковій системі;
подання інформації за допомогою лише двох станів надійно і помехоустойчиво; спрощується виконання арифметичних дій;
можливість використання апарату булевої алгебри для виконання логічних перетворень інформації.
Слайд 6
Двійкове кодування інформації
Вся
інформація, яку обробляє комп'ютер повинна бути представлена двійковим кодом
за допомогою двох цифр: 0 та 1. Ці два символи прийнято називати двійковими цифрами або бітами. З допомогою двох цифр 0 і 1 можна закодувати будь-яке повідомлення. Це стало причиною того, що в комп'ютері обов'язково повинно бути організовано два важливих процеси: кодування і декодування.Кодування - перетворення вхідної інформації у форму, яка сприймається комп'ютером, тобто двійковий код.
Декодування - перетворення даних з двійкового коду у форму, зрозумілу людині.
Слайд 7
Чому двійкове кодування?
З точки зору технічної реалізації використання
двійкової системи числення для кодування інформації виявилося набагато простішим,
ніж застосування інших способів. Дійсно, зручно кодувати інформацію в вигляді послідовності нулів та одиниць, якщо уявити ці значення як два можливих стійких стани електронного елемента:0 – відсутність електричного сигналу;
1 – наявність електричного сигналу.
Способи кодування і декодування інформації в комп'ютері, в першу чергу, залежить від виду інформації, а саме, що має кодуватися: числа, текст, графічні зображення або звук.
Слайд 8
Система числения
Для запису інформації про кількість об'єктів
використовуються числа. Числа записуються за допомогою набору спеціальних символів.
Система
числення - спосіб запису чисел за допомогою набору спеціальних знаків, які називаються цифрами.
Слайд 11
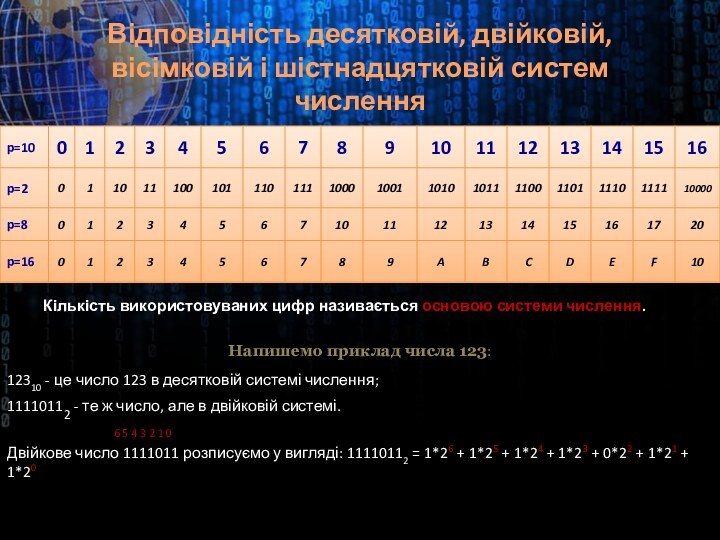
Відповідність десятковій, двійковій, вісімковій і шістнадцятковій систем числення
Кількість
використовуваних цифр називається основою системи числення.
Напишемо приклад числа 123:
12310
- це число 123 в десятковій системі числення;
11110112 - те ж число, але в двійковій системі.Двійкове число 1111011 розписуємо у вигляді: 11110112 = 1*26 + 1*25 + 1*24 + 1*23 + 0*22 + 1*21 + 1*20
6 5 4 3 2 1 0
Слайд 12
Переклад числа 19
ЗАПИШЕМО!
10 2
2 10
19
19 =100112
100112
4
3 2 1 0
разряды
= 1·24 + 0·23 + 0·22
+ 1·21 + 1·20= 16 + 2 + 1 = 19
1
1
0
0
1





























