- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комбинаторика
Содержание
- 2. Что это? Комбинаторика – раздел науки,
- 3. «Забавные и приятные задачи, которые решаются в
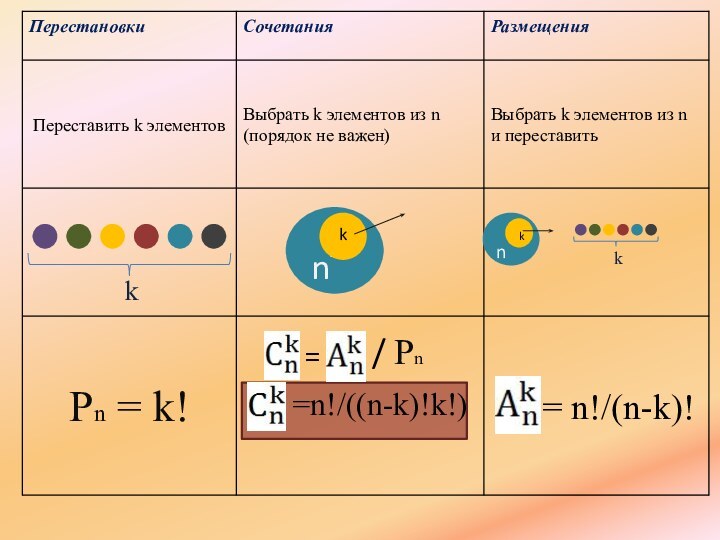
- 4. Перестановки Перестановка – конечное множество, в котором
- 5. Возьмем слово из n различных букв и
- 6. Пример задач на перестановки 1. Сколько различных
- 7. Решите сами:Сколько анаграмм можно получить из слова
- 8. Размещения Без повторений:Сколько k-буквенных слов с
- 9. Размещения с повторениямиНа 1 место ставим любую
- 10. 1) Сколько существует различных автобусных билетиков из
- 11. Снова представим, что выписываем слова с разными
- 12. В вагоне есть 10 свободных мест. В
- 13. СочетанияОпределение: Подмножества, составленные из n элементов данного
- 14. = / Pn
- 15. Примеры решения задачСколькими способами можно выбрать трех
- 16. 1. Сколько попыток было бы достаточно, чтобы
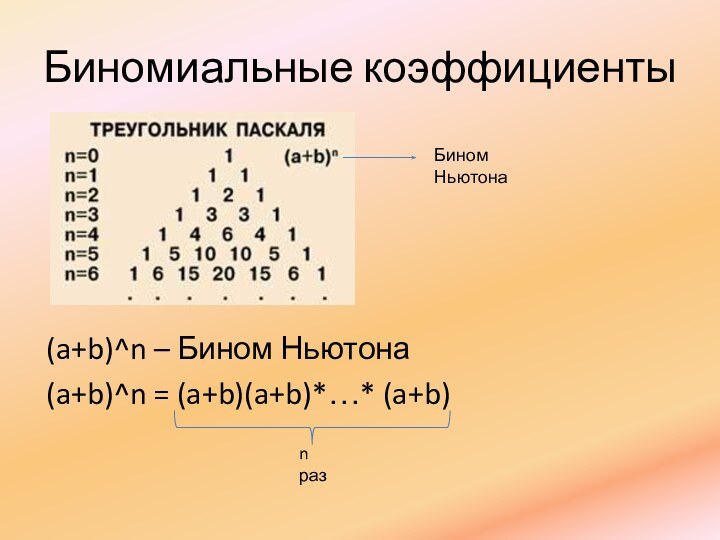
- 17. Биномиальные коэффициенты(a+b)^n – Бином Ньютона(a+b)^n = (a+b)(a+b)*…* (a+b) Бином Ньютона
- 18. Скачать презентацию
- 19. Похожие презентации
Что это? Комбинаторика – раздел науки, в котором изучаются комбинаторные задачи. Комбинаторика имеет дело с перебором вариантов и подсчетом их числа.
















Слайд 2
Что это?
Комбинаторика – раздел науки, в
котором изучаются комбинаторные задачи.
вариантов и подсчетом их числа.Слайд 3 «Забавные и приятные задачи, которые решаются в числах»
1612г.
Баше де Меризиак – французский математик, философ
и поэт.
Слайд 4
Перестановки
Перестановка – конечное множество, в котором установлен
порядок его элементов.
Например: ПУХ, УПХ, ХУП, ПХУ, УХП, ХПУ
Получили
6 различных перестановок из 3 букв.Слайд 5 Возьмем слово из n различных букв и составим
все его анаграммы:
На 1 место ставим любую из
n буквНа 2 место – любую из n-1 оставшихся
На 3 место – любую из n-2 оставшихся ит.д.
Кол-во перестановок Pn = n(n-1)(n-2)*…*2*1
Pn = 1*2*…*(n-2)(n-1)n = n! (факториал)
Pn = n!
Слайд 6
Пример задач на перестановки
1. Сколько различных трехцветных
флагов с тремя горизонтальными полосами можно получить, используя зеленый,
пурпурный и желтый цвета?2.Имеется 10 различных книг, среди которых есть трехтомник. Сколькими способами можно расставить эти книги на полке, так что книги трехтомника стоят вместе, но в любом порядке?
Слайд 7
Решите сами:
Сколько анаграмм можно получить из слова «бремя»?
Сколькими способами можно сесть на рельсы 7
людям? 3) Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы они не били друг друга?
4) Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
8! = 40320
20!/20 = 19!
5! = 120
7! = 5040
Слайд 8
Размещения
Без повторений:
Сколько k-буквенных слов с разными
буквами можно составить из алфавита, содержащего n букв?
С повторениями:
Сколько
k-буквенных слов можно составить из алфавита, содержащего n букв?
Слайд 9
Размещения с повторениями
На 1 место ставим любую из
n букв
На 2 место ставим любую из n букв
(и так k раз).Получим: n*n*n*…*n =
k раз
=
Слайд 10 1) Сколько существует различных автобусных билетиков из 6
цифр?
2) Сколько существует различных автобусных билетиков из 6
цифр, так чтобы на 4 месте стояло нечетное число, а на 2 месте либо 3, либо 5, либо 7? Размещения с повторениями проще рассматривать как произведение количества вариантов на каждом месте.
Размещения с повторениями
Слайд 11
Снова представим, что выписываем слова с разными буквами.
На
первое место ставим любую из n букв.
На 2 место
– любую из n-1 оставшихся ит.д.K) На k место ставим одну из n-(k-1) оставшихся.
Получим: = n(n-1)(n-2)*…* (n-k+1)
Умножим на (n-k)!/(n-k)!
n(n-1)(n-2)*…* (n-k+1)*(n-k)!/(n-k)! = n!/(n-k)!
= n!/(n-k)!
Размещения без повторений
Слайд 12 В вагоне есть 10 свободных мест. В вагон
вошли 6 пассажиров. Сколькими способами они смогут разместиться в
этом вагоне на свободных местах?Сколькими способами могут быть присуждены первая вторая и третья премии трем лицам из 10 соревнующихся?
Номер машины состоит из 3-х букв 26-буквенного алфавита и четырех цифр. Сколько существует различных номеров автомашин?(возможен номер ааа0000) 26^3 *10^4
Задачи:
Слайд 13
Сочетания
Определение: Подмножества, составленные из n элементов данного множества
и содержащие k элементов в каждом подмножестве, называют сочетанием
из n элементов по k.По сути - число способов выбрать некоторое количество элементов из данного множества.
Пишется –
Читается – «С из n по k»
Слайд 15
Примеры решения задач
Сколькими способами можно выбрать трех дежурных
из нашего класса (32 человека)?
В вазе стоят 10
красных и 5 белых роз. Выбирают две красные и одну белую розу. Сколько различных букетов можно составить?Слайд 16 1. Сколько попыток было бы достаточно, чтобы взломать
кодовый замок от входной двери (раньше везде такие стояли,
пароль состоит из 3 цифр, которые нужно нажать одновременно)?2. Каким числом способов можно выбрать из 30 человек команду из 6 человек и среди них одного капитана?
3. Сколько человек участвовало в шахматном турнире, если известно, что каждый участник сыграл с каждым из остальных по одной партии и всего было сыграно 136 партий?
4. Замок в автоматической камере хранения открывается лишь после того, как набирается определенный набор из четырех цифр. Пассажир забыл набранный номер, но помнил, что в нем все цифры были разные и шли они в порядке возрастания. Какое наибольшее количество комбинаций цифр ему придется перебрать, чтобы открыть замок?
Задачи:
17





























