Слайд 2
Комбинаторика – это раздел дискретной математики, в котором
изучаются вопросы о том, сколько различных комбинаций можно составить
из заданных элементов (объектах) с учетом тех или иных условий.
Комбинаторика возникла в XVII веке. Первоначально комбинаторные задачи касались в основном азартных игр.
Комбинаторика
Слайд 3
Сочетания
Перестановки
С повторением
Без повторения
Размещения
С повторением
Без повторения
Комбинаторные конфигурации
Слайд 4
Опр. Перестановкой без повторений из n элементов называется
всякий кортеж длины n из n разных заданных элементов.
Рn
= n!
Задача №1.
Сколькими способами 4 человека могут разместиться на четырехместной скамейке?
Решение:
Р4 = 1* 2* 3* 4=24
Ответ: 24.
Слайд 5
Задача №2.
Сколько различных четырехзначных чисел, в которых цифры
не повторяются, можно составить из чисел 0,2, 4.6?
Решение: из
цифр 0,2.4.6 можно составить Р4 перестановок. Из этого числа нужно исключить те перестановки, которые начинаются с 0.
Число таких перестановок Р3. Значит искомое число четырехзначных чисел, которые можно составить из цифр 0,2,4,6 равно:
Р4 – Р3= 4!-3!= 1*2*3*4-1*2*3=24-6=18
Ответ: 18.
Слайд 6
Задача №3.
Имеются 9 различных книг, четыре из которых
учебники.
Сколькими способами можно расставить книги на полке так, чтобы
все учебники стояли рядом?
Решение: сначала будем рассматривать учебники как одну книгу. Тогда на полке надо расставить не 9, а 6 книг. Это можно сделать Р6 способами.
И в каждой из полученных комбинаций можно выполнить Р4 перестановок учебников. Значит, искомое число способов расположения книг равно произведению: Р6*Р4= 1*2*3*4*5*6*1*2*3*4 =17280
Ответ: 17280
Слайд 14
Обратимся теперь к истории появления
графов. Впервые в рассмотрение их ввел великий математик Леонард
Эйлер. Это был один из крупнейших математиков XVIII . Он родился в швейцарском городе Базеле, где в 15 лет закончил университет, а в 17 лет получил степень магистра. Во время обучения в университете Эйлер брал уроки у одного из самых известных математиков того времени Иоганна Бернулли. Нет такой области математики, где Эйлер не сказал своего слова. Работал он сутками напролет в любой обстановке, опубликовал примерно 850 работ. Он легко обнаруживал новые задачи и методы их решения.
Теория графов
Слайд 15
Графом называется конечное множество точек, некоторые из которых
соединены линиями.
Точки называются вершинами графа, а соединяющие линии –
рёбрами.
Количество рёбер, выходящих из вершины графа, называется степенью вершины.
Предложение 1.
Степени вершин полного графа одинаковы, и каждая из них на 1 меньше числа вершин этого графа.
Предложение 2.
Сумма степеней вершин графа число четное, равное удвоенному числу ребер графа.
Эта закономерность справедлива не только для полного, но и для любого графа.
Число нечетных вершин любого графа четно.
Эйлеров путь - путь в графе, проходящий через каждое ребро ровно один раз.
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым (уникурсальным).
Предложение 3.
Если все вершины графа четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.
Слайд 17
Предложение 4.
Граф, имеющий всего две нечетные вершины, можно
начертить, не отрывая карандаш от бумаги, при этом движение
нужно начать с одной из этих нечетных вершин и закончить во второй из них.
Предложение 5.
Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком».
Слайд 18
Задача 1. Дан кусок проволоки длиной 120 см.
Можно ли, не ломая проволоки, изготовить каркас куба 10
см?
Решение. Куб имеет 12 ребер, сумма длин которых равна 120 см. Если бы была возможность из проволоки длиной 120 см, не ломая ее изготовить каркас этого куба, то это означало бы, что граф состоящий из вершин и ребер куба, является уникурсальным. Но так как этот граф имеет 8 вершин третьей степени, то по теореме, приведенной выше, для его изображения необходимо 4 росчерка. Итак, ответ к задаче – отрицательный. Заметим, что для изготовления куба с ребром 10 см необходимо либо проволоку 120 см разрезать 3 раза, либо использовать кусок проволоки длиной 150 см и по каким-то трем ребрам проложить ее дважды.
(Исп. предложение 6)
Слайд 19
Задача 2.
Говорят, что Магомет вместо подписи (он был
неграмотен) описывал одним росчерком состоящий из двух рогов луны
знак, представленный на рисунке. Возможно ли это? Нарисуйте если да.
Решение. Да, потому что в данном случае мы имеем дело с вершинами четного порядка.
Слайд 20
Задача 3
В первенстве класса по настольному теннису 6
участников: Андрей, Борис Виктор, Галина, Дмитрий и Елена. Первенство
проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?
Решение:
Построим граф. Сыгранные игры отметим синими линиями, красными дополним до полного графа. Получим, что сыграно 7 игр, а осталось – 8. Можно проверить: в графе 6 вершин тогда всего ребер 6*5/2=15 (7+8).
Слайд 21
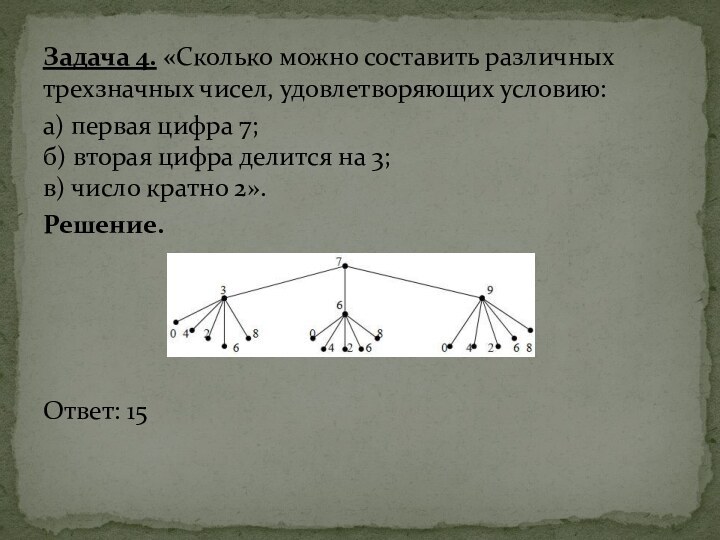
Задача 4. «Сколько можно составить различных трехзначных чисел, удовлетворяющих
условию:
а) первая цифра 7;
б) вторая цифра делится на 3;
в)
число кратно 2».
Решение.
Ответ: 15
Слайд 22
Задача 5.
В стране Цифра есть 9 городов с
названиями 1, 2, 3, 4, 5, 6, 7, 8,
9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли из города 1 добраться в город 9?
Решение. Покажем возможные маршруты, нарисовав граф. И в этой задаче 1 и 9 попали в две разных части графа. Ясно, что в правой части графа сгруппировались города-цифры нацело делящиеся на 3, а в левой части графа ребра соединяют две цифры: одну — делящуюся на 3 с остатком 1, а другую — делящуюся на 3 с остатком 2.
Примечание. Отметим, что один и тот же граф можно нарисовать по-разному. Если учащиеся одного класса нарисуют графы к одной задаче, то мы можем получить столько графов, сколько учащихся их рисовали. Нарисованные по-разному графы (если они нарисованы без ошибок) принято называть изоморфными. Любой читатель может нарисовать бесконечное множество изоморфных графов.
Слайд 23
Правило. Для подсчета числа ребер графа необходимо просуммировать
степени вершин и полученный результат разделить на два.
Следствие. Сумма
степеней всех вершин графа должна быть четной (иначе ее нельзя было бы разделить на 2 нацело).
Теорема. Число нечетных вершин любого графа — четно.
Слайд 24
Задача 6.
В классе 30 человек. Может ли быть
так, что 9 из них имеют по 3 друга
(в этом классе), 11 - по 4 друга, а 10 - по 5 друзей.
Примечание. Если Петя друг Васи, то Вася - друг Пети.
Решение. Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3; 11 — степень 4; 10 - степень 5. Однако у такого графа 19 нечетных вершин, что противоречит теореме.
Слайд 25
Задача 7.
В деревне есть 15 телефонов, а АТС
отсутствует. Можно ли телефоны соединить проводами так, чтобы каждый
телефон был соединен ровно с пятью другими?
Решение. Предположим, что это возможно. Рассмотрим граф, вершины которого соответствуют телефонам, а ребра — соединяющим их проводам. В этом графе
(15 *5) /2 вершин, степень каждой из которой равна пяти. Подсчитаем количество ребер в этом графе. Для этого сначала просуммируем степени всех его вершин. Ясно, что при таком подсчете каждое ребро учтено дважды (оно ведь соединяет две вершины!). Поэтому число ребер графа должно быть равно. Но это число нецелое! Следовательно, такого графа не существует, а значит, и соединить телефоны требуемым образом невозможно.
Слайд 26
Ориентированный граф или орграф называется граф, у которого
множество ребер является множеством упорядоченных пар.
Началом ребра называется вершина,
указанная в паре первой, концом – вторая этой пары (графически она указана стрелкой).
Орграф часто будем обозначать парой (V,E), где V – множество вершин, Е – множество дуг графа. Если дуга е, соединяющая вершины x и y, ориентирована от х и y, то будем говорить, что х – начало дуги и х – конец дуги е, или что дуга е выходит из х и заходит в y. Такую дугу е будем иногда называть (x,y)–дугой.
Вершины x и y будем называть смежными, если существует (x,y)–дуга или (y,x)–дуга. Если дуга е соединяет вершины x и y, то будем говорить, что инцидентна вершинам x и y.
Дугу, выходящую из некоторой вершины и заходящую в ту же вершину, будем называть петлей, а дуги, выходящие из одной и той же вершины и заходящие в одну и ту же вершину, будем называть кратными.
Слайд 27
Определение. Пусть G – орграф. Полустепенью исхода r–(v) вершины v
графа G называется число дуг, выходящих из v, полустепенью
захода r+(v) – число дуг, заходящих в v.
Предложение. Сумма полустепеней исхода всех вершин графа равна суммe полустепеней захода всех вершин.
Слайд 28
Задача 8. Можно ли спроектировать такой город с
односторонним движением на его улицах, чтобы в каждый перекресток
входило по 2 дороги, а выходило по 4 дороги?
Решение. Нет. Сумма положительных полу степеней всех вершин равна сумме отрицательных полу степеней
Слайд 29
Задача 9
В некоторой стране есть столица и еще
100 городов. Некоторые города (в том числе и столица)
соединены дорогами с односторонним движением. Из каждого нестоличного города выходит 20 дорог, и в каждый такой город входит 21 дорога. Докажите, что в столицу нельзя проехать ни из одного города.
Решение
Пусть в столицу входит a дорог. Тогда общее число "входящих" дорог равно 21 · 100 + a, а общее количество "выходящих" дорог не больше 20 · 100 + (100 - a).
Поэтому, 21*100+а≤20*100+(100-а) т.е. 2*а ≤100 Таким образом, a = 0.