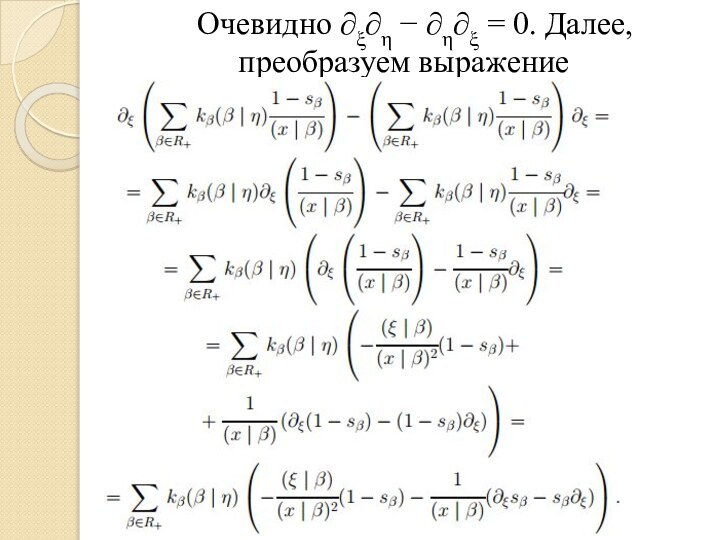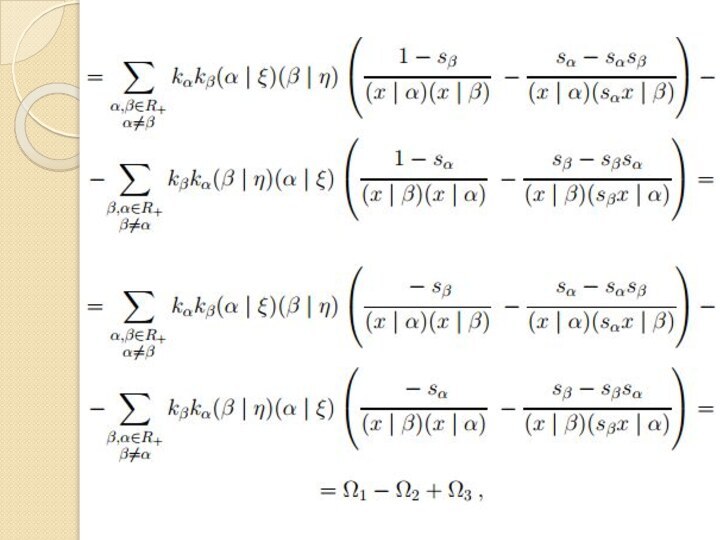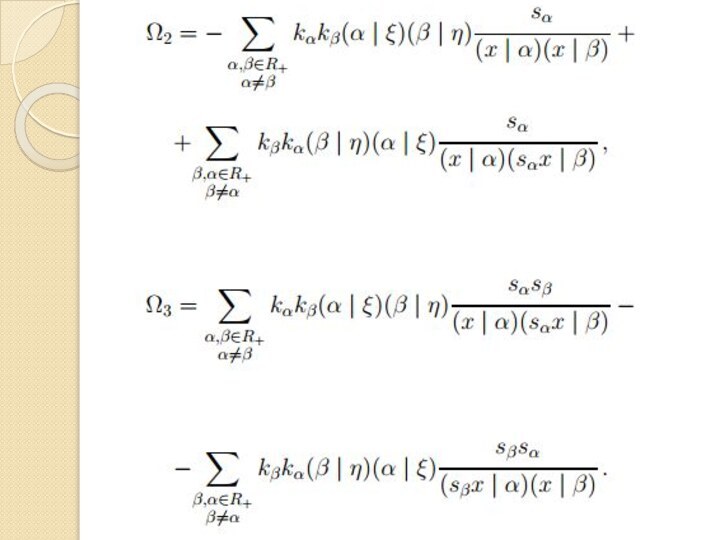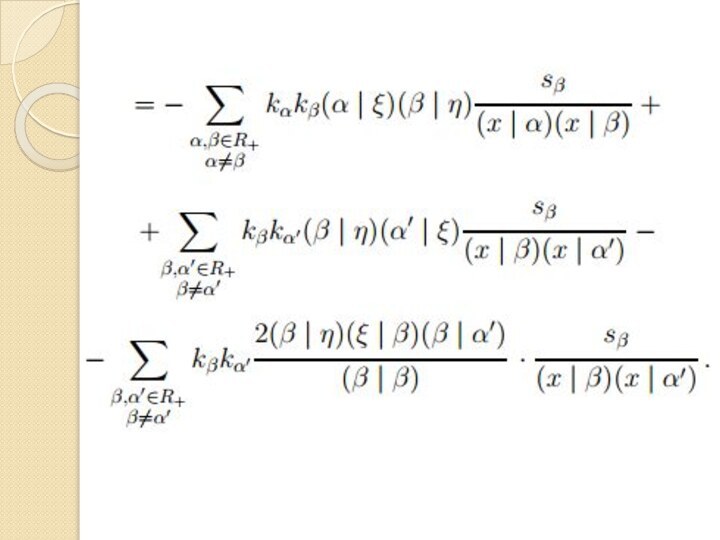относительно композиции.
Теорема 4. Для произвольных ненулевых векторов ξ, η
∈ V соответствующие операторы Дункла коммутируют:TξTη = TηTξ.
Доказательство. Рассмотрим разность
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть