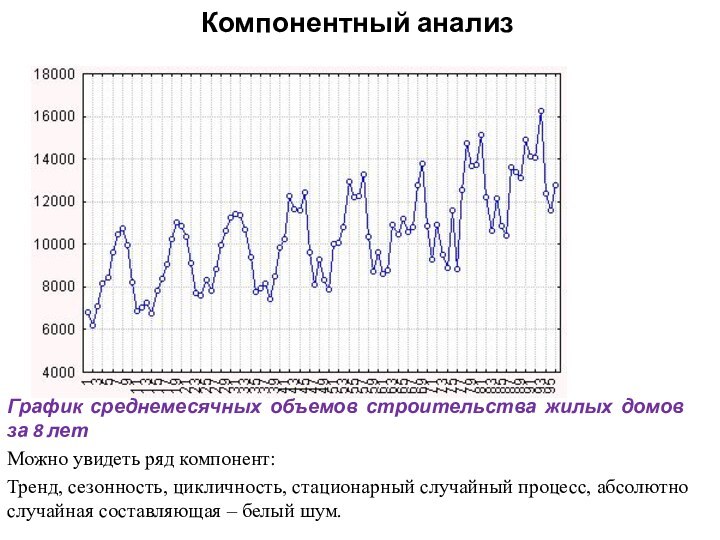
Слайд 2
Тренд
Пусть временной ряд можно представить в виде:
Величина t
- абсолютно случайная составляющая, называемая белым шумом
и удовлетворяющая требованиям:
1) М(t)=0;
2) D(t)=2;
3) cov(t,t+k)=0 при любых t и k0 .
Величина ξt может быть генерирована, либо детерминированной функцией, либо случайным процессом, либо их комбинацией.
Опр. Под детерминированным трендом понимают долговременную тенденцию развития, имеющую вид непериодической неслучайной, медленно изменяющейся функции времени. ξt =f(t)=a0+a1t+a2t2
Случайный (стохастический тренд) ξt =ξt-1
Комбинация трендов ξt =ξt-1 +a0+a1t+a2t2
Детерминированный тренд может быть:
Линейный
Кусочно-линейный
Нелинейный
Слайд 3
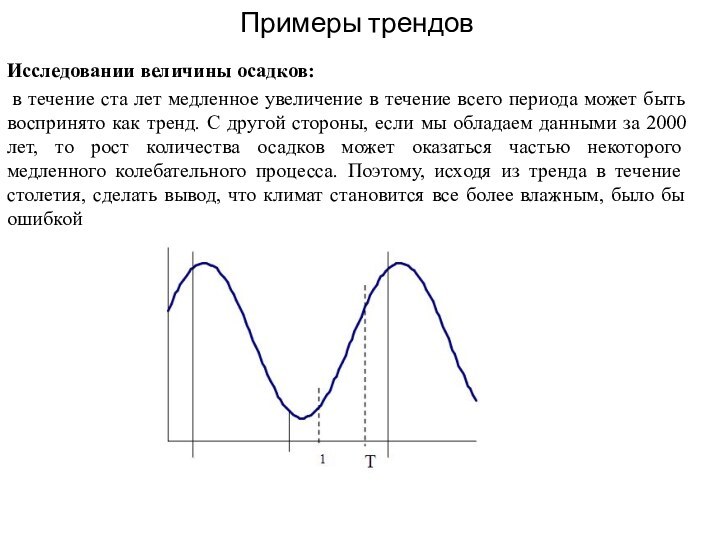
Примеры трендов
Исследовании величины осадков:
в течение ста лет
медленное увеличение в течение всего периода может быть воспринято
как тренд. С другой стороны, если мы обладаем данными за 2000 лет, то рост количества осадков может оказаться частью некоторого медленного колебательного процесса. Поэтому, исходя из тренда в течение столетия, сделать вывод, что климат становится все более влажным, было бы ошибкой
Слайд 4
Примеры трендов
.
Кусочно-линейный тренд
Слайд 5
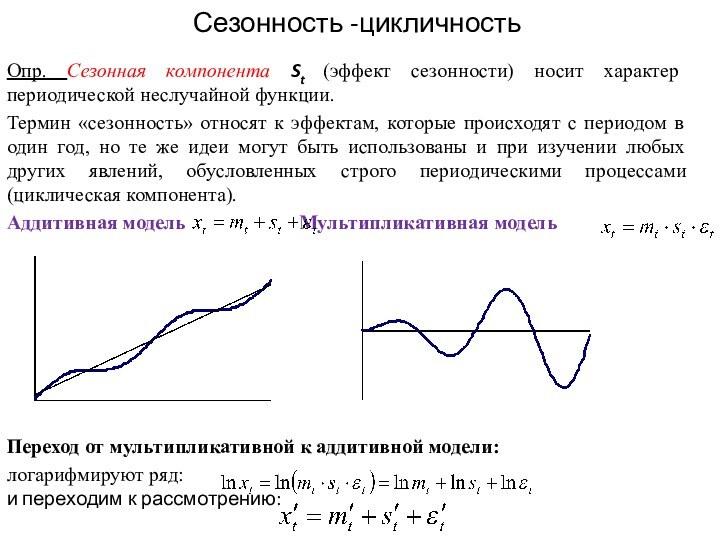
Сезонность -цикличность
Опр. Сезонная компонента St (эффект сезонности) носит
характер периодической неслучайной функции.
Термин «сезонность» относят к эффектам,
которые происходят с периодом в один год, но те же идеи могут быть использованы и при изучении любых других явлений, обусловленных строго периодическими процессами (циклическая компонента).
Аддитивная модель Мультипликативная модель
Переход от мультипликативной к аддитивной модели:
логарифмируют ряд:
и переходим к рассмотрению:
Слайд 6
Определение наличия тренда и сезонной компоненты
Определения наличия тренда
на основе:
Визуального анализа графика исходных данных;
Теоретических предпосылках о наличии
тренда;
Спектрального анализа;
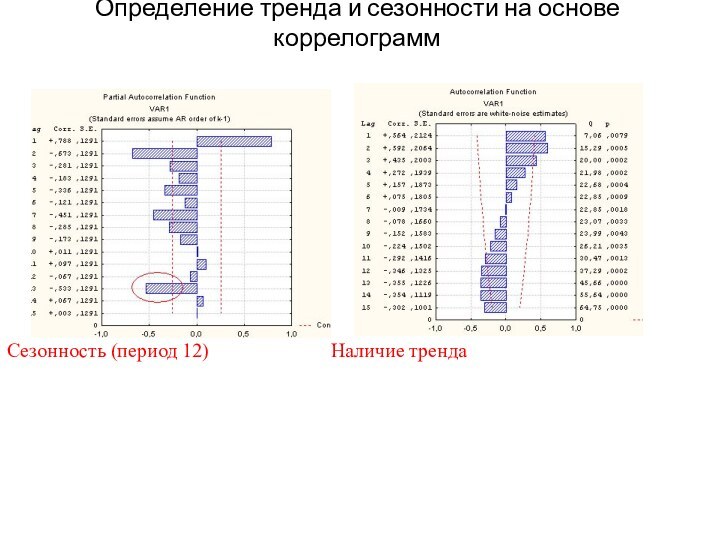
Анализа коррелограмм АКФ и ЧАКФ;
Теста Форестера-Стюарта.
Определения наличия периодической компоненты на основе:
Визуального анализа графика исходных данных;
Теоретических предпосылках о наличии сезонности (цикличности);
Спектрального анализа;
Анализа коррелограмм АКФ и ЧАКФ;
.
Слайд 7
Что такое спектральный анализ?
Ряд Фурье выглядит следующим образом:
Длина периода членов ряда, следующая: первый синусоидальный
член имеет период 2, второй имеет период 2/2=, третий - 2/3 и т.д. Аналогично и для косинусоидальных членов. Вся сумма имеет период 2.
Любую конечную последовательность x1,x2,…xN, не обязательно периодическую, можно представить в виде суммы:
Коэффициенты b0,b1,… b[N/2] и a1,a2,… a[N/2] можно оценить через значение xt и тригонометрические функции.
Если же ряд x1,x2,…xN является периодическим, с периодом T, причем N кратно T, значения xt достаточно представить на множестве 1,2,… T, поскольку xt+T = xt (в силу периодичности последовательности). Разложение Фурье для такой последовательности будет иметь вид:
Слайд 8
Периодограмма и спектрограмма
Опр. График, на котором по оси
ординат отложено rk2, а по оси абсцисс – период
, называется периодограммой.(здесь )
Опр. График, на котором по оси ординат отложено rk2, а по оси абсцисс – частота , называется спектрограммой (спектром).
Спектр является необходимым инструментом при определении периода колебаний периодической компоненты.
Рассмотрим одну тригонометрическую пару в разложении Фурье.
Коэффициенты ak и bk определяются из условия:
Преобразовав выражение, получим:
Слайд 9
Определение наличия периодической составляющей
Если среднее значение временного ряда
равно нулю (т.е. тренда нет), то выражение xt2=(xt-0)2=D(xt) –
есть дисперсия. И в этом случае rk2 показывает вклад тригонометрической пары с периодом в общую дисперсию ряда. Для тригонометрической пары с периодом rk2 показывает степень синхронных колебаний исходного ряда и тригонометрической функции с периодом .
/цикличность
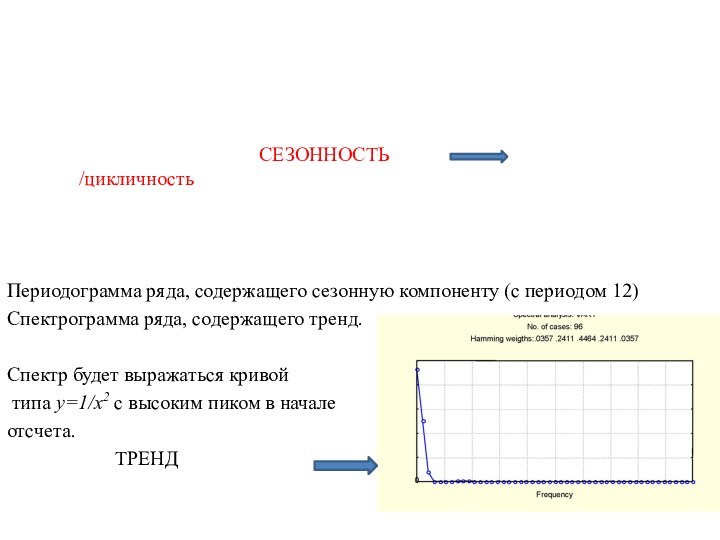
Периодограмма ряда, содержащего сезонную компоненту (с периодом
12)
Спектрограмма ряда, содержащего тренд.
Спектр будет выражаться кривой
типа y=1/x2 с высоким пиком в начале
отсчета.
ТРЕНД
Слайд 11
Что такое коррелограммы
С помощью коэффициентов автокорреляции, можно измерить
связь между текущими и прошлыми значениями исходного временного ряда
(сдвинутую на заданное количество лагов назад переменную называют лаговой) Совокупность коэффициентов автокорреляции образует автокорреляционную функцию (АКФ, (ACF)).
Коэффициент автокорреляции измеряет связь между текущими и прошлыми наблюдениями временного ряда и рассчитывается следующим образом:
где k – количество лагов запаздывания, - среднее значение ряда.
Частный коэффициент автокорреляции измеряет связь между текущим значением переменной Xt и предыдущими значениями этой переменной Xt-1, Xt-2, …, Xt-k, когда влияние всех промежуточных временных лагов устранено.
Частный коэффициент автокорреляции лежит в основе частной автокорреляционной функции (ЧАКФ).
Слайд 12
Что такое коррелограммы
Опр. График автокорреляционной функции, где по
оси абсцисс откладывается k – количество лагов запаздывания, а
по оси ординат соответствующие значения коэффициентов автокорреляции, называется коррелограммой АКФ. Аналогичный график частной автокорреляционной функции называется частной коррелограммой.