Слайд 2
Литература
Грес П.В. Математика для гуманитариев. Учебное пособие. М.:
Университетская книга, Логос, 2006
Суходольский Г.В. Математика для гуманитариев. Харьков:
Изд-во Гуманитарный Центр, 2007
Пилиди В.С. Курс математики для гуманитариев. М.: Вузовская книга, 2006
Слайд 3
Математика для гуманитарных специальностей. Учебно-методический комплекс (для студентов
гуманитарного факультета НГУ). Новосибирск, 2011
http://gf.nsu.ru/www/?page_id=621
Слайд 4
Содержание курса
Часть 1. Логика
Часть 2. Множества, отношения, функции
Часть
3. Комбинаторика и теория вероятностей
Часть 4. Некоторые вопросы информатики
Слайд 5
Традиционная (аристотелевская) логика
Многозначные логики
Слайд 6
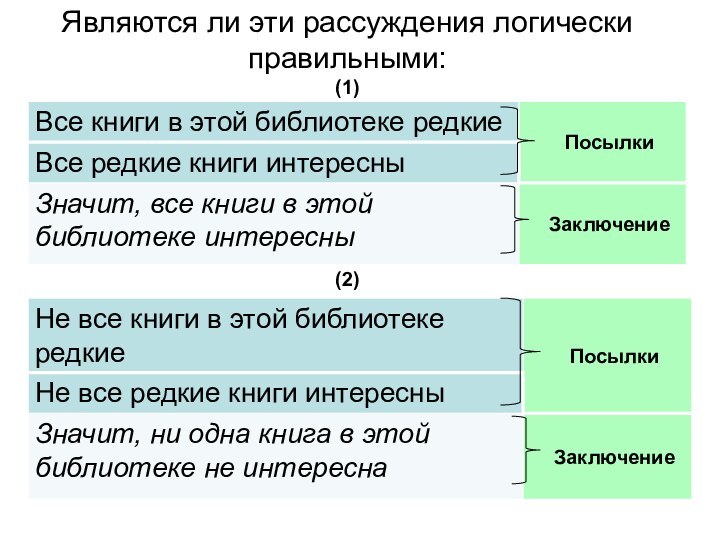
Являются ли эти рассуждения логически правильными:
(1)
(2)
Слайд 7
Пример (1) представляет правильный логический вывод, пример (2)
– неправильный.
Правильный логический вывод сохраняет истинность. Иначе говоря, гарантирует
истинность заключения в том случае, если посылки окажутся истинными.
Если вывод заключения s из посылок p и q логически правилен, то во всех тех ситуациях, когда p и q истинны, истинность s гарантирована.
Слайд 8
Истинность результата логического вывода зависит от того, истинны
ли посылки. Правильность логического вывода от этого не зависит.
Сова
и лисица – птицы
Следовательно, лисица есть птица
Все киты – млекопитающие
Следовательно, все киты – рыбы
Какое из этих рассуждений является правильным логическим выводом?
Слайд 9
Логическая форма (структура)
Рассуждение является логически правильным выводом, если
логическая форма (структура) посылок действительно позволяет вывести заключение, обладающее
данной логической формой (структурой).
Например,
Все s есть p.
Значит, некоторые s есть p.
Этот вывод правилен для любых предложений с данной логической структурой
Слайд 10
Задача логики – исследовать, какие операции над высказываниями
позволяют сохранить истинность, то есть получить из истинных высказываний
истинные высказывания.
Для того чтобы точно и ясно описывать условия истинности высказываний вводятся специальные системы обозначений (языки логики).
Глубина логического анализа высказываний зависит от того, какой логический язык для этого используется. В рамках классической логики возможны два варианта.
Слайд 11
1. Пропозициональная логика (логика высказываний, сентенциональная логика) используется
для анализа логической структуры рассуждения в терминах составляющих его
простых высказываний и логических связей между этими высказываниями.
Внутреннее устройство простых высказываний при этом не учитывается (каждое из них рассматривается как неделимое целое).
Слайд 12
2. Предикатная логика используется для более глубокого анализа
рассуждения, учитывающего не только логические связи между составляющими его
простыми высказываниями, но и внутреннее устройство этих простых высказываний.
Слайд 13
Пропозиции (высказывания)
Одно из базовых понятий языка пропозициональной логики
– пропозиция.
Пропозиция – то состояние дел в мире, о
котором говорится в предложении.
В классической (двузначной) логике пропозиция всегда либо истинна, либо ложна.
Слайд 14
В повседневном языке существуют специальные средства для указания
на пропозиции.
Например, следующие предложения указывают на пропозицию
р:
Мне сказали, что p Я знаю, что p
Они полагают, что p Известно, что p
Слайд 15
Одно и то же предложение в разных случаях
своего использования может выражать разные пропозиции:
Пример:
предложение Сейчас прозвенит
звонок выражает разные пропозиции в зависимости от того, сказано ли оно в университетской аудитории, школе, театре и т.д.
Слайд 16
Разные предложения могут выражать одну и ту же
пропозицию:
Пример:
предложения Сегодня понедельник (сказанное в понедельник) и Вчера был
понедельник (сказанное во вторник) выражают одну и ту же пропозицию (День, на который указывает данное предложение, является понедельником)
Слайд 17
Логические соотношения между простыми высказываниями определяются логическими связками,
для обозначения которых могут использоваться, в частности, следующие языковые
средства:
и, или, следовательно, значит, поскольку, но, так как, если … то и т.д.
Например, Если p и q, то s
Высказывания делятся на простые и сложные (составные).
Слайд 18
Пропозициональная логика
(сентенциональная логика,
логика высказываний)
Синтаксис
1. Словарь:
пропозициональные
переменные: p, q, g, s...
логические связки (логические символы ):
, , ,
Скобки (, )
больше никаких символов в словаре нет
Слайд 19
Названия логических символов:
- конъюнкция (логическое «и»), используется
также символ &,
- дизъюнкция (логическое «или»),
- импликация (логический условный оператор «если …, то …»), используется также символ ,
- отрицание («неверно, что …»)
Слайд 20
2. Правильные выражений языка пропозициональной логики
Любая пропозициональная переменная
является правильным выражением данного языка.
Если и -
произвольные правильные выражения данного языка, то , , , , (), (), (), () - также правильные выражения.
Больше никаких правильных выражений в этом языке нет.
Слайд 21
Описывая синтаксис пропозициональной логики, мы рассматривали все символы
этой логики как не обладающие значением, т.е. семантически пустые.
Чтобы применять эту логику для анализа рассуждений , необходимо определить смыслы логических символов.
Слайд 22
Пропозициональные переменные могут принимать лишь одно из двух
значений «истина» или «ложь». Часто вместо слова «истина» используют
число «1», вместо «ложь» – число «0».
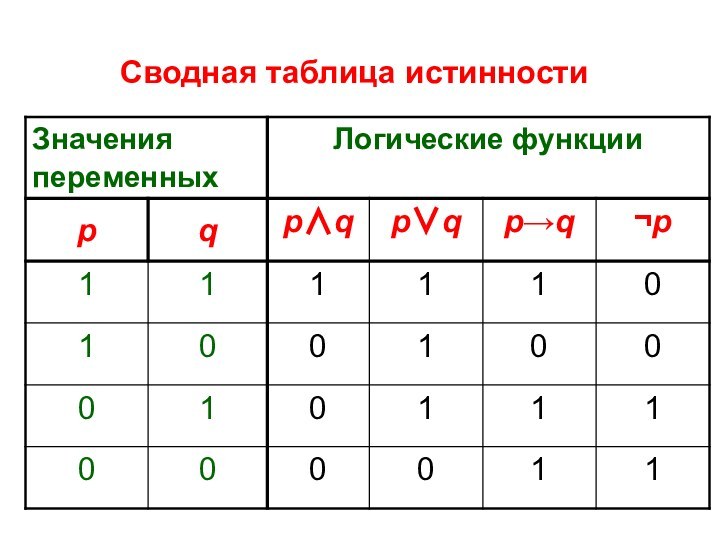
Каждой логической связке ставится в соответствие определённая функция истинности. Эти функции принято задавать в виде таблиц истинности:
Слайд 23
Таблица истинности для конъюнкции
Слайд 24
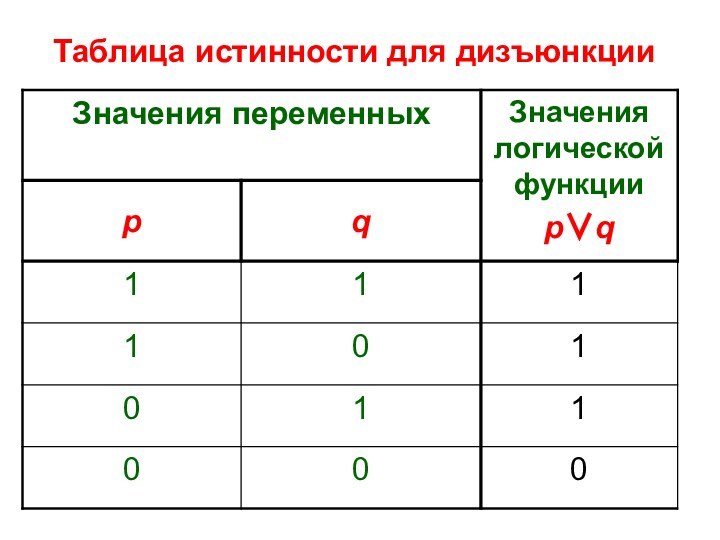
Таблица истинности для дизъюнкции
Слайд 25
Таблица истинности для импликации
Слайд 26
Таблица истинности для отрицания
Слайд 29
В следующих фразах выделите простые пропозиции. Опишите смыслы
фраз посредством языка логики высказываний:
Если завтра будет снег или
завтра будет вьюга, то мы не пойдём на лыжах.
Если в комнате начнут топить, то в ней будет тепло и можно будет ходить без свитера.
Если отзыв рецензента положительный, то редакция примет статью к печати, значит, я смогу отдохнуть.
Слайд 30
Опишите смыслы следующих предложений посредством языка логики высказываний:
Тот,
кто ясно мыслит, ясно говорит.
Сократ – человек и неверно,
что Буцефал - человек
Он – образованный человек и неправда, что у него неважная память.
Если вы были в Париже, то вы видели Лувр или видели Эйфелеву башню.
Тот, кто изучал геометрию, знает теорему Пифагора или слышал о ней, а если эта теорема ему неизвестна, ему нетрудно будет понять её.
Слайд 31
Запишите каждое высказывание с помощью символов пропозициональной логики:
Прозрачный
лес один чернеет, и ель сквозь иней зеленеет, и
речка подо льдом блестит
Если это числительное, то оно обозначает количество предметов или их порядок в некоторой последовательности
Так как мы договорились заранее и установили жёсткие условия, то не представляется никакой возможности не прибыть на место встречи
Слайд 32
Известно, что высказывание «А уважает В, но В
не уважает А» истинно. Исходя из этого, определите истинностные
значения следующих высказываний:
А и В уважают друг друга
А уважает В, или В не уважает А
Либо В не уважает А, либо А уважает В
Неверно, что А и В не уважают друг друга
Если А уважает В, то В уважает А
Если А не уважает В, то В уважает А
Если В не уважает А, то А не уважает В
А уважает В тогда и только тогда, когда В уважает А