Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Л.3. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Содержание

2. Задача геометрических исследований графических моделей конструкций, технологических
3. Если производится, какое либо преобразование некоторой фигуры,
4. О преобразовании мы говорим, когда каждой точке
5. Назовем преобразование обыкновенным, если различным точкам соответствуют
6. Обыкновенным преобразова нием некоторой фигуры является, например,
7. Можно установить соответствие между правым и левым
8. А солнечные лучи, например, осуществляют вырожденное отображение
9. В алгебре теория преобразований тесно связана с
10. Вследствие этого различают, например, преобразования, сохраняющие расстояния,
11. ПРЕОБРАЗОВАНИЯ СОВМЕЩЕНИЯ (СОХРАНЯЮЩИЕ РАССТОЯНИЕ)Преобразование сохраняет расстояние, если
12. Две фигуры могут быть совмещены друг с
13. Совместимые же тела — уже не всегда
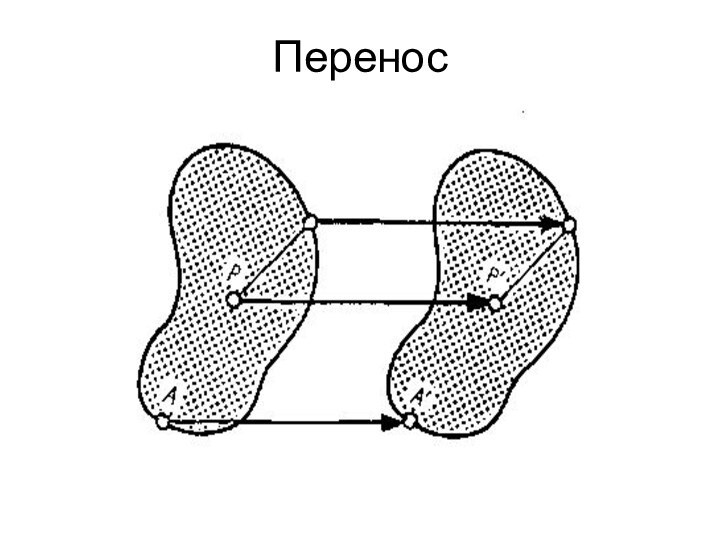
14. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПри параллельном переносе прямые, соединяющие исходные
15. Перенос
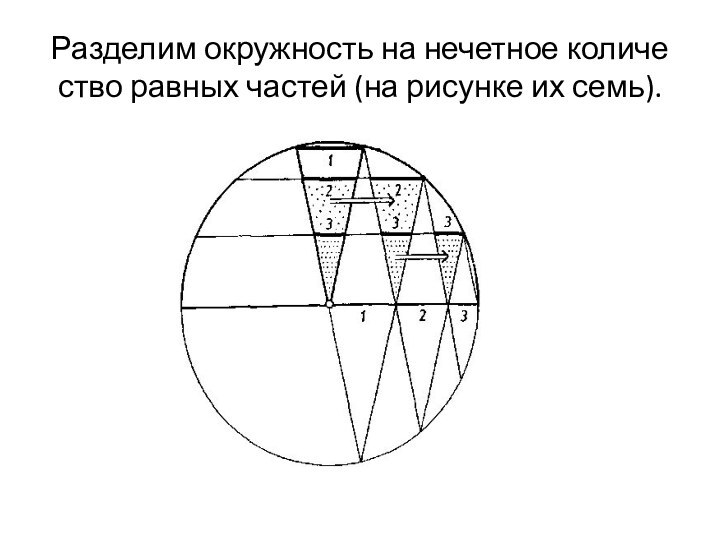
16. Разделим окружность на нечетное количе ство равных частей (на рисунке их семь).
17. Из рисунка видно, что сумма отрезков хорд,
18. При помощи переноса нетрудно убедиться, что отрезки
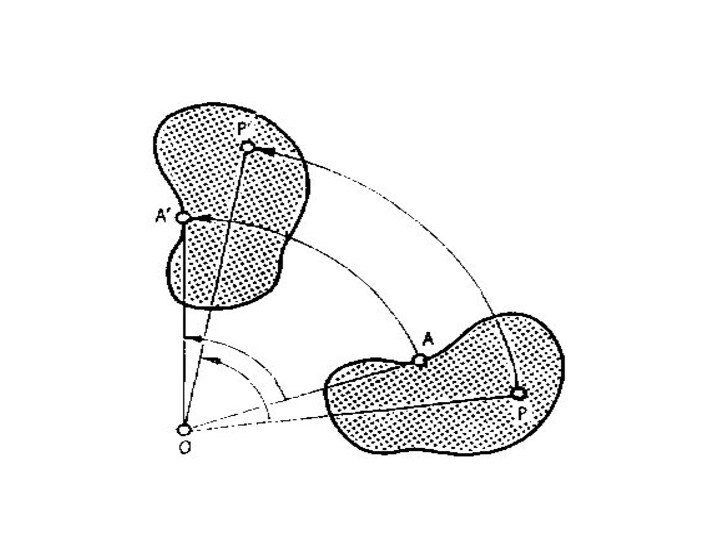
19. ПОВОРОТПоворот (вокруг точки) — это такое преобразование
21. С помощью поворота можно решить, например, следующую
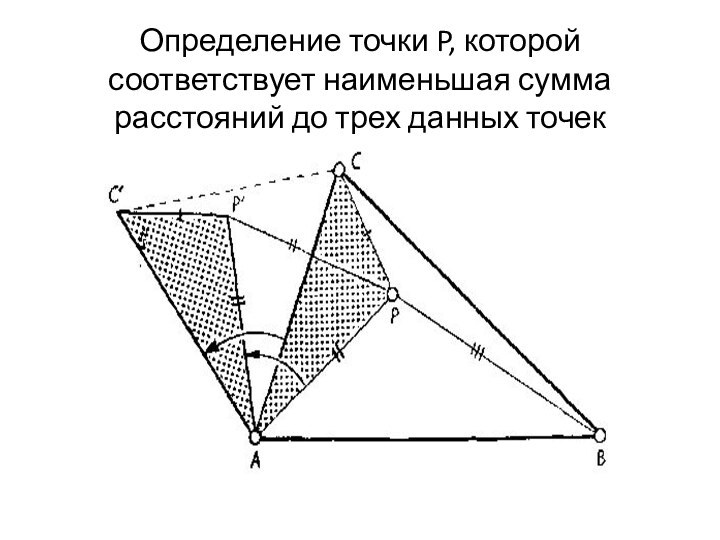
22. Определение точки P, которой соответствует наименьшая сумма расстояний до трех данных точек
23. Этого можно добиться, если, например, повернуть треугольник
24. Сумма отрезков C',P', + P',P + PB
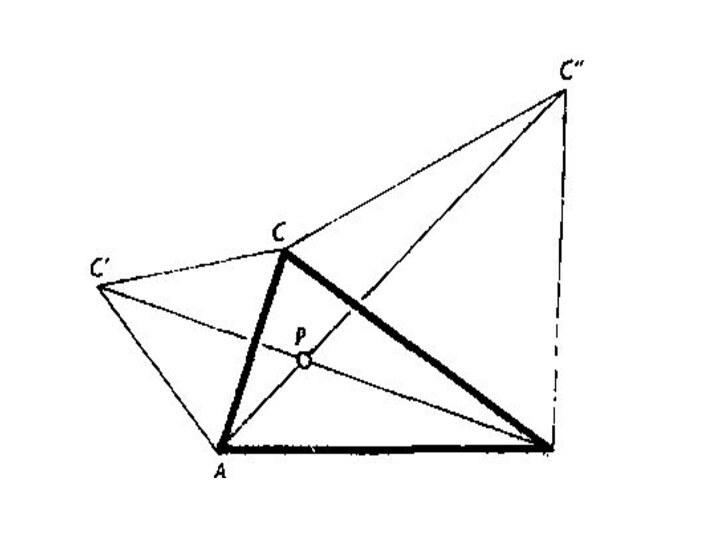
25. Построение изогональной точкиАналогичные соображения позволяют заключить, что
27. Скачать презентацию
28. Похожие презентации

Задача геометрических исследований графических моделей конструкций, технологических процессов и систем управления состоит из установления связи между различными геометрическими фигурами, например, выяснение вопроса, каким образом одна фигура может быть получена из другой, то есть какие преобразования нужно

Главная
Разное
Л.3. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

Задача геометрических исследований графических моделей конструкций, технологических процессов и систем управления состоит

Если производится, какое либо преобразование некоторой фигуры, то интересно исследовать, какие из

О преобразовании мы говорим, когда каждой точке некоторого множества (фигуры) ставится в

Назовем преобразование обыкновенным, если различным точкам соответствуют разные образы. Преобразование, не являющееся

Обыкновенным преобразова нием некоторой фигуры является, например, параллельный перенос. Здесь устанавливается соответствие

Можно установить соответствие между правым и левым ботинками одной пары обуви, каждой

А солнечные лучи, например, осуществляют вырожденное отображение цветка на его тень. В

В алгебре теория преобразований тесно связана с теорией групп. Классификация преобразований осуществляется

Вследствие этого различают, например, преобразования, сохраняющие расстояния, углы, переводящие окружность в окружность,

ПРЕОБРАЗОВАНИЯ СОВМЕЩЕНИЯ (СОХРАНЯЮЩИЕ РАССТОЯНИЕ)Преобразование сохраняет расстояние, если всякому отрезку прямой оно ставит

Две фигуры могут быть совмещены друг с другом, если существует такое преобразование

Совместимые же тела — уже не всегда (например, правый и левый ботинки).

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПри параллельном переносе прямые, соединяющие исходные точки с их образами, параллельны

Разделим окружность на нечетное количе ство равных частей (на рисунке их семь).

Из рисунка видно, что сумма отрезков хорд, расположенных между двумя радиусами равна

При помощи переноса нетрудно убедиться, что отрезки хорд, расположенные между этими радиусами,

ПОВОРОТПоворот (вокруг точки) — это такое преобразование совмещения, при котором неподвижной остается

С помощью поворота можно решить, например, следующую задачу: на плоскости требуется найти

Определение точки P, которой соответствует наименьшая сумма расстояний до трех данных точек

Этого можно добиться, если, например, повернуть треугольник AВC вокруг точки А «во

Сумма отрезков C',P', + P',P + PB равна суммеPA + PB +

Построение изогональной точкиАналогичные соображения позволяют заключить, что точка; Р должна лежать на

Следовательно, искомая точка P является точкой пересечения прямых АС

Слайды презентации

Слайд 2 Задача геометрических исследований графических моделей конструкций, технологических процессов

Задача геометрических исследований графических моделей конструкций, технологических процессов и систем управления

и систем управления состоит из установления связи между различными

геометрическими фигурами, например, выяснение вопроса, каким образом одна фигура может быть получена из другой, то есть какие преобразования нужно произвести с данной фигурой, чтобы получить некоторую другую фигуру.

Слайд 3 Если производится, какое либо преобразование некоторой фигуры, то

Если производится, какое либо преобразование некоторой фигуры, то интересно исследовать, какие

интересно исследовать, какие из свойств фигуры при этом изменяются,

а какие остаются прежними. Всеми этими вопросами занимается теория геометрических преобразований или как говорят математики  теория трансформаций.

Слайд 4 О преобразовании мы говорим, когда каждой точке некоторого

О преобразовании мы говорим, когда каждой точке некоторого множества (фигуры) ставится

множества (фигуры) ставится в соответствие некоторая (другая) точка. Точки,

которые ставятся в соответствие точкам исходного множества, называются образами точек исходного множества при данном преобразовании

Слайд 5 Назовем преобразование обыкновенным, если различным точкам соответствуют разные

Назовем преобразование обыкновенным, если различным точкам соответствуют разные образы. Преобразование, не

образы. Преобразование, не являющееся обыкновенным, называется вырожденным. Преобразования называют

также отображениями.

Слайд 6 Обыкновенным преобразова нием некоторой фигуры является, например, параллельный

Обыкновенным преобразова нием некоторой фигуры является, например, параллельный перенос. Здесь устанавливается

перенос. Здесь устанавливается соответствие между исходными и смещенными положениями

точек. Другой пример: каждой точек кинопленки соответствует одна из точек на экране.

Слайд 7 Можно установить соответствие между правым и левым ботинками

Можно установить соответствие между правым и левым ботинками одной пары обуви,

одной пары обуви, каждой точке одного ботинка можно сопоставить

соответствующую точку другого.

Слайд 8 А солнечные лучи, например, осуществляют вырожденное отображение цветка

А солнечные лучи, например, осуществляют вырожденное отображение цветка на его тень.

на его тень. В действительности, тень от многих точек

цветка падает в одну точку, поэтому соответствие уже не является взаимно однозначным.

Слайд 9 В алгебре теория преобразований тесно связана с теорией

В алгебре теория преобразований тесно связана с теорией групп. Классификация преобразований

групп. Классификация преобразований осуществляется согласно тому, какие из свойств

фигур они оставляют неизменными, то есть какие группы свойств являются инвариантными.

Слайд 10 Вследствие этого различают, например, преобразования, сохраняющие расстояния, углы,

Вследствие этого различают, например, преобразования, сохраняющие расстояния, углы, переводящие окружность в

переводящие окружность в окружность, прямую — в прямую; или

преобразования, сохраняющие свойство непрерывности и другие.

Слайд 11 ПРЕОБРАЗОВАНИЯ СОВМЕЩЕНИЯ (СОХРАНЯЮЩИЕ РАССТОЯНИЕ)
Преобразование сохраняет расстояние, если всякому

ПРЕОБРАЗОВАНИЯ СОВМЕЩЕНИЯ (СОХРАНЯЮЩИЕ РАССТОЯНИЕ)Преобразование сохраняет расстояние, если всякому отрезку прямой оно

отрезку прямой оно ставит в соответствие равный ему отрезок.

Мы назовем такие преобразования совмещениями (преобразованиями совмещения).

Слайд 12 Две фигуры могут быть совмещены друг с другом,

Две фигуры могут быть совмещены друг с другом, если существует такое

если существует такое преобразование совмещения, которое переводит одну из

них в другую.
Совместимые фигуры на плоскости всегда могут быть совмещены друг с другом в результате некоторого движения (для этого, может быть, нужно выйти за пределы чертежа).

Слайд 13 Совместимые же тела — уже не всегда (например,

Совместимые же тела — уже не всегда (например, правый и левый

правый и левый ботинки). Совместимость обозначается знаком =. Ниже

будут рассмотрены некоторые специальные преобразования совмещения на плоскости.

Слайд 14 ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
При параллельном переносе прямые, соединяющие исходные точки

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПри параллельном переносе прямые, соединяющие исходные точки с их образами,

с их образами, параллельны между собой (они задают направление

переноса);
расстояния от исходных точек до их образов равны (длина переноса). Два последовательно выполняемые переноса могут быть заменены одним, который называется их суммой (или произведением).

Слайд 15 Перенос

Слайд 16 Разделим окружность на нечетное количе ство равных частей

(на рисунке их семь).

Слайд 17 Из рисунка видно, что сумма отрезков хорд, расположенных

Из рисунка видно, что сумма отрезков хорд, расположенных между двумя радиусами

между двумя радиусами равна радиусу окружности.
Точки деления, расположенные на

одинаковом расстоянии от диаметра, соединим хордами и проведем радиусы, соответствующие двум средним точкам деления.

Слайд 18 При помощи переноса нетрудно убедиться, что отрезки хорд,

При помощи переноса нетрудно убедиться, что отрезки хорд, расположенные между этими

расположенные между этими радиусами, в сумме дают радиус окружности

(из рисунка видно, что каждый из этих отрезков можно с помощью максимум двух переносов (вместе с соответствующим треугольником) наложить на радиус).

Слайд 19 ПОВОРОТ
Поворот (вокруг точки) — это такое преобразование совмещения,

ПОВОРОТПоворот (вокруг точки) — это такое преобразование совмещения, при котором неподвижной

при котором неподвижной остается только одна точка — центр

вращения.
Поворот однозначно определяется заданием центра вращения, направления и угла, на который совершается поворот.

Слайд 20

Слайд 21 С помощью поворота можно решить, например, следующую задачу:

С помощью поворота можно решить, например, следующую задачу: на плоскости требуется

на плоскости требуется найти точку P, сумма расстояний от

которой до трех данных точек A,B и С той же плоскости была бы наименьшей. Выберем сначала точку P произвольным образом. Величину суммы PA + PB ++ PC можно представить наглядно, если отложить эти отрезки последовательно — один от конца другого.

Слайд 22 Определение точки P, которой соответствует наименьшая сумма расстояний

до трех данных точек

Слайд 23 Этого можно добиться, если, например, повернуть треугольник AВC

Этого можно добиться, если, например, повернуть треугольник AВC вокруг точки А

вокруг точки А «во внешнюю сторону» на 60° (см.

рисунок). При этом получатся равносторонние треугольники ACC', и APP', (оба треугольника равнобедренные с углом при вершине, равным 60°).

Слайд 24 Сумма отрезков C',P', + P',P + PB равна

суммеPA + PB + PC, причем она достигает максимума,

когда все три отрезка лежат на одной прямой. Отсюда следует, что искомая точка P должна лежать на прямой, соединяющей точку В с точкой C', которая является вершиной равностороннего треугольника, построенного на отрезке АС