Презентация на тему Лекция

каждом сообщении символы появляются с известной вероятностью, не зависящей

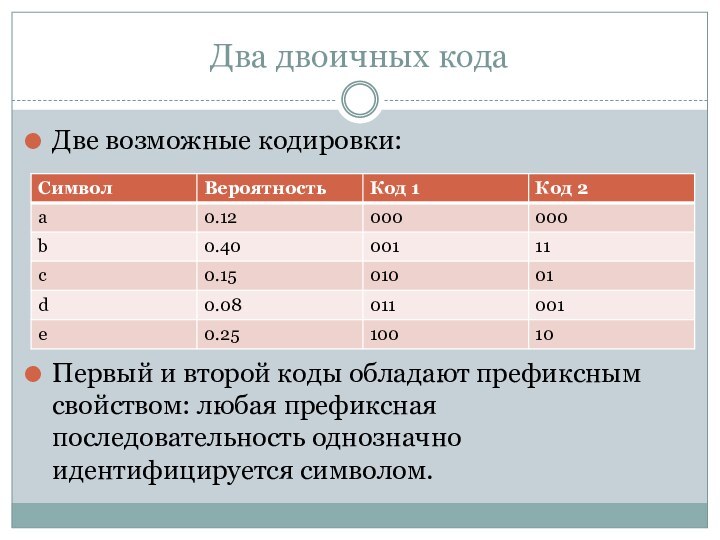
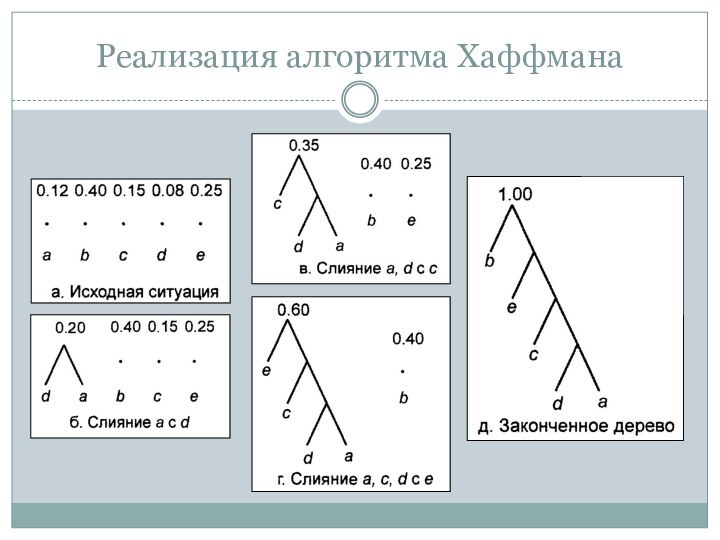
от позиции в сообщении.
Пусть есть сообщение из символов a, b, c, d, e, которые появляются в сообщениях с вероятностями 0.12, 0.4, 0.15, 0.08 и 0.25 соответственно.
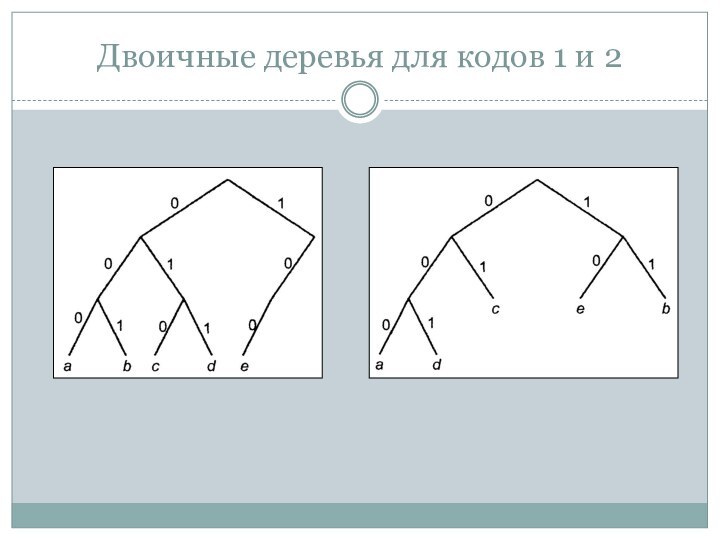
Задача: закодировать каждый символ последовательностью 0 и 1 так, чтобы код любого символа являлся префиксом кода сообщения.
Префиксное свойство позволяет декодировать строку из 0 и 1 путём удаления префиксов (кодов символов) из этой строки.

обладают префиксным свойством: любая префиксная последовательность однозначно идентифицируется символом.

бита
Преобразовать их в символ
Отбросить их. Перейти к шагу 1.
001010011

– bcd.
Алгоритм декодирования для Кода 2:
Определить последовательность битов, однозначно кодирующих символ.
Преобразовать их в символ
Отбросить их. Перейти к шагу 1.
1101001 – bcd.

значения вероятностей их появления в сообщениях, построить такой код

с префиксным свойством, чтобы средняя длина кода (в вероятностном смысле) была минимальной.
Т.е. требуется минимизировать среднюю длину кода, чтобы уменьшить длину сообщения (т.е. сжать сообщение).
Чем короче длина кода символов, тем короче закодированное сообщение. Таким образом, символы с большими вероятностями появления должны иметь более короткие коды.

кода. В этом алгоритме находятся 2 символа a и

b с наименьшими вероятностями появления и заменяются одним фиктивным символом x, который имеет вероятность появления, равную сумме вероятностей появления символов a и b. Затем, использую процедуру рекурсивно находится оптимальный префиксный код для меньшего множества символов (где символы a и b заменены одним символом x).

кодов замещающих символов путем добавления 0 и 1 перед

кодом замещающего символа, и эти два новых кода принимаются как коды заменяемых символов. Например, код символа а будет соответствовать коду символа х с добавленным нулем перед этим кодом, а для кода символа b перед кодом символа х будет добавлена единица.

пути на двоичном дереве: прохождение от узла к его

левому сыну соответствует 0 в коде, а к правому сыну — 1. Если мы пометим листья дерева кодируемыми символами, то получим представление префиксного кода в виде двоичного дерева.
Префиксное свойство гарантирует, что нет символов, которые были бы метками внутренних узлов дерева (не листьев), и наоборот, помечая кодируемыми символами только листья дерева, мы обеспечиваем префиксное свойство кода этих символов.

– деревья, чьи листья помечены кодируемыми символами.
Важный этап

работы алгоритма – выбор из леса двух деревьев с наименьшими весами. Эти два дерева комбинируются в одно с весом, равным сумме весов составляющих деревьев. При слиянии деревьев создается новый узел, который становится корнем объединённого дерева и который имеет в качестве левого и правого сыновей корни старых деревьев. Этот процесс продолжается до тех пор, пока не получится только одно дерево.
Это дерево соответствует коду, имеющему минимальную длину.