Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Лекція: Вектори

Содержание

ПланОсновні визначенняОперації над векторамиВластивості векторівГеометрична інтерпретація
Лекція: «Вектори» Викладач: Мальцев Олександр Михайлович ПланОсновні визначенняОперації над векторамиВластивості векторівГеометрична інтерпретація ВизначенняВектором називають впорядкований набір чиселСкаляр – числова характеристикаНульовой векторСкалярний добуток векторівДовжина вектора Операції над векторамиСума:Множення на скаляр:Лінійна комбінація: Властивості векторівКолінеарність – Ортогональність – Лінійна залежність: , для k,n0 одночасно. Базові задачі1. Довести, що2. Довести, що коли вектори Геометрична інтерпретаціяВектор задає паралельний перенос на площиніДля додавання векторів використовують правило трикутника Геометрична інтерпретаціяКолінеарність ненульових векторів означає їх паралельність.Ортогональність ненульових векторів означає їх перпендикулярність.Якщо Базові задачіНехай АА1 – медіана трикутника ABC. Довести, що Нехай Конец
Слайды презентации

Слайд 2 План
Основні визначення
Операції над векторами
Властивості векторів
Геометрична інтерпретація

ПланОсновні визначенняОперації над векторамиВластивості векторівГеометрична інтерпретація

Слайд 3 Визначення
Вектором називають впорядкований набір чисел

Скаляр – числова характеристика
Нульовой

ВизначенняВектором називають впорядкований набір чиселСкаляр – числова характеристикаНульовой векторСкалярний добуток векторівДовжина

вектор
Скалярний добуток векторів

Довжина вектора

Одиничний вектор – вектор довжини

1.

Слайд 4 Операції над векторами
Сума:
Множення на скаляр:
Лінійна комбінація:

Операції над векторамиСума:Множення на скаляр:Лінійна комбінація:

Слайд 5 Властивості векторів
Колінеарність –
Ортогональність –
Лінійна залежність:

Властивості векторівКолінеарність – Ортогональність – Лінійна залежність: , для k,n0 одночасно.

, для k,n0 одночасно.

Слайд 6 Базові задачі
1. Довести, що


2. Довести, що коли вектори

Базові задачі1. Довести, що2. Довести, що коли вектори та ортогональні, то

та ортогональні,

то

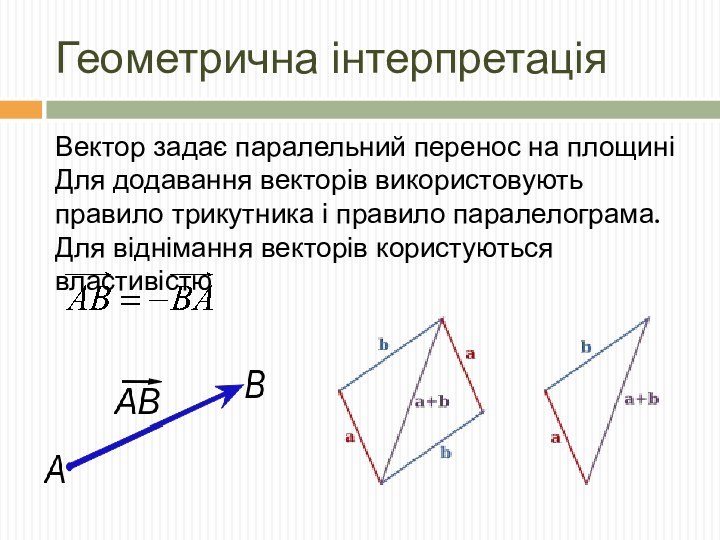
Слайд 7 Геометрична інтерпретація
Вектор задає паралельний перенос на площині
Для додавання

Геометрична інтерпретаціяВектор задає паралельний перенос на площиніДля додавання векторів використовують правило

векторів використовують правило трикутника і правило паралелограма.
Для віднімання векторів

користуються властивістю

Слайд 8 Геометрична інтерпретація
Колінеарність ненульових векторів означає їх паралельність.
Ортогональність ненульових

Геометрична інтерпретаціяКолінеарність ненульових векторів означає їх паралельність.Ортогональність ненульових векторів означає їх

векторів означає їх перпендикулярність.
Якщо два вектори лінійно залежні, то

їх можна перенести на одну пряму.
Якщо два вектори лінійно незалежні, то множина всіх лінійних комбінацій цих векторів задає всі вектори на площині, а ці два вектори называють базісом.
Скалярний добуток:

Слайд 9 Базові задачі
Нехай АА1 – медіана трикутника ABC. Довести,

Базові задачіНехай АА1 – медіана трикутника ABC. Довести, що Нехай

що
Нехай і OA=OB=OC Доведіть, що ABC

– правильний трикутник
  • Имя файла: lektsіya-vektori.pptx
  • Количество просмотров: 114
  • Количество скачиваний: 0
- Предыдущая §Керамические и стеклянные материалы.
Следующая - Наша любимая Хани.

Похожие презентации

Организация прогулок для детей раннего возраста в условиях Крайнего Севера презентация к уроку (младшая группа) Организация прогулок для детей раннего возраста в условиях Крайнего Севера презентация к уроку (младшая группа) 133
Like Like 143
Сенсорное развитие детей презентация к уроку (младшая группа) Сенсорное развитие детей презентация к уроку (младшая группа) 114
презентация Развитие конструктивных способностей и технического творчества презентация презентация Развитие конструктивных способностей и технического творчества презентация 120
ПК 4.2. Предметно-развивающая среда учебного кабинета начальных классов. презентация к уроку по теме ПК 4.2. Предметно-развивающая среда учебного кабинета начальных классов. презентация к уроку по теме 89
МЕМЛЕКЕТТІК БАСҚАРУ МАЗМҰНЫ БОЛАШАҚТЫҢ ҚОСЫМША: МЕМЛЕКЕТТІК БАСҚАРУДЫ МОДЕРНИЗАЦИЯ (Егемен Казахстан, № 70, 12.04.2017 г.) Рухани Жаңғыру Біздің көз алдымызда әлем жаңа, негізінен түсініксіз, тарихи циклді бастайды. Сана мен ойлаудың бұрынғы моделін   МЕМЛЕКЕТТІК БАСҚАРУ МАЗМҰНЫ БОЛАШАҚТЫҢ ҚОСЫМША: МЕМЛЕКЕТТІК БАСҚАРУДЫ МОДЕРНИЗАЦИЯ (Егемен Казахстан, № 70, 12.04.2017 г.) Рухани Жаңғыру Біздің көз алдымызда әлем жаңа, негізінен түсініксіз, тарихи циклді бастайды. Сана мен ойлаудың бұрынғы моделін   136
Техника и приемы общения презентация для интерактивной доски Техника и приемы общения презентация для интерактивной доски 161
Презентация о творчестве И.А.Крылова Презентация о творчестве И.А.Крылова 142
Театрализованная деятельность в детском саду (старшая группа). Презентация. презентация к уроку (старшая группа) Театрализованная деятельность в детском саду (старшая группа). Презентация. презентация к уроку (старшая группа) 116
Презентация к проведению рефлексии в начальной школе Презентация к проведению рефлексии в начальной школе 109
Презентация по казахскому языку на тему Жеті қазына Презентация по казахскому языку на тему Жеті қазына 395
Обмен липидов Обмен липидов 85
Коты-ВоителиЛасточка Коты-ВоителиЛасточка 112
3 puteshestvie v stranu knigi 3 puteshestvie v stranu knigi 87
Презентация для проведения проф. ориентации по специальности Строительство и эксплуатация а/д и аэродромов Презентация для проведения проф. ориентации по специальности Строительство и эксплуатация а/д и аэродромов 106
Проблемы адаптации первоклассников в школе презентация к уроку (1 класс) Проблемы адаптации первоклассников в школе презентация к уроку (1 класс) 135
Организация маркетинговой деятельности. Организация маркетинговой деятельности. 109
Успешная адаптация детей к детскому саду – как фактор эмоционального благополучия. презентация к занятию (младшая группа) по теме Успешная адаптация детей к детскому саду – как фактор эмоционального благополучия. презентация к занятию (младшая группа) по теме 49
ПК 4.2 Предметно-развивающая среда материал по теме ПК 4.2 Предметно-развивающая среда материал по теме 95
Презентация Повышение эффективности и качества реабилитационной работы через использование современных педагогических технологий Презентация Повышение эффективности и качества реабилитационной работы через использование современных педагогических технологий 88
Создание ситуации успеха на уроках в начальной школе материал по теме Создание ситуации успеха на уроках в начальной школе материал по теме 120
Шаблоны презентаций Цветочные Шаблоны презентаций Цветочные 114
Состав поездов Состав поездов 135
Реклама Реклама 137
Петербурговедение , мосты Санкт-Петербурга материал Петербурговедение , мосты Санкт-Петербурга материал 127
проект Моя семья проект (младшая группа) проект Моя семья проект (младшая группа) 118
Ел укытучысы- 2017 учебно-методический материал по теме Ел укытучысы- 2017 учебно-методический материал по теме 112
международные дни для детей презентация по теме международные дни для детей презентация по теме 46
День Знаний в 1 классе День Знаний в 1 классе 134
Гордыня это мое недовольство Гордыня это мое недовольство 114