Слайд 2
Некоторые основные определения
Статистика – это прежде всего способ

мышления, и для ее применения нужно лишь иметь немного
здравого смысла и знать основы математики (Мак-Коннелл). Статистика оперирует понятием «случайный» или «стохастический»
Слово стохастический (от греч. στοχαστικός – «умеющий угадывать») используется во многих терминах из разных областей науки, и в общем означает неопределённость, случайность чего-либо.
Случайная величина – это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
Стохастический процесс – это процесс, поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны, так и случайными. Однако (М. Как, Э. Нельсон) любое развитие процесса во времени (неважно, детерминированное или вероятностное) при анализе в терминах вероятностей будет стохастическим процессом (иными словами, все процессы, имеющие развитие во времени, с точки зрения теории вероятностей, стохастические)
Описательная статистика – описывает, подытоживает и воспроизводит в виде таблиц или графиков данные того или иного распределения, вычисляет среднее для данного распределения, его размах и дисперсию.
Индуктивная статистика – проверяет, можно ли распространить результаты, полученные на данной выборке, на всю популяцию, из которой взята эта выборка. Иными словами - позволяет выяснить, до какой степени можно путем индукции обобщить на большее число объектов ту или иную закономерность, обнаруженную при изучении их ограниченной группы в ходе какого-либо наблюдения или эксперимента.
Популяция («генеральная совокупность» ) в статистике не обязательно означает какую-либо группу людей или естественное сообщество; этот термин относится ко всем объектам, образующим общую изучаемую совокупность
Выборка («выборочная совокупность») – это n-ное количество элементов, отобранных с помощью научных методов так, чтобы она была репрезентативной, т.е. отражала популяцию в целом (n – объем выборки).
Данные в статистике – это основные элементы, подлежащие анализу.
Выделяют 2 группы и 4 шкалы данных:
качественные – номинальные и порядковые
количественные – интервальные (относительные) и отношений (абсолютные) .
Слайд 3
Шкалы представления данных
Номинальная шкала обозначает принадлежность к группе.

Например, М – мужчины, Ж – женщины; КГ –
контрольная группа, ЭГ – экспериментальная группа.
Порядковая шкала – ранжирование объектов по какому-либо признаку. Например, старший ребенок в семье получает номер 1, следующий за ним – номер 2 и т.д.; или лучший спортсмен получает 1-е место, следующий за ним – 2-е место и т. д.
Интервальная (относительная) шкала – данные ранжированы, но интервалы между всеми последовательными величинами равны; здесь обходятся без такой величины, как «истинный» нуль. Например, температурная шкала Цельсия, возраст, календарная хронология. Так нулевой отметке термометра соответствует определенная температура; когда мы появляемся на свет, наш возраст не равен нулю; а эти строки писались в 2012 г. от Рождества Христова, в 7520 г. от сотворения мира и примерно через 12 млрд. лет после образования Солнечной Системы.
Шкала отношений (абсолютная) – включает в себя «истинный» нуль и обладает всеми свойствами других шкал измерения, а также при желании могут быть преобразованы в интервальные, порядковые и номинальные данные. Например, расстояние, высота и промежуток времени. Отметка «нуль сантиметров» указывает на отсутствие расстояния или высоты, а нулевая отметка времени – на то, что еще ничего не произошло.
Слайд 4
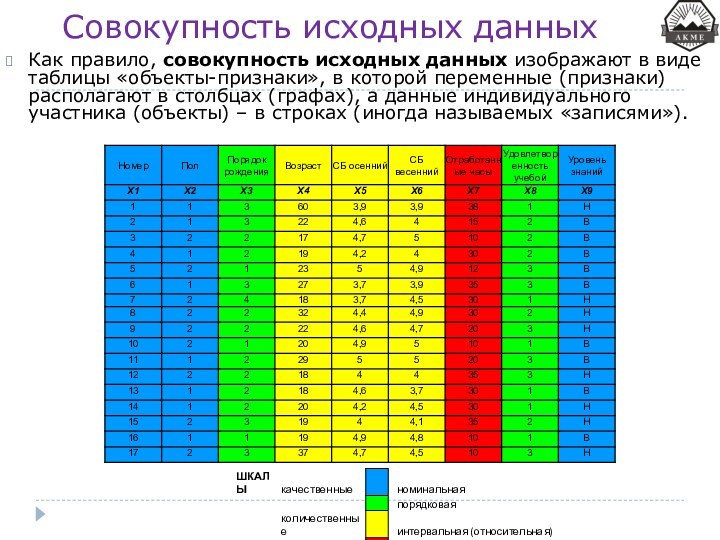
Совокупность исходных данных
Как правило, совокупность исходных данных изображают
в виде таблицы «объекты-признаки», в которой переменные (признаки) располагают
в столбцах (графах), а данные индивидуального участника (объекты) – в строках (иногда называемых «записями»).
Слайд 6
Распределение Distribution
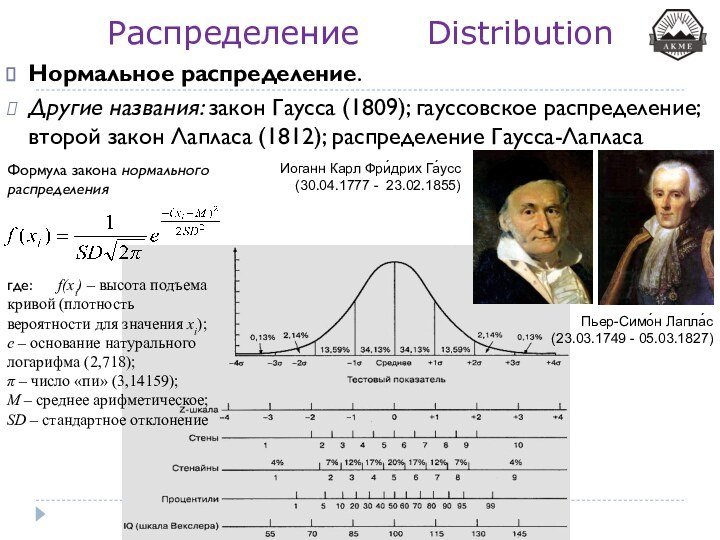
Нормальное распределение.
Другие названия: закон
Гаусса (1809); гауссовское распределение; второй закон Лапласа (1812); распределение
Гаусса-Лапласа
Формула закона нормального распределения
где: f(xi) – высота подъема кривой (плотность вероятности для значения xi); е – основание натурального логарифма (2,718);
π – число «пи» (3,14159);
М – среднее арифметическое; SD – стандартное отклонение
Иоганн Карл Фри́дрих Га́усс (30.04.1777 - 23.02.1855)
Пьер-Симо́н Лапла́с (23.03.1749 - 05.03.1827)
Слайд 7
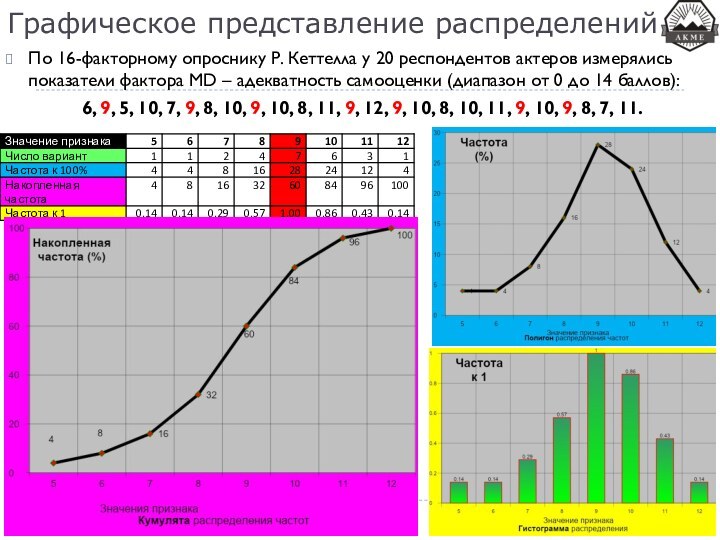
Графическое представление распределений
По 16-факторному опроснику Р. Кеттелла у
20 респондентов актеров измерялись показатели фактора MD – адекватность
самооценки (диапазон от 0 до 14 баллов):
6, 9, 5, 10, 7, 9, 8, 10, 9, 10, 8, 11, 9, 12, 9, 10, 8, 10, 11, 9, 10, 9, 8, 7, 11.