Слайд 2
Для полного сжигания 1 кг углерода С требуется 1,866 м3 кислорода О2,

в результате чего образуется 1,866 м3 двуокиси углерода СО2 и выделяется 34
МДж (34 000 кДж) теплоты: С + О2 = СО2 + Q. Для полного сгорания 1 кг серы S требуется0,7 м3 кислорода О2, в результате образуется 0,7 м3 сернистого газа SО2 и выделяется 10,5 МДж теплоты: S + О2 = SО2 +Q. Для полного сгорания 1 кг водорода Н2 требуется 5,6 м3 кислорода О2, образуется 11,2 м3 водяного пара Н2О и выделяется 121,5 МДж теплоты: 2Н2 + О2 = 2Н2О + Q.
Если органическое котельное топливо сгорает полностью, то дымовые газы содержат углекислый газ СО2, сернистый газ SО2, азот топлива и воздуха N2, неиспользованный при горении кислород О2 воздуха, водяной пар Н2О, полученный за счет окисления водорода топлива, испарения влаги, содержащейся в топливе и внесенной с влажным воздухом и при распылении жидкого топлива (в паромеханических форсунках). Чтобы котельное топливо могло сгореть полностью необходимы: достаточное количество воздуха; хорошее перемешивание воздуха с топливом; высокая температура в топке (не менее 700 °С на выходе); достаточное время пребывания топлива и окислителя в топке; постоянный отвод продуктов сгорания из топки.
Если же органическое котельное топливо сгорает не полностью, то образуются вредные для человека и окружающей среды оксиды азота (NО, NО2), серы (SО2), углерода СО (угарный газ), а также сажа, которая осаждается на экранных и конвективных трубах, снижает теплопередачу от топочных газов к теплоносителю, что приводит к уменьшению КПД и перерасходу топлива. Кроме того, сажа может самовозгораться, что приводит к авариям.
Полнота сгорания топлива определяется двумя способами: с помощью газоанализаторов – по показаниям состава уходящих топочных газов оценивается полнота сгорания и избыток воздуха; визуально – по цвету пламени и дыма. При полном сгорании цвет пламени в разогретой топке голубовато-фиолетовый или прозрачно-соломенный, а цвет дыма – бесцветный, прозрачный, невидимый для глаза – летом и светло-серый или белый – зимой. При неполном сгорании цвет пламени оранжево-красный, с темными язычками, непрозрачный, а цвет дыма – серый ближе к темному, непрозрачный. Энтальпия воздуха и продуктов сгорания зависит от объема, теплоемкости и температуры компонентов горения и вычисляется по формулам, после чего строится график зависимости энтальпии от температуры топочных газов для каждого элемента котла (топки, газоходов, пароперегревателя, экономайзера и т.п.).
Слайд 3
Для полного сгорания 1 м3 метана СН4 требуется 9,52 м3 воздухаVо, образуется 10,52 м3 дымовых

газов, содержащих СО2 и водяные пары Н2О, и выделяется 36,5
МДж теплоты: СН4 + 2О2 = СО2 + 2Н2О+ Q.
При окислении 1 м3 метана образуются углекислый газ, водяные пары и 36 МДж теплоты; этана – 63,8 МДж, пропана – 91,4 МДж, бутана – 120 МДж и т.д. Природный газ, который, также как и сжиженный, газовая котельная может применять в ходе работы, не имеет цвета, запаха, вкуса, легче воздуха (плотность 0,75 кг/м3). Теплота сгорания 33…40 МДж/м3. Природный газ на человека действует удушающе, а смертельная доза – 25 % от объема помещения. Температура воспламенения в воздухе – это температура, которую должен иметь газ или газовое топливо, чтобы начался самопроизвольный процесс горения за счет выделения теплоты горящими частицами газа без подвода теплоты извне. Для метана температура воспламенения в воздухе 654…790 °С. При концентрации природного газа более 17 % – он огнеопасен.
Для того чтобы своевременно обнаружить утечки, газовая котельная вполне может столкнуться с такой проблемой, горючие газы подвергают одоризации, т.е. придают им резкий специфический запах. Газы одорируют после их очистки и осушки перед поступлением в магистральный газопровод в одоризационных установках при помощи одоранта – этилмеркаптана, в количестве 16 г на 1000 м3 природного газа. Одоризация считается эффективной, если наличие газа в воздухе может быть обнаружено при концентрации его, равной 1/5 от нижнего предела взрываемости. Это значит, что одоризация газа, имеющего нижний предел взрываемости 5 %, будет достаточной, если запах его хорошо ощутим в воздухе помещения при концентрации газа в нем 1 %. Основные требования к одоранту: должен мгновенно растворяться в газах и сгорать, не образовывая вредных для человека соединений; не должен взаимодействовать с влагой и вызывать коррозию труб и оборудования.
Сжиженный газ имеет плотность 2,6 кг/м3 (т.е. тяжелее воздуха в 1,5 раза), теплоту сгорания 110…120 МДж/м3, предел взрываемости 1,5…9,5 % от объема помещения (при наличии искры), температуру вспышки 750…850 °С. Зимняя смесь состоит из 75 % пропана и 25 % бутана, летняя – 25 % пропана и 75 % бутана. Одорант (этилмеркаптан) используется в количестве 40 г на 1000 м3 газа, для того чтобы ощутить запах при концентрации 0,5 % от объема помещения.
Слайд 4
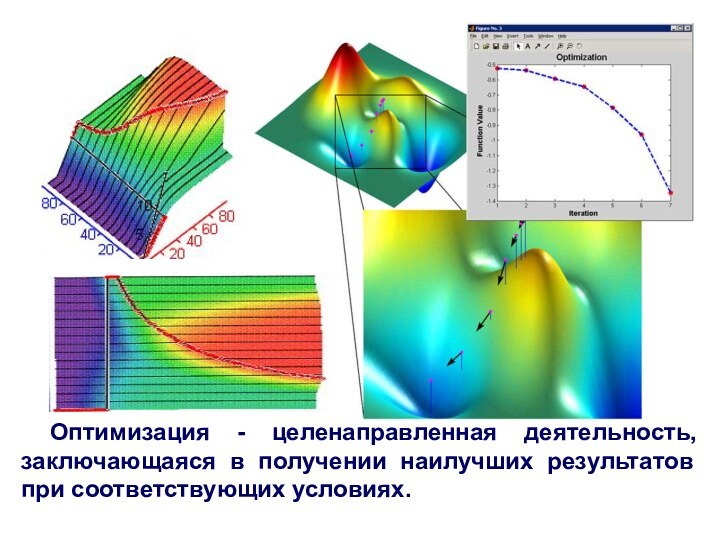
Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших
результатов при соответствующих условиях.
Слайд 5
Поиски оптимальных решений привели к созданию специальных математических
методов и уже в 18 веке были заложены математические
основы оптимизации (вариационное исчисление, численные методы и др).
Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно.
Особенно большие трудности возникали при решении задач оптимизации химических процессов (например, горение топлива) из-за большого числа параметров и их сложной взаимосвязи между собой.
Слайд 6
Постановка задачи оптимизации предполагает существование конкурирующих свойств процесса,
например:
количество продукции - "расход сырья";
количество продукции - "качество продукции".
Выбор
компромиссного варианта для указанных свойств и представляет собой процедуру решения оптимизационной задачи.
Слайд 7
При постановке задачи оптимизации необходимо:
1. Наличие объекта оптимизации

и цели оптимизации. При этом формулировка каждой задачи оптимизации
должна требовать экстремального значения лишь одной величины, т.е. одновременно системе не должно приписываться два и более критериев оптимизации, т.к. практически всегда экстремум одного критерия не соответствует экстремуму другого. Типичный пример неправильной постановки задачи оптимизации: "Получить максимальную производительность при минимальной себестоимости". Ошибка заключается в том, что ставится задача поиска оптимума 2-х величин, противоречащих друг другу по своей сути.
Правильная постановка задачи могла быть следующая: получить максимальную производительность при заданной себестоимости или получить минимальную себестоимость при заданной производительности. В первом случае критерий оптимизации - производительность, а во втором - себестоимость.
2. Наличие ресурсов оптимизации, под которыми понимают возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен обладать определенными степенями свободы - управляющими воздействиями.
3. Возможность количественной оценки оптимизируемой величины, поскольку только в этом случае можно сравнивать эффекты от выбора тех или иных управляющих воздействий.
4. Учет ограничений.
Слайд 8
Математическое моделирование
в энергетике
Постановка оптимизационных задач.
Критерии оптимальности.
Виды
ограничений
Слайд 9
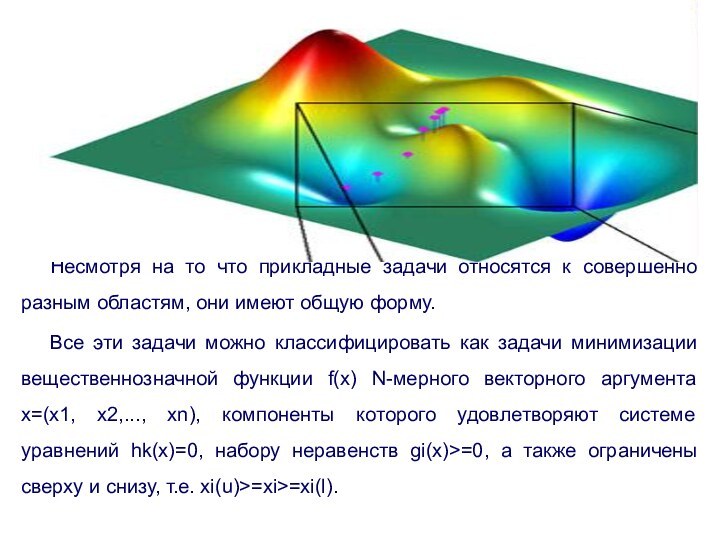
Несмотря на то что прикладные задачи относятся к
совершенно разным областям, они имеют общую форму.
Все эти
задачи можно классифицировать как задачи минимизации вещественнозначной функции f(x) N-мерного векторного аргумента x=(x1, x2,..., xn), компоненты которого удовлетворяют системе уравнений hk(x)=0, набору неравенств gi(x)>=0, а также ограничены сверху и снизу, т.е. xi(u)>=xi>=xi(l).
Слайд 10
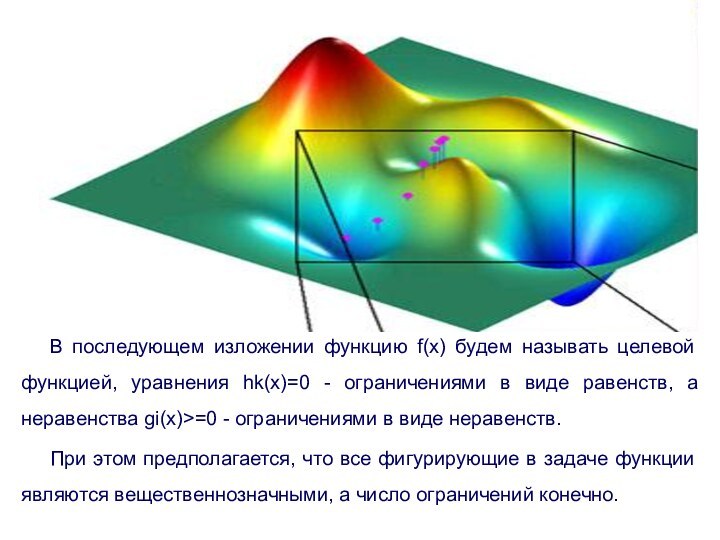
В последующем изложении функцию f(x) будем называть целевой
функцией, уравнения hk(x)=0 - ограничениями в виде равенств, а
неравенства gi(x)>=0 - ограничениями в виде неравенств.
При этом предполагается, что все фигурирующие в задаче функции являются вещественнозначными, а число ограничений конечно.
Слайд 11
Оптимизационная задача общего вида:
минимизировать f(x)
при ограничениях:
hk(x)=0, k=1, ...,
K,
gj(x)>=0 j=1, ..., J,
xi(u)>=xi>=xi(l), i=1, ..., N
называется
задачей оптимизации с ограничениями или задачей условной оптимизации.
Задача, в которой нет ограничений, т.е.
J=K=0;
xi(u)= - xi(l) = бесконечности, i=1, ..., N,
называется оптимизационной задачей без ограничений или задачей безусловной оптимизации.
Слайд 12
Критерии оптимальности
Обычно оптимизируемая величина связана с экономичностью работы

рассматриваемого объекта (аппарат, энергоблок, ТЭС).
Оптимизируемый вариант работы объекта должен
оцениваться какой-то количественной мерой - критерием оптимальности.
Критерием оптимальности называется количественная оценка оптимизируемого качества объекта.
На основании выбранного критерия оптимальности составляется целевая функция, представляющая собой зависимость критерия оптимальности от параметров, влияющих на ее значение.
Вид критерия оптимальности или целевой функции определяется конкретной задачей оптимизации.
Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.
Наиболее общей постановкой оптимальной задачи является выражение критерия оптимальности в виде экономической оценки (производительность, себестоимость продукции, прибыль, рентабельность).
Однако в частных задачах оптимизации, когда объект является частью технологического процесса, не всегда удается или не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта.
Слайд 13
В таких случаях критерием оптимальности может служить технологическая
характеристика, косвенно оценивающая экономичность работы агрегата (время контакта, выход
продукта, степень превращения, температура).
Например устанавливается оптимальный температурный профиль, длительность цикла - "реакция - регенерация". Но в любом случае любой критерий оптимальности имеет экономическую природу.
Рассмотрим более подробно требования, которые должны предъявляться к критерию оптимальности.
Критерий оптимальности должен выражаться количественно.
Критерий оптимальности должен быть единственным.
Критерий оптимальности должен отражать наиболее существенные стороны процесса.
Желательно чтобы критерий оптимальности имел ясный физический смысл и легко рассчитывался.
Слайд 14
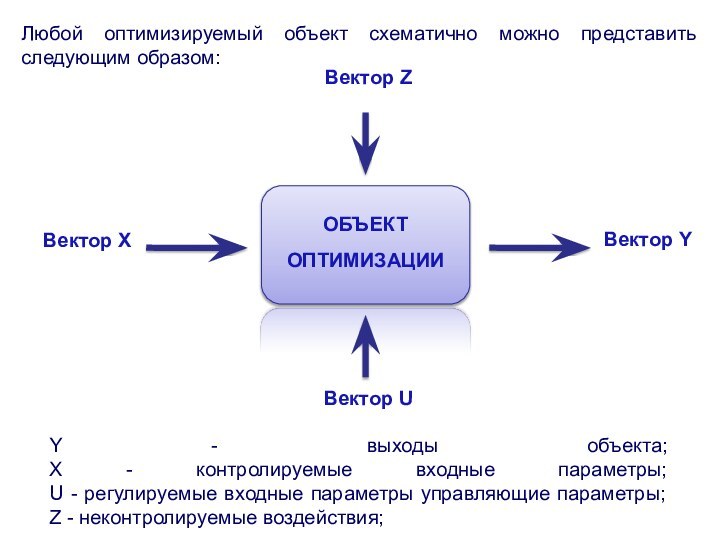
Любой оптимизируемый объект схематично можно представить следующим образом:
Y
- выходы объекта;
X - контролируемые входные параметры;
U
- регулируемые входные параметры управляющие параметры;
Z - неконтролируемые воздействия;
Вектор Z
Вектор Х
Вектор Y
Вектор U
Слайд 15
При постановке конкретных задач оптимизации критерий оптимальности должен
быть записан в виде аналитического выражения.
В том случае,
когда случайные возмущения невелики и их воздействие на объект можно не учитывать, критерий оптимальности может быть представлен как функция входных, выходных и управляющих параметров:
R=R(X1, X2,...,XN, Y1,Y2,...,YN, U1,U2,..., UN);
Слайд 16
Так как Y=f (U), то при фиксированных Х
можно записать:
R=R(Ui)
При этом всякое изменение значений управляющих параметров
двояко сказывается на величине критерия оптимальности:
прямо, т.к управляющие параметры непосредственно входят в выражение критерия оптимизации;
косвенно - через изменение выходных параметров процесса, которые зависят от управляющих.
Если же случайные возмущения достаточно велики и их необходимо учитывать, то следует применять экспериментально - статистические методы, которые позволят получить модель объекта в виде функции
Y=j(Xi,Ui)
которая справедлива только для изученной локальной области. Тогда критерий оптимальности примет следующий вид:
R=R(U,X)
Слайд 17
В принципе, для оптимизации вместо математической модели можно
использовать и сам объект, однако оптимизация опытным путем имеет
ряд существенных недостатков:
необходим реальный объект;
необходимо изменять технологический режим в значительных пределах, что не всегда возможно;
длительность испытаний и сложность обработки данных.
Слайд 18
Наличие математической модели (при условии, что она достаточно
надежно описывает процесс) позволяет значительно проще решить задачу оптимизации
аналитическим либо численным методами.
В задачах оптимизации различают простые и сложные критерии оптимизации.
Критерий оптимальности называется простым, если требуется определить экстремум целевой функции без задания условий на какие-либо другие величины.
Такие критерии обычно используются при решении частных задач оптимизации (например, определение максимальной концентрации целевого продукта, оптимального времени пребывания реакционной смеси в аппарате и т.п.).
Слайд 19
Критерий оптимальности называется сложным, если необходимо установить экстремум
целевой функции при некоторых условиях, которые накладываются на ряд
других величин (например, определение максимальной производительности при заданной себестоимости, определение оптимальной температуры при ограничениях по термостойкости и др.).
Процедура решения задачи оптимизации обязательно включает, помимо выбора управляющих параметров, еще и установление ограничений на эти параметры (термостойкость, взрывобезопасность, мощность перекачивающих устройств).
Слайд 20
Ограничения могут накладываться как по технологическим, так и
по экономическим соображениям.
Итак, для решения задачи оптимизации необходимо:
а) составить
математическую модель объекта оптимизации:
Y=f(X,U)
б) выбрать критерий оптимальности и составить целевую функцию:
R=fi(Y)=F(X,U)
в) установить возможные ограничения, которые должны накладываться на переменные:
fi(X,U)=0
fi(X,U)<0
г) выбрать метод оптимизации, который позволит найти экстремальные значения искомых величин.
Слайд 21
Принято различать задачи статической оптимизации для процессов, протекающих
в установившихся режимах, и задачи динамической оптимизации.
В первом случае
решаются вопросы создания и реализации оптимальной модели процесса, во втором - задачи создания и реализации системы оптимального управления процессом при неустановившихся режимах эксплуатации.
Слайд 22
Математическое моделирование
в энергетике
Классификация оптимизационных задач
Слайд 23
Задачи оптимизации можно классифицировать в соответствии с видом
функций f, hk, gi и размерностью вектора x. Задачи
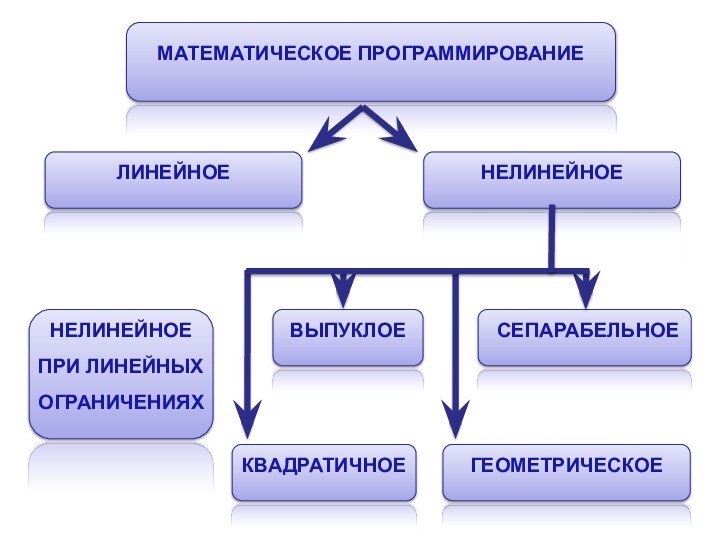
без ограничений, в которых x представляет собой одномерный вектор, называются задачами с одной переменной и составляют простейший, но вместе с тем весьма важный подкласс оптимизационных задач. Задачи условной оптимизации, в которых функции hk, и gi являются линейными, носят название задач с линейными ограничениями.
Слайд 24
В таких задачах целевые функции могут быть либо
линейными, либо нелинейными.
Задачи, которые содержат только линейные функции
вектора непрерывных переменных x, называются задачами линейного программирования; в задачах целочисленного прграммирования компоненты вектора x должны принимать только целые значения.
Задачи с нелинейной целевой функцией и линейными ограничениями называют задачами нелинейного программирования с линейными ограничениями.
Если f(x) - квадратичная функция, то мы имеем дело с задачей квадратичного программирования; если f(x) есть отношение линейных функций, то соответствующая задача носит название задачи дробно - линейного программирования, и т.д.
Деление оптимизационных задач на эти классы представляет значительный интерес, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов их решения.
Слайд 25
Безусловная минимизация функций: В этом случае область задания
функции Q - все n-мерное евклидово пространство, т. е.
на переменные функции ограничений не накладывается вообще. Очевидно, что минимум функции (если он существует) всегда находится внутри ее области задания, поскольку последняя просто не имеет границ.
Минимизация функций при ограничениях в виде равенств: Область задания функции W-бесконечное множество-решений системы уравнений, представляющее собой p-мерную поверхность в n-мерном пространстве.
Поскольку любая точка х принадлежащая W лежит на поверхности fi(х)=0 (i=1, ..., m) и, следовательно, является граничной, то и минимум (в случае его существования) также лежит на границе области W.
Слайд 26
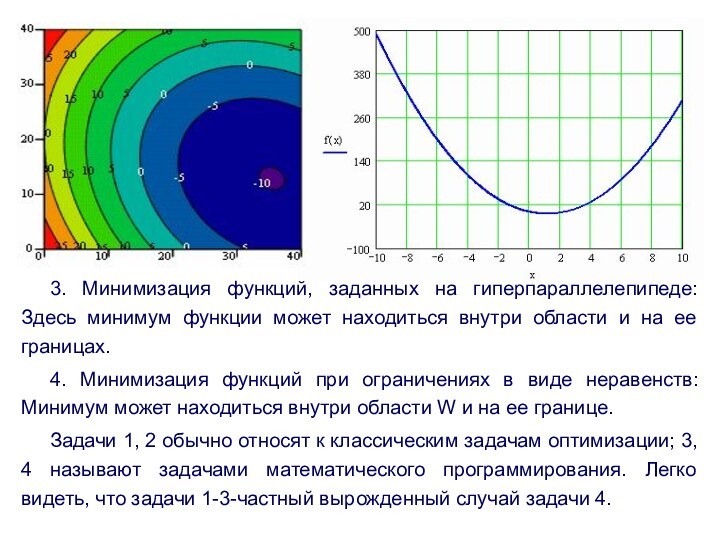
3. Минимизация функций, заданных на гиперпараллелепипеде: Здесь минимум
функции может находиться внутри области и на ее границах.
4. Минимизация функций при ограничениях в виде неравенств: Минимум может находиться внутри области W и на ее границе.
Задачи 1, 2 обычно относят к классическим задачам оптимизации; 3, 4 называют задачами математического программирования. Легко видеть, что задачи 1-3-частный вырожденный случай задачи 4.
Слайд 28
Методы безусловной оптимизации делятся на методы одномерной и
многомерной оптимизации.
МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ
Несмотря на то, что безусловная оптимизация
функции одной переменной наиболее простой тип оптимизационных задач, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения.
Это связано с тем, что задачи однопараметрической оптимизации достаточно часто встречаются в инженерной практике и, кроме того, находят свое применение при реализации более сложных итерактивных процедур многопараметрической оптимизации.
Своеобразным индикатором важности методов оптимизации функции одной переменной является огромное множество реализованных алгоритмов, которые условно можно сгруппировать следующим образом:
методы исключения интервалов:
- метод половинного деления;
- метод "золотого" сечения;
- метод Фибоначчи;
методы полиномиальной аппроксимации;
методы с использованием производных.
Слайд 29
Математическое моделирование
в энергетике
Метод половинного деления
Слайд 30
Метод половинного деления
Требуется найти min W(x) на отрезке
[a,b].
Шаг 1. xm=(a+b)/2; L=b-a; вычислить W(xm).
xm=(2+10)/2=6; L=10-2=8; W(xm)=100.
a
b
L
xm
Слайд 31
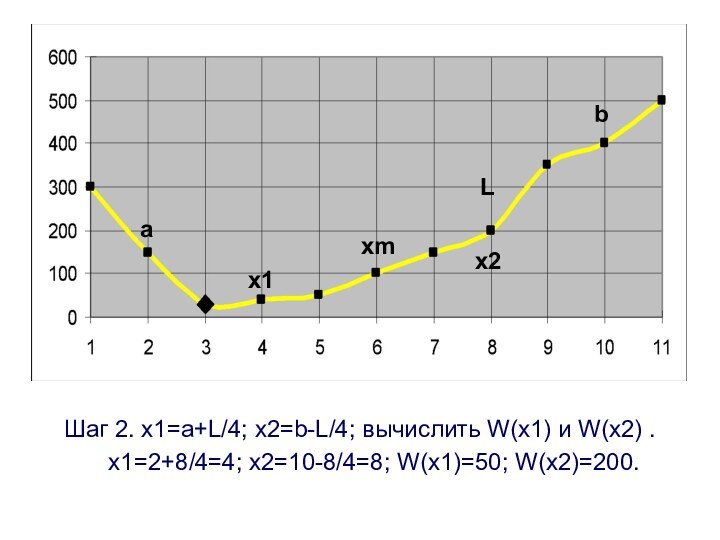
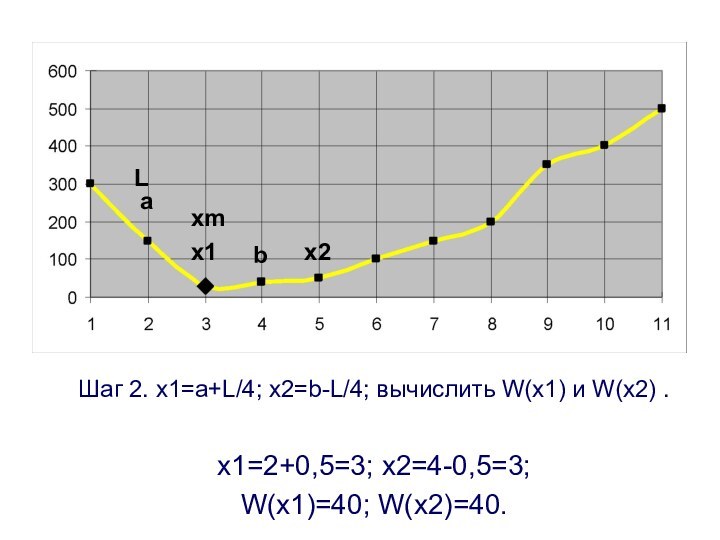
Шаг 2. x1=a+L/4; x2=b-L/4; вычислить W(x1) и W(x2)
.
x1=2+8/4=4; x2=10-8/4=8; W(x1)=50; W(x2)=200.
a
b
L
xm
x1
x2
Слайд 32
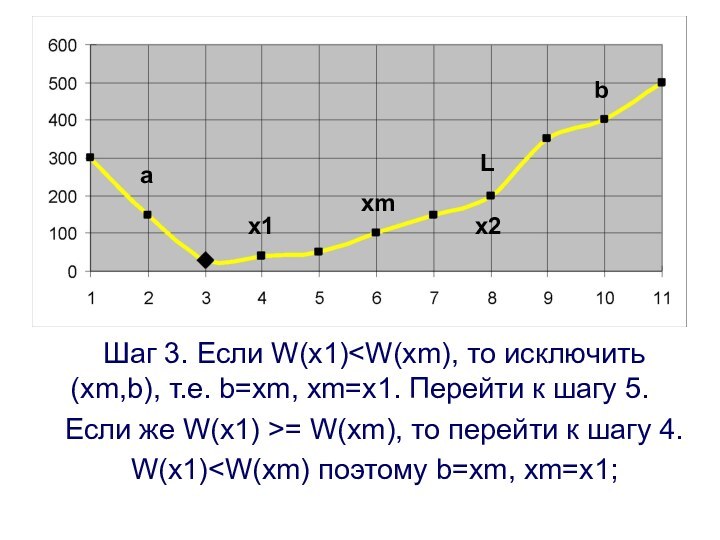
Шаг 3. Если W(x1)
b=xm, xm=x1. Перейти к шагу 5.
Если же W(x1)
>= W(xm), то перейти к шагу 4.
W(x1)
a
b
L
xm
x1
x2
Слайд 33
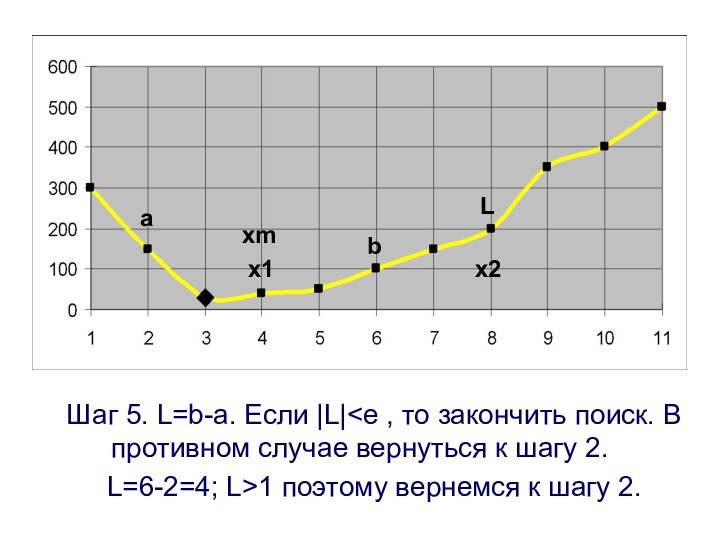
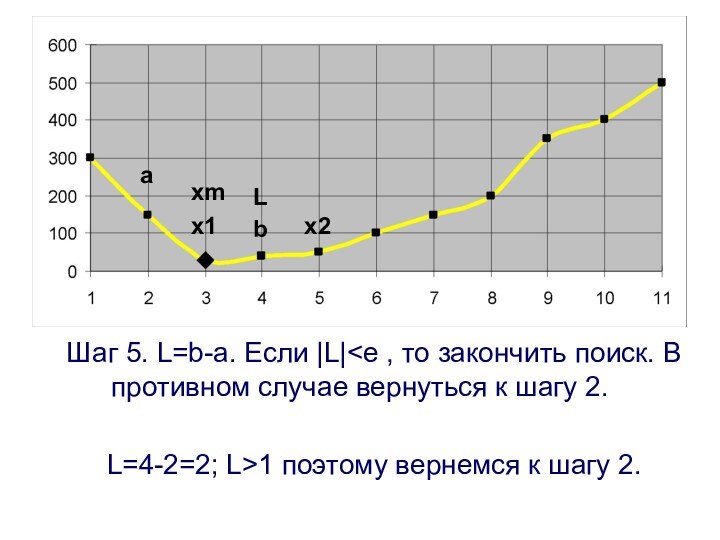
Шаг 5. L=b-a. Если |L|
поиск. В противном случае вернуться к шагу 2.
L=6-2=4;
L>1 поэтому вернемся к шагу 2.
a
b
L
xm
x1
x2
Слайд 34
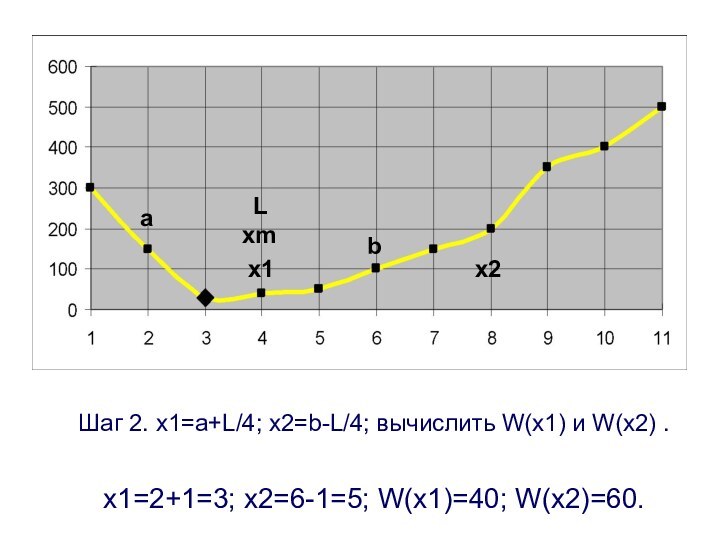
Шаг 2. x1=a+L/4; x2=b-L/4; вычислить W(x1) и W(x2)
.
x1=2+1=3; x2=6-1=5; W(x1)=40; W(x2)=60.
a
b
L
xm
x1
x2
Слайд 35
Шаг 3. Если W(x1)
b=xm, xm=x1. Перейти к шагу 5.
Если же W(x1)
>= W(xm), то перейти к шагу 4.
W(x1)
и переходим к шагу 5.
a
b
L
xm
x1
x2
Слайд 36
Шаг 5. L=b-a. Если |L|
поиск. В противном случае вернуться к шагу 2.
L=4-2=2;
L>1 поэтому вернемся к шагу 2.
a
b
L
xm
x1
x2
Слайд 37
Шаг 2. x1=a+L/4; x2=b-L/4; вычислить W(x1) и W(x2)
.
x1=2+0,5=3; x2=4-0,5=3;
W(x1)=40; W(x2)=40.
a
b
L
xm
x1
x2
Слайд 38
Шаг 3. Если W(x1)
b=xm, xm=x1. Перейти к шагу 5.
Если же W(x1)
>= W(xm), то перейти к шагу 4.
W(x1)=W(xm) поэтому переходим к шагу 4.
a
b
L
xm
x1
x2
Слайд 39
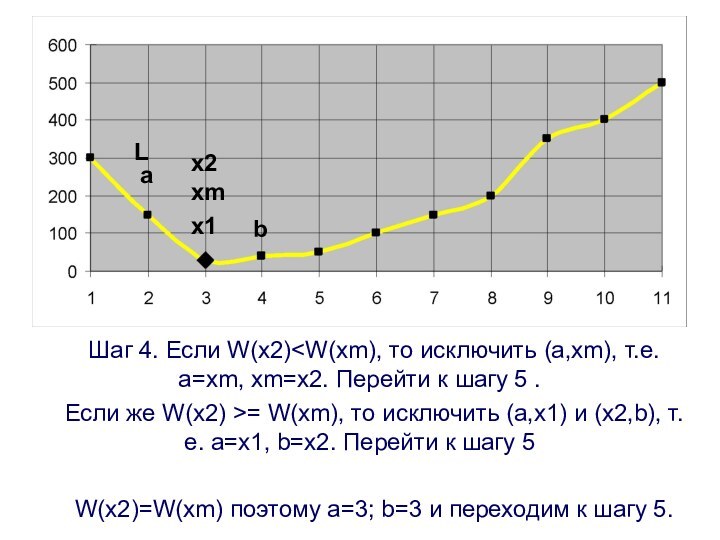
Шаг 4. Если W(x2)
a=xm, xm=x2. Перейти к шагу 5 .
Если же W(x2)
>= W(xm), то исключить (a,x1) и (x2,b), т.е. a=x1, b=x2. Перейти к шагу 5
W(x2)=W(xm) поэтому a=3; b=3 и переходим к шагу 5.
a
b
L
xm
x1
x2
Слайд 40
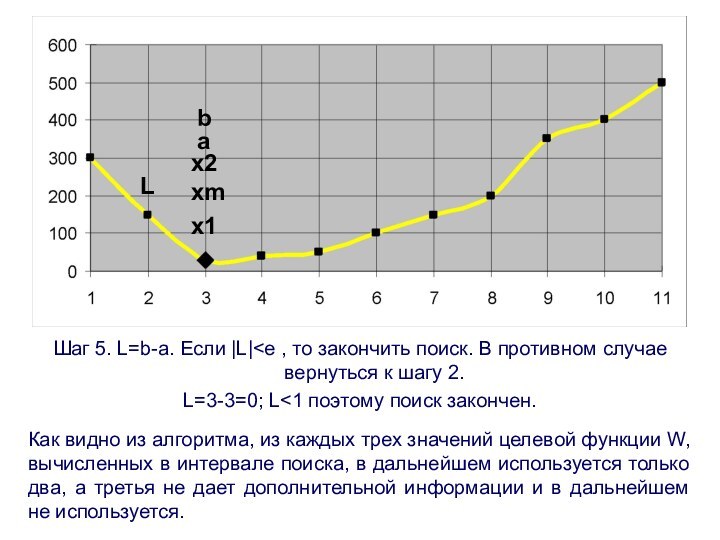
Шаг 5. L=b-a. Если |L|
поиск. В противном случае вернуться к шагу 2.
L=3-3=0;
L<1 поэтому поиск закончен.
Как видно из алгоритма, из каждых трех значений целевой функции W, вычисленных в интервале поиска, в дальнейшем используется только два, а третья не дает дополнительной информации и в дальнейшем не используется.
a
b
L
xm
x1
x2
Слайд 41
ЛИТЕРАТУРА:
Акулич И.Л. Математическое программирование в примерах и задачах: Учеб.
пособие для студентов вузов. — М.: Высшая школа, 1986.
Гилл Ф.,
Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. - М.: Мир, 1985.
Жиглявский А.А., Жилинкас А.Г. Методы поиска глобального экстремума. — М.: Наука, Физматлит, 1991.
Карманов В.Г. Математическое программирование. — Изд-во физ.-мат. литературы, 2004.
Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
Максимов Ю.А.,Филлиповская Е.А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
Максимов Ю.А. Алгоритмы линейного и дискретного программирования. — М.: МИФИ, 1980.





















![Математическое моделированиев энергетикеТема:Горение органических топлив Метод половинного деленияТребуется найти min W(x) на отрезке [a,b].Шаг 1. xm=(a+b)/2; L=b-a;](/img/tmb/14/1301174/aecd7feed50e193c919f2bf7b856da50-720x.jpg)