- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему МЕХАНИКА ТЕЧЕНИЯ ЖИДКОСТИ
Содержание
- 2. Основные виды движения жидкостиУстановившееся движение жидкостиНеустановившееся движение жидкостиРазличают напорные и безнапорные течения жидкости
- 3. Основные понятия струйчатого движенияТраекторией жидкой частицы называют
- 4. Касательная кривая, проведенная к векторам движения частиц
- 5. Малый замкнутый контур образованный линиями тока
- 6. 1) скорости и площади поперечных сечений струек
- 7. Методы изучения движения жидкости В гидромеханике существуют
- 8. Метод ЭйлераМетод Эйлера основан на изучении поля
- 9. Расход жидкостиОбъем жидкости V, проходящей через живое
- 10. Уравнение неразрывности для элементарной струйкиПоток жидкости есть
- 11. Закон неразрывности потокаСхема потока1S1v1= 2S2v2=iSivi=constгде v1, v2,
- 12. Дифференциальная форма уравнения неразрывности или
- 13. Уравнение неразрывности при постоянной плотности При =constили в краткой форме
- 14. Уравнения движения идеальной жидкостиПроекциями отнесенной к массе
- 15. Уравнение Эйлера в развернутом виде
- 16. В векторной форме вышезаписанные уравнения запишутся в
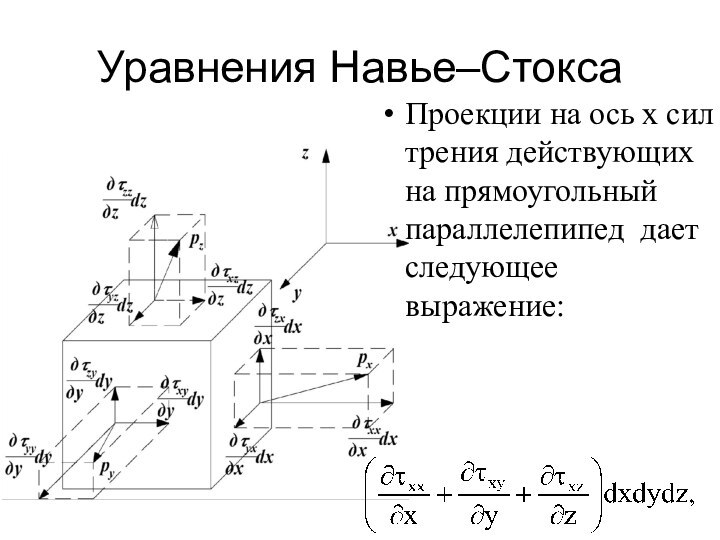
- 17. Уравнения Навье–СтоксаПроекции на ось x сил трения действующих на прямоугольный параллелепипед дает следующее выражение:
- 18. Используя закон Ньютона τ=μ·Δv/Δl , проекции
- 20. Уравнение Навье-Стокса
- 21. В векторной формегде – орты осей
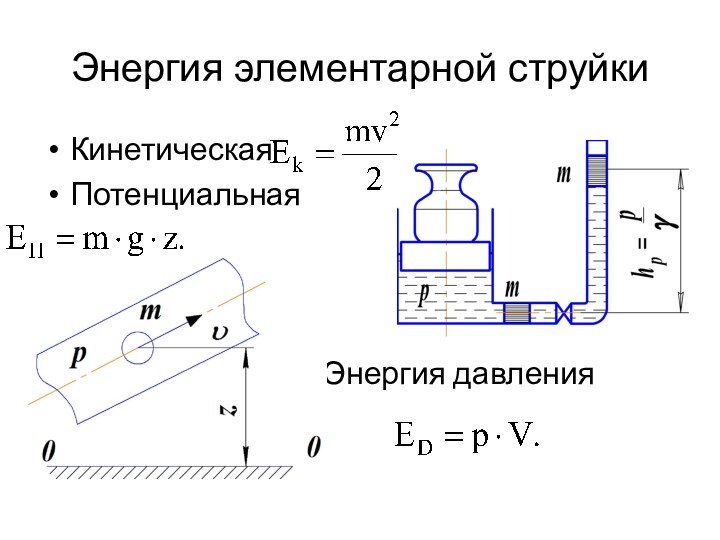
- 22. Энергия элементарной струйкиКинетическаяПотенциальная
- 23. Полная механическая энергия Так как
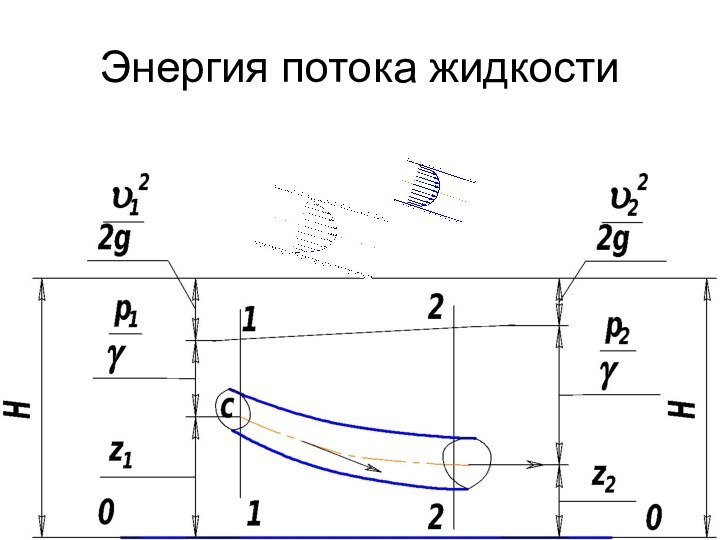
- 24. Энергия потока жидкости
- 25. Полная удельная энергия потокаОпределим слагаемые правой части:кинетическая
- 26. Коэффициент Кориолиса – коэффициент Кориолиса, учитывающего неравномерность
- 27. Потенциальная энергияи полная удельная энергияЕсли использовать зависимость то
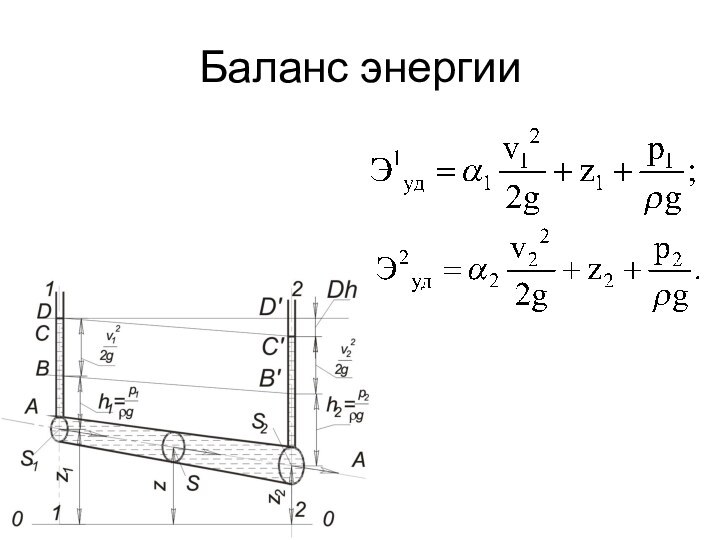
- 28. Баланс энергии
- 29. Уравнение Бернулли для реального потока жидкостиЗдесь
- 30. Физический смысл уравнения Физический (энергетический) смысл уравнения
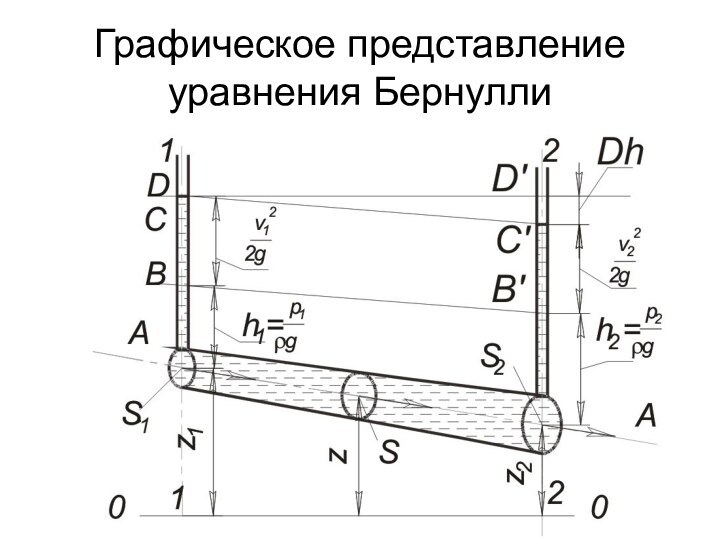
- 32. Графическое представление уравнения Бернулли
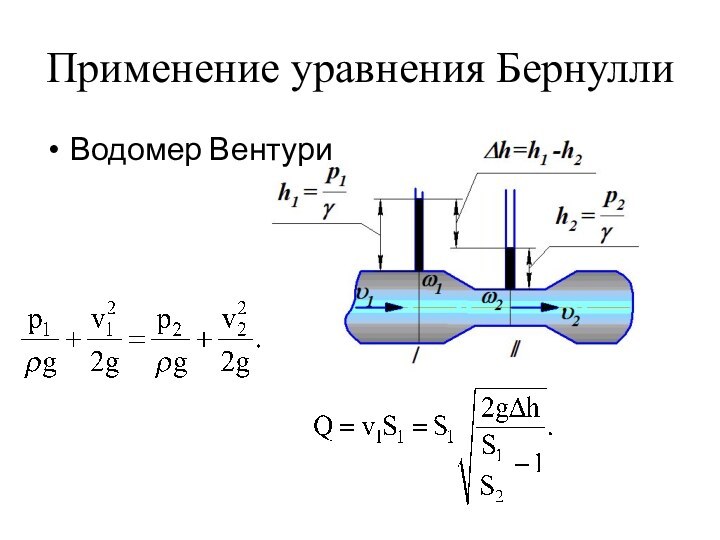
- 33. Применение уравнения Бернулли Водомер Вентури
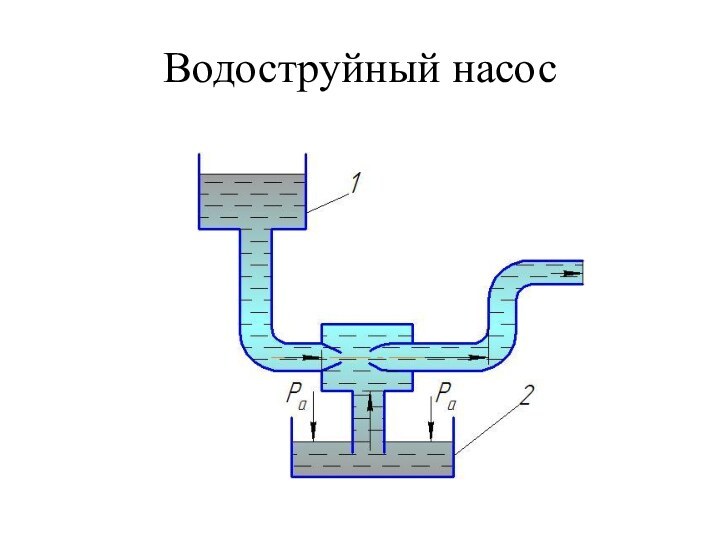
- 34. Водоструйный насос
- 35. Трубка ПитоПолный напор трубки Пито, h1=(p/g)+v2/(2g)пьезометрический напор
- 36. Формула Торричеллигде – коэффициент расхода (истечения),
- 37. Трубка Прандтля
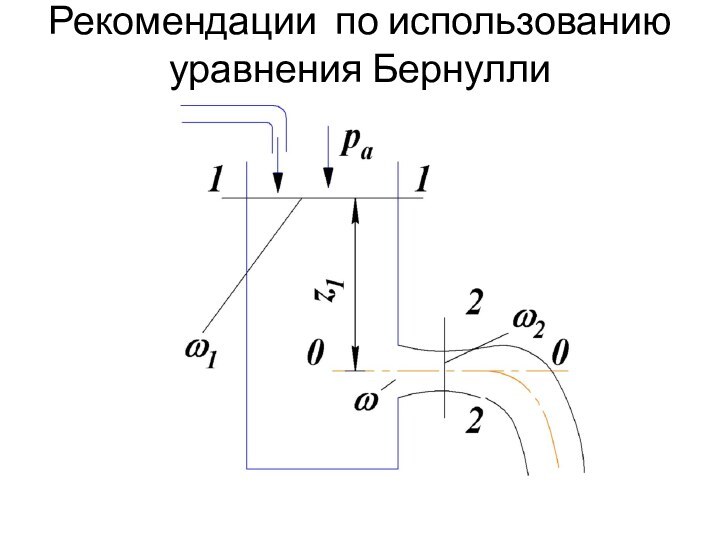
- 38. Рекомендации по использованию уравнения Бернулли
- 45. Скачать презентацию
- 46. Похожие презентации
Основные виды движения жидкостиУстановившееся движение жидкостиНеустановившееся движение жидкостиРазличают напорные и безнапорные течения жидкости





























Слайд 2
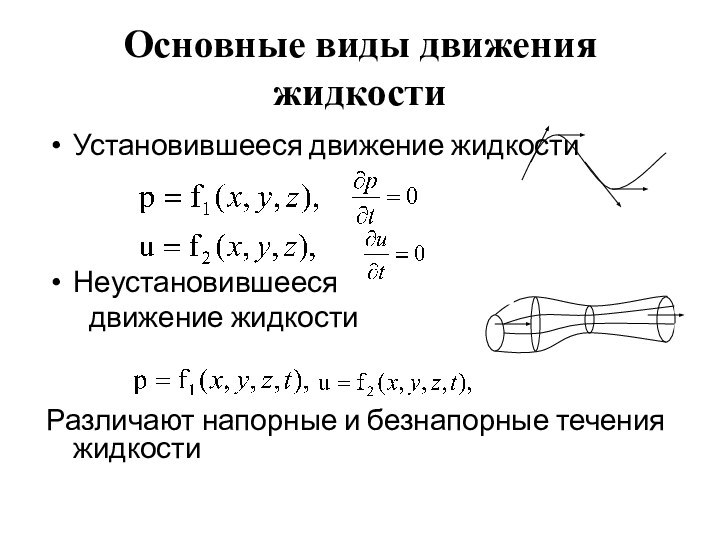
Основные виды движения жидкости
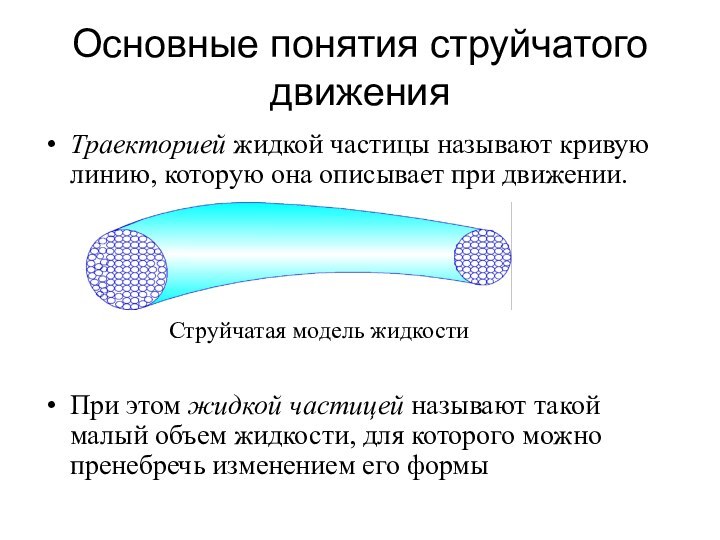
Установившееся движение жидкости
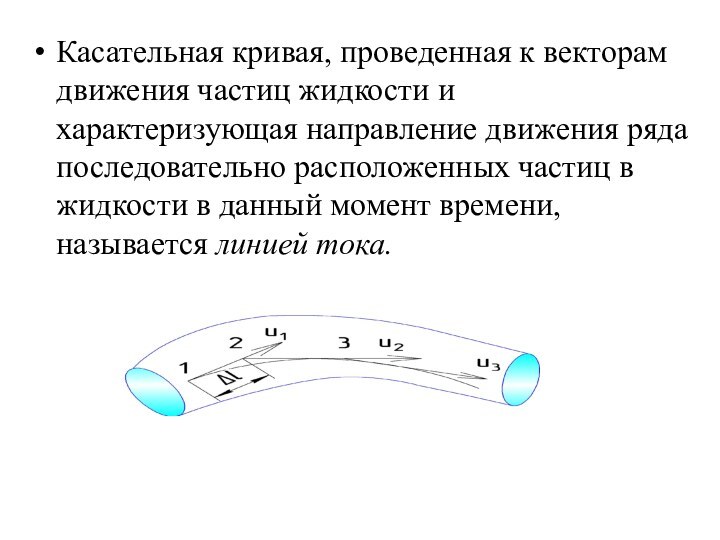
Неустановившееся
движение жидкости
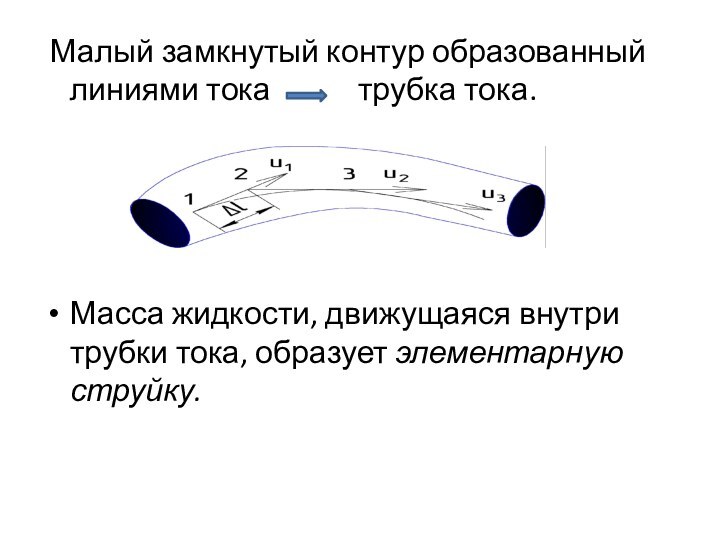
Различают
напорные и безнапорные течения жидкости
Слайд 3
Основные понятия струйчатого движения
Траекторией жидкой частицы называют кривую
линию, которую она описывает при движении.
Струйчатая модель жидкостиПри этом жидкой частицей называют такой малый объем жидкости, для которого можно пренебречь изменением его формы
Слайд 4 Касательная кривая, проведенная к векторам движения частиц жидкости
и характеризующая направление движения ряда последовательно расположенных частиц в
жидкости в данный момент времени, называется линией тока.Слайд 5 Малый замкнутый контур образованный линиями тока
трубка тока.
Масса жидкости, движущаяся
внутри трубки тока, образует элементарную струйку.Слайд 6 1) скорости и площади поперечных сечений струек в
одном живом сечении не меняются вследствие их малости;
2) скорости
и площади поперечных сечений струек в различных живых сечениях могут меняться, однако произведение скорости v отдельных частиц струйки на площади их поперечного сечения s остаются постоянными (уравнение неразрывности элементарной струйки).
Слайд 7
Методы изучения движения жидкости
В гидромеханике существуют два метода
изучения движения жидкости: метод Лагранжа и метод Эйлера.
1. Метод
Лагранжа заключается в изучении движения каждой отдельной частицы жидкости. Движение определяется положением частицы жидкости в функции от времени t. Движение частицы будет определено, если точно определить координаты x, y, и z в заданный момент времени t, что дает возможность построить траекторию движения частицы жидкости.Местная скорость
Слайд 8
Метод Эйлера
Метод Эйлера основан на изучении поля скоростей,
под которым понимается значение величины и скоростей во всех
точках пространства, занятого движущейся жидкостью.Переменными Эйлера являются значения скоростей Ux, Uy, Uz , которые определяются в зависимости от координат точек пространства и времени, т. е.
Слайд 9
Расход жидкости
Объем жидкости V, проходящей через живое сечение
трубопровода в единицу времени t, называют расходом Q= V/t.
Средняя скорость движения потока через сечение ω
Слайд 10
Уравнение неразрывности для элементарной струйки
Поток жидкости есть совокупность
элементарных струек. Эта масса непрерывная (неразрывна) и движется в
лювся в одном направленииu1·s1= s2·u2= si·ui=const
Слайд 11
Закон неразрывности потока
Схема потока
1S1v1= 2S2v2=iSivi=const
где v1, v2, vi
– скорости жидкости в сечениях 1, 2 и i;
S1, S2, Si – площади двух поперечных сечений трубопровода; 1, 2, i – плотности жидкости.
Слайд 14
Уравнения движения идеальной жидкости
Проекциями отнесенной к массе объема
жидкости силы инерции на оси х, у, z являются:
Система
дифуравнений Эйлера движенияидеальной жидкости
Слайд 16 В векторной форме вышезаписанные уравнения запишутся в следующем
виде:
Для несжимаемой невязкой жидкости (=const) данная система уравнений имеет
четыре неизвестных vx,vy,vz, p. Чтобы система стала замкнутой уравнение неразрывности
Слайд 17
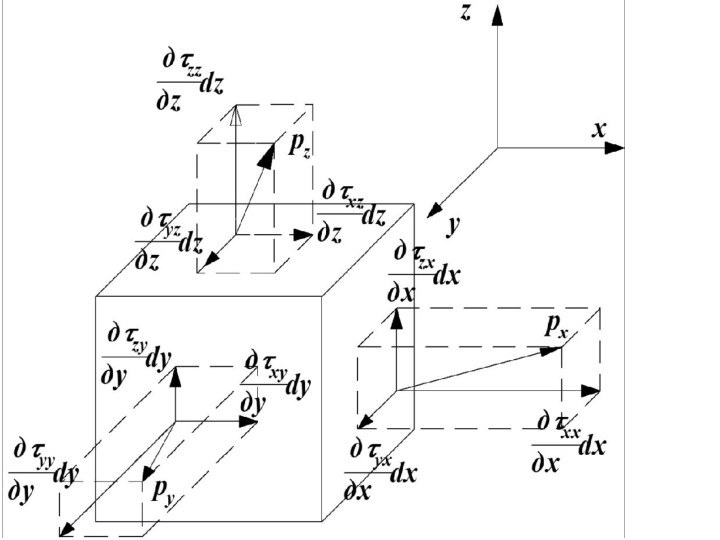
Уравнения Навье–Стокса
Проекции на ось x сил трения действующих
на прямоугольный параллелепипед дает следующее выражение:
Слайд 18 Используя закон Ньютона τ=μ·Δv/Δl , проекции сил
трения можно записать в компонентах скорости v на оси
x, y и z так:
Слайд 25
Полная удельная энергия потока
Определим слагаемые правой части:
кинетическая энергия
где
n – число элементарных струек;
u – скорости элементарных
струек. ЭУД= ЭК + ЭП,
Слайд 26
Коэффициент Кориолиса
– коэффициент Кориолиса, учитывающего неравномерность распределения
скорости по сечению
=1,0 – 1,13 – для турбулентных потоков
и =2,0 – для ламинарных потоков. Таким образом,
где v – средняя скорость потока;
Слайд 29
Уравнение Бернулли для реального потока жидкости
Здесь Δh
величина потерь энергии на преодоление сил трения между 1
и 2 участком
Слайд 30
Физический смысл уравнения
Физический (энергетический) смысл уравнения Бернулли
состоит в том, что при установившемся движении жидкости сумма
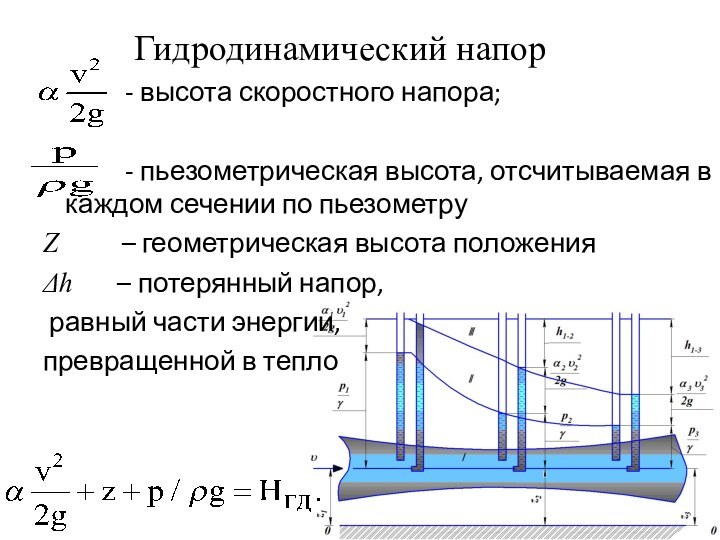
трех удельных энергий (положения, давления и кинетической) остается неизменной.Слайд 31 Гидродинамический
напор
- высота
скоростного напора;- пьезометрическая высота, отсчитываемая в каждом сечении по пьезометру
Z – геометрическая высота положения
Δh – потерянный напор,
равный части энергии,
превращенной в тепло
Слайд 35
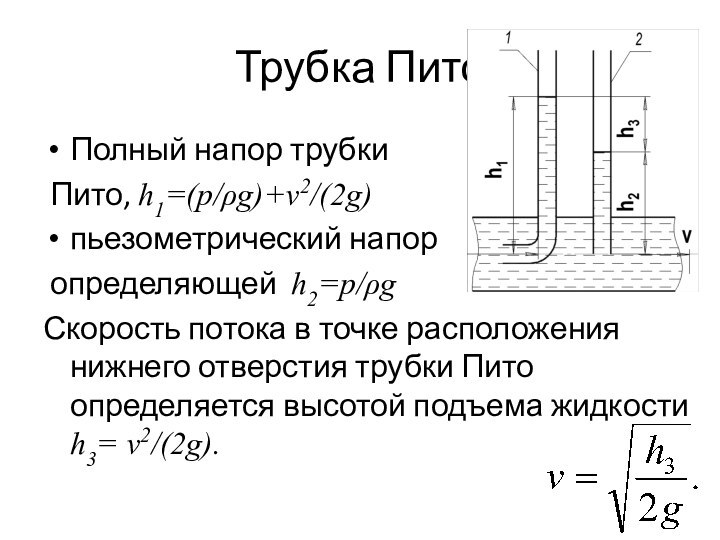
Трубка Пито
Полный напор трубки
Пито, h1=(p/g)+v2/(2g)
пьезометрический напор
определяющей h2=p/g
Скорость потока в точке расположения нижнего отверстия трубки
Пито определяется высотой подъема жидкости h3= v2/(2g).
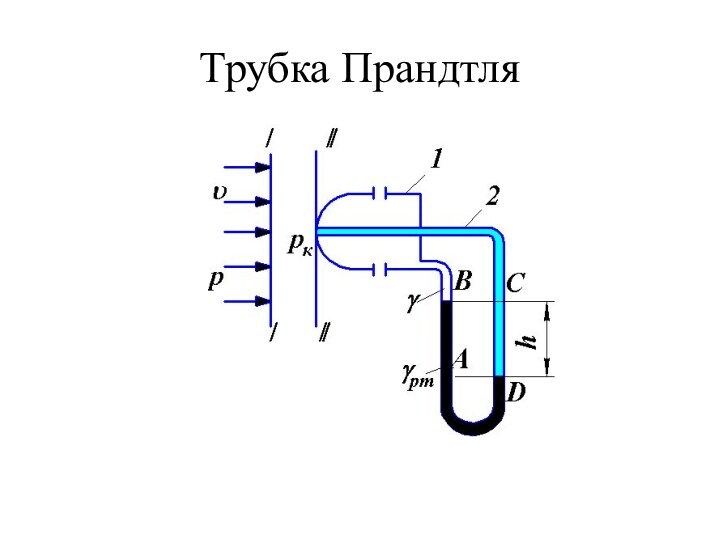
Слайд 36
Формула Торричелли
где – коэффициент расхода (истечения), который
определяется экспериментально и зависит от вида (формы) отверстия;
S
– площадь поперечного сечения отверстия; Δh=Δp/(g) – напор.





























