Слайд 2
Методы построения функции принадлежности
Измерения
Целью измерения является получение количественной
информации о величине исследуемых объектов, под которыми понимаются реально
существующие объекты (предметы, процессы, поля, явления и т.д.) материального мира, а также взаимодействия между ними.
Задачи измерения могут быть как познавательными (изучение элементарных частиц, организма человека и т.д.), так и прикладными (управление конкретным технологическим процессом, контроль качества продукции). Получение и использование информации — характерное свойство кибернетических систем. Поэтому измерение можно рассматривать как ту часть кибернетики, которая принимает в качестве объекта исследования предметы и явления окружающего мира, в качестве метода — эксперимент, а в качестве средства — измерительную технику.
Слайд 3
Методы построения функции принадлежности
Измерения
Серьезной составной частью большинства научно-исследовательских
работ являются измерения, позволяющие установить количественные соотношения и закономерности
изучаемых явлений.
"Надо измерять все измеримое и делать измеримым то, что пока не поддается измерению" (Галилео Галилей);
"Наука начинается с тех пор, как начинают измерять; точная наука немыслима без меры" (Д.И.Менделеев);
"Искусство измерения является могущественным орудием, созданным человеческим разумом для проникновения в законы природы" (Б.С.Якоби).
Прогресс в области измерений способствовал и способствует многим новым открытиям, а достижения науки, в свою очередь, — совершенствованию методов и средств измерений (например, благодаря использованию лазеров, микроэлектроники и т.п.).
Слайд 4
Методы построения функции принадлежности
Измерения
При проведении экспертиз важным условием
успеха является возможность формализовать информацию, не поддающуюся количественному измерению,
так, чтобы помочь принимающему решение выбрать из множества действий одно.
Поэтому в вопросах, связанных с теорией измерений, основное место отводится понятию шкалы измерения.
В зависимости от того, по какой шкале идет измерение, экспертные оценки содержат больший или меньший объем информации и обладают различной способностью к математической формализации.
Слайд 5
Шкалы и размерности - виды
Измерение - процесс присвоения
чисел характеристикам изучаемых объектов согласно определенному правилу.
Шкала - правило,
в соответствии с которым объектам присваиваются числа.
Пять типов шкал измерений:
номинальная,
порядковая,
интервальная,
относительная
дихотомическая.
Относительные и интервальные шкалы являются числовыми.
Слайд 6
Номинальная шкала
Номинальная шкала - шкала, содержащая только категории;
данные в ней не могут упорядочиваться, с ними не
могут быть произведены никакие арифметические действия
Пример шкалы: профессии, город проживания, семейное положение.
Применимы только операции: равно (=), не равно ().
Слайд 7
Порядковая шкала
Порядковая шкала (ordinal scale) - шкала, в
которой числа присваивают объектам для обозначения относительной позиции объектов,
но не величины различий между ними.
Измерения в порядковой шкале содержат информацию только о порядке следования величин, но не позволяют сказать "насколько одна величина больше другой", или "насколько она меньше другой".
Пример такой шкалы: номер студента в рейтинге успеваемости (1-й, 23-й, и т.д.), при этом неизвестно, насколько один студент успешней другого, известен лишь его номер в рейтинге.
Применимы только операции: равно (=), не равно (), больше (>), меньше (<).
Слайд 8
Интервальная шкала
Интервальная шкала (interval scale) - шкала, разности
между значениями которой могут быть вычислены, однако их отношения
не имеют смысла.
Эта шкала позволяет находить разницу между двумя величинами, обладает свойствами номинальной и порядковой шкал, а также позволяет определить количественное изменение признака.
Пример шкалы: возраст от 35 до 39 лет, от 40 до 45. Нельзя сказать, что второй диапазон во столько-то раз выше.
Применимы операции: равно (=), не равно (), больше (>), меньше (<), операции сложения (+) и вычитания (-).
Слайд 9
Относительная шкала
Относительная шкала - шкала, в которой есть
определенная точка отсчета и возможны отношения между значениями шкалы.
Пример
шкалы: цена на картофель в супермаркете выше в 1,2 раза, чем цена на рынке.
Для этой шкалы применимы операции: равно (=), не равно (), больше (>), меньше (<), операции сложения (+) и вычитания (-), умножения (*) и деления (/).
Слайд 10
Дихотомическая шкала
Дихотомическая шкала - шкала, содержащая только две
категории.
Пример такой шкалы: пол (мужской и женский).
Слайд 11
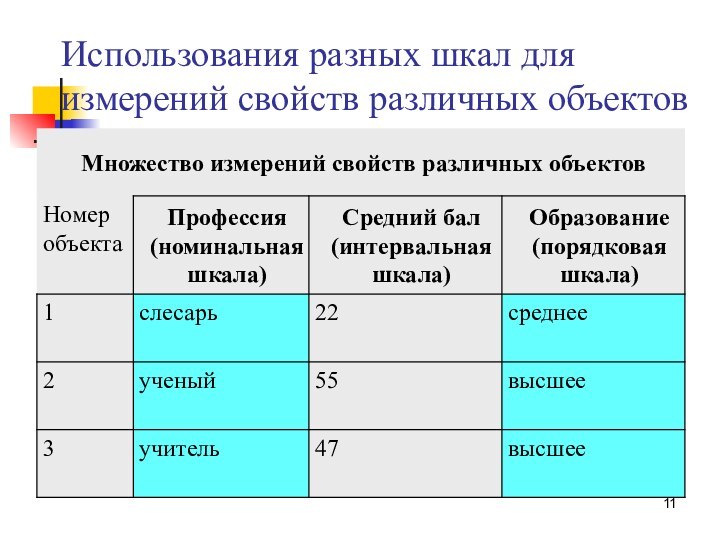
Использования разных шкал для измерений свойств различных объектов
Слайд 12
Методы измерений
Ранжирование. При ранжировании эксперт располагает объекты в
порядке предпочтения, руководствуясь одним или несколькими показателями сравнения.
Парная
оценка или метод парных сравнений представляет собой процедуру установления предпочтений объектов при сравнении всех возможных пар.
Непосредственная оценка представляет собой процедуру приписывания объектам числовых значений по шкале интервалов. Эквивалентным объектам приписывается одно и то же число. Этот метод может быть осуществлен только при полной информированности экспертов о свойствах объектов. Вместо числовой оси может использоваться балльная оценка.
Последовательное сравнение включает в себя ранжирование и непосредственную оценку.
Слайд 13
Методы проведения групповой экспертизы
очные и заочные;
индивидуальные и коллективные;
с
обратной связью и без обратной связи.
При очном методе проведения
экспертизы эксперт работает в присутствии организатора исследования.
При коллективном методе проведения экспертизы поставленная проблема решается сообща, "за круглым столом".
При индивидуальном — каждый эксперт оценивает проблему, исходя из личного опыта и убеждений.
Экспертиза с обратной связью (метод Дельфы) предусматривает проведение нескольких туров опроса и анонимное анкетирование. После каждого тура экспертные оценки обрабатываются, и результаты обработки сообщаются экспертам.
Метод без обратной связи предусматривает один тур опроса при получении удовлетворительных результатов.
Слайд 14
Особенности методов построения функции принадлежности
Для теории нечетких множеств
основополагающим понятием является понятие нечеткого множества, которое характеризуется функцией
принадлежности. Посредством нечеткого множества можно строго описывать присущие языку человека расплывчатые элементы, без формализации которых нет надежды существенно продвинуться вперед в моделировании интеллектуальных процессов.
Но основной трудностью, мешающей интенсивному применению теории нечетких множеств при решении практических задач, является то, что функция принадлежности должна быть задана вне самой теории и, следовательно, ее адекватность не может быть проверена средствами теории.
В каждом существующем в настоящее время методе построения функции принадлежности формулируются свои требования и обоснования к выбору именно такого построения.
Слайд 15
Особенности методов построения функции принадлежности
Слайд 16
Методы построения функции принадлежности
Прямые методы
Слайд 17
Методы построения функции принадлежности Косвенные методы
Слайд 18
Прямые методы для одного эксперта
Прямые методы для одного
эксперта состоят в непосредственном задании функции, позволяющей вычислять значения.
Используются,
как правило, для измеримых понятий, таких как скорость, время, давление, температура и т.д.
Слайд 19
Построение функции принадлежности на непрерывном множестве точек
Выбор вида
функции принадлежности и их параметров определяется в большей степени
опытом, интуицией и другими субъективными факторами лица, принимающего решение. В следующей таблице приведены некоторые простейшие функции принадлежности, которые можно предложить эксперту.
Слайд 20
Типовые формы кривых
1. Треугольная (trimf)
Слайд 21
Типовые формы кривых
2. Трапециевидная (trapmf)
Слайд 22
Типовые формы кривых
3. Гаусса (gaussmf, gauss2mf)
Слайд 23
Типовые формы кривых
4. «Обобщенный колокол» (gbellmf)
Слайд 24
Типовые формы кривых
5. Сигмоидные (sigmf, dsigmf, psigmf)
Слайд 25
Типовые формы кривых
6. Z- функция (zmf)
Слайд 26
Типовые формы кривых
7. S-функция (smf)
Слайд 27
Построение функции принадлежности на непрерывном множестве точек
Слайд 28
Построение функции принадлежности на непрерывном множестве точек
Слайд 29
Построение функции принадлежности на непрерывном множестве точек
Слайд 30
Построение функции принадлежности на непрерывном множестве точек
Слайд 31
Метод семантических дифференциалов
(предложен Осгудом)
Практически в любой области
можно получить множество шкал оценок, используя следующую процедуру:
1. определить
список свойств, по которым оценивается понятие (объект);
2. найти в этом списке полярные свойства и сформировать полярную шкалу;
3. для каждой пары полюсов оценить, в какой степени введенное понятие обладает положительным свойством.
Совокупность оценок по шкалам была названа профилем понятия. Следовательно, вектор с координатами, изменяющимися от 0 до 1, также называется профилем. Профиль есть нечеткое подмножество положительного списка свойств или шкал.
Слайд 32
Многомерная функция принадлежности
Слайд 33
Пример. В задаче распознавания лиц можно выделить следующие
шкалы:
Задайте каждый для себя свою функцию принадлежности.
Слайд 34
Пример. Способ вычисления частичной принадлежности друг другу строгих
множеств.
Слайд 36
Пример. Решение задачи многоцелевой оптимизации
Слайд 37
Построение функций принадлежности на счетном множестве на основе
экспертных оценок (групповые прямые методы)
Слайд 38
Косвенные методы для одного эксперта
В обыденной жизни мы
часто сталкиваемся со случаями, когда не существует элементарных измеримых
свойств и признаков, которые определяют интересующие нас понятия, например, красоту, интеллектуальность. Бывает трудно проранжировать степень проявления свойства у рассматриваемых элементов. Так как степени принадлежности рассматриваются на данном реальном множестве, а не в абсолютном смысле, то интенсивность принадлежности можно определять, исходя из попарных сравнений рассматриваемых элементов.
Среди косвенных методов определения функции принадлежности наибольшее распространение получил метод парных сравнений.
Слайд 39
Косвенные методы построения функции принадлежности на счетном множестве
на основе количественного парного сравнения степеней принадлежности
Результатом опроса эксперта
является матрица М = || mij ||, i, j = 1, …, n, где n – число точек, в которых сравниваются значения функции принадлежности. Число mij показывает, во сколько раз, по мнению эксперта, степень принадлежности µА(хi) больше µА(хj).
При этом эксперт оперирует понятиями, представленными в таблице
(9 балльная шкала Саати).
Слайд 40
Косвенные методы построения функции принадлежности на счетном множестве
на основе количественного парного сравнения степеней принадлежности
Слайд 42
Косвенные методы построения функции принадлежности на счетном множестве
на основе количественного парного сравнения степеней принадлежности
Далее, определить значение
функции принадлежности µА в точках х1, х2, …, хn можно, используя формулу:
где j – произвольный столбец матрицы М.
Слайд 43
Косвенные методы для группы экспертов. Определение функции принадлежности
на основе интервальных оценок (метод Шера)
Слайд 44
Косвенные методы для группы экспертов. Определение функции принадлежности
на основе интервальных оценок (метод Шера)