экспериментальных средств;
Проведение эксперимента, в котором по возможности наиболее полно
отображаются реальные условия взаимодействия объекта исследования с окружающей средой.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Повторные эксперименты Массив данных Систематизация и статистическая обработка
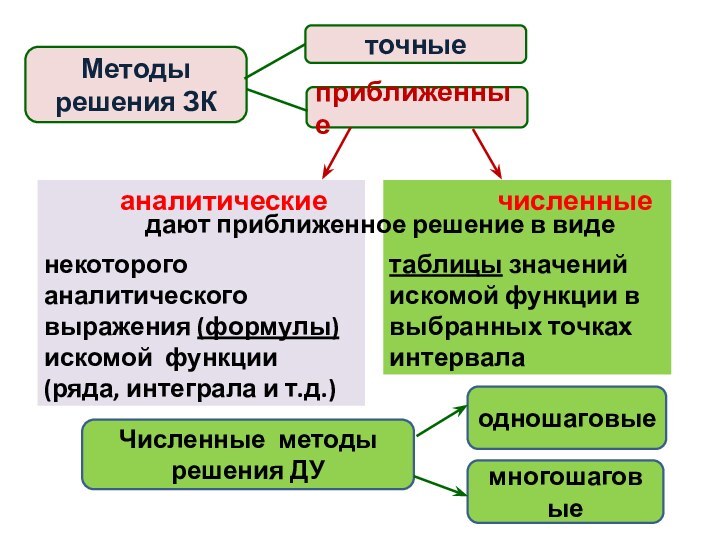
Изображение в виде
таблиц,
графиков,
эксперимент. функциональных зависимостей.







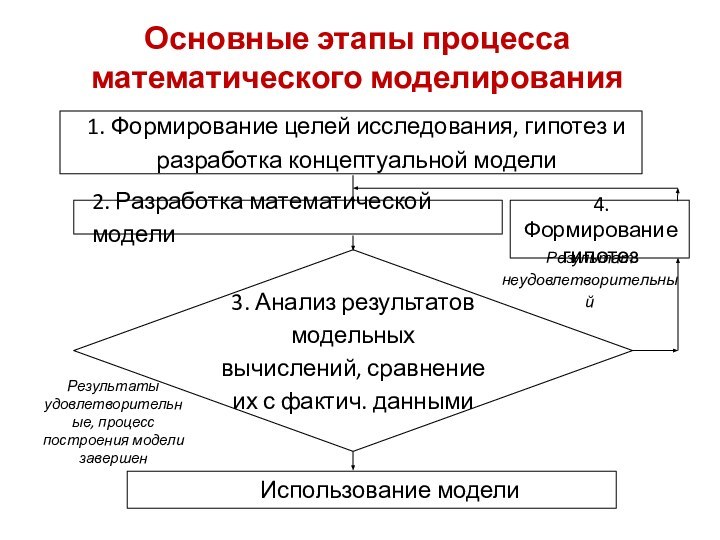






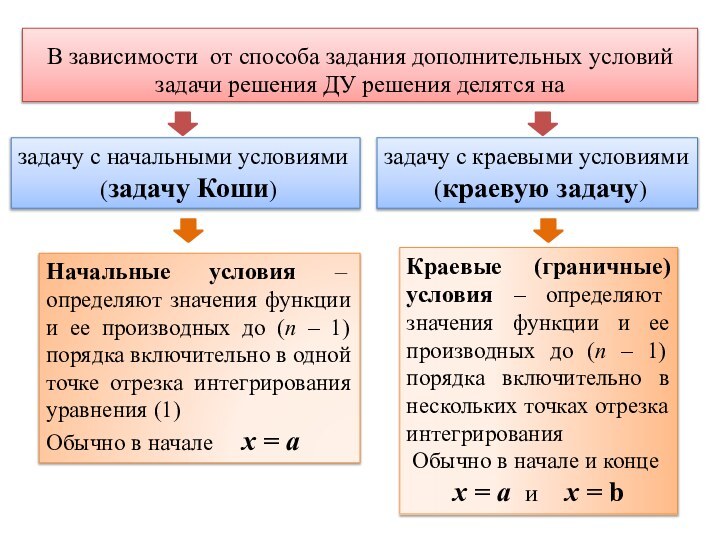






![ММИР YXhy = y(x)y ʹ = f(x , y) , x [a, b]](/img/tmb/14/1390067/39ea8f90d35b2cb0723815d32a4073e7-720x.jpg)








![ММИР Введем в рассмотрение дифференциальный оператор Ly и функционал lν [y], тогда (1)](/img/tmb/14/1390067/9ce7f2fa40cec9f12d1d7156f709e2ae-720x.jpg)

![ММИР Разобьем [a, b] на n равных частей длиной h =](/img/tmb/14/1390067/b90daf826c105887967a77f45159fe32-720x.jpg)