- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Нечёткая логика
Содержание
- 2. Нечёткая логика Нечёткая логика— раздел математики, являющийся
- 3. Предметом нечёткой логики считается исследование рассуждений в
- 4. Примером нечёткой логики может являться,определения лингвистической переменной
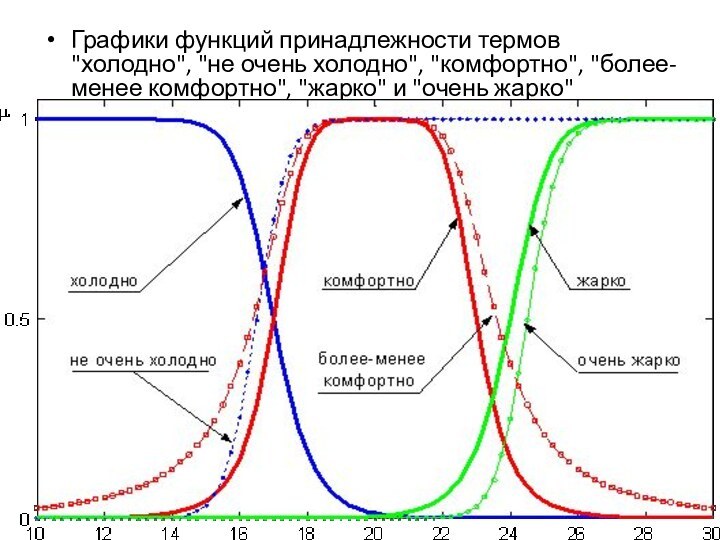
- 5. Графики функций принадлежности термов "холодно", "не очень
- 6. Характеристические функции:
- 7. Правило G порождает новые термы с использованием
- 8. ОпределениеПод нечётким множеством A понимается совокупность упорядоченных пар, составленных
- 9. Скачать презентацию
- 10. Похожие презентации
Нечёткая логика Нечёткая логика— раздел математики, являющийся обобщением классической логики и ткории множеств, базирующийся на понятии нечёткого множества, принимающей любые значения в интервале [0,1], а не только 0 или 1. На основе этого понятия вводятся различные логические операции над нечёткими множествами








Слайд 2
Нечёткая логика
Нечёткая логика— раздел математики, являющийся обобщением классической логики
Слайд 3 Предметом нечёткой логики считается исследование рассуждений в условиях
нечёткости, размытости, сходных с рассуждениями в обычном смысле, и
их применение в вычислительных системах.
Слайд 4
Примером нечёткой логики может являться,определения лингвистической переменной
В
обозначениях, принятых для лингвистической переменной:
X = «Температура в комнате»
U =
[5, 35]T = {«холодно», «тепло», «жарко»}
Слайд 5 Графики функций принадлежности термов "холодно", "не очень холодно",
"комфортно", "более-менее комфортно", "жарко" и "очень жарко" лингвистической переменной
"температура в комнате"Слайд 7 Правило G порождает новые термы с использованием союзов
«и», «или», «не», «очень», «более или менее».
Слайд 8
Определение
Под нечётким множеством A понимается совокупность упорядоченных пар, составленных из
элементов xуниверсального множества X и соответствующих степеней принадлежности μA(x)
A={(x,μA(x))|x∈X}причем μA(x) —характеристическая функция, указывающая в какой степени (мере) элемент x принадлежит нечёткому множеству A.





























