Презентация на тему Обобщение 2 главы

треугольника
Параграф 3.Второй и третий признаки равенства треугольников
Параграф 4.Задачи на

построение
Используемые материалы

лежащие на одной прямой , и соединённые отрезками ,

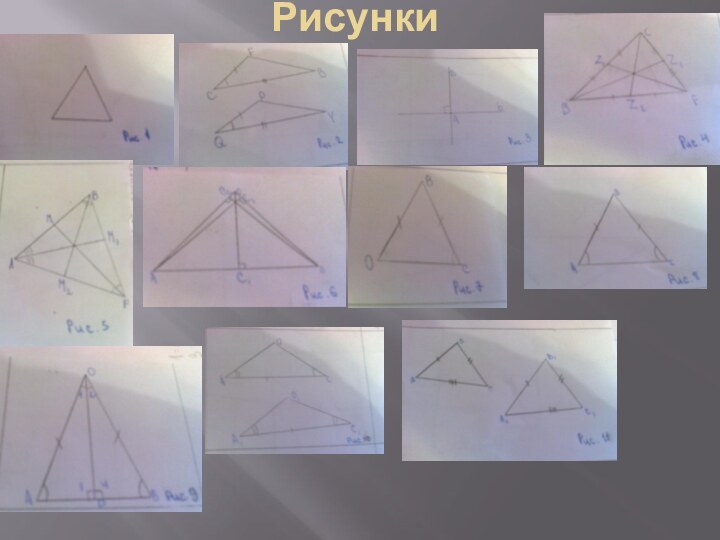
называются треугольником.Отмеченные три точки называются вершинами,а отрезки – сторонами треугольника.(см. рис.1)

2)Сумма длин трёх сторон треугольника называется его периметром.
3)Две фигуры , в частности два треугольника , называются равными , если их можно совместить наложением.
4)Если два треугольника равны , то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
5)В равных треугольниках против соответственно равных сторон(т.е. совмещающихся при наложении) лежат равные углы , и обратно : против соответственно равных углов лежат равные стороны.

путём рассуждений , называется теоремой ,а сами рассуждения называются

доказательством теоремы.
2) Теорема
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника , то такие треугольники равны.(смю рис. 2)

3)Доказанная теорема выражает признак( равенство у треугольников двух сторон и угла между ними) , по которому можно сделать вывод о равенстве треугольников.Он называется первым признаком равенства треугольников.

Из точки , не лежащей на прямой , можно

провести перпендикуляр к этой прямой , и притом только один.(см. рис. 3)
2)Для проведения на чертеже перпендикуляра из точки к прямой используют чертёжный угольник.

, называется медианой треугольника .Любой треугольник имеет три медианы.В

любом треугольнике медианы пересекаются в одной точке.(см. рис. 4)


2)Отрезок биссектрисы угла треугольника,
соединяющий вершину треугольника с точкой противоположной стороны , называется биссектрисой треугольника.Любой треугольник имеет три биссектрисы.Биссектрисы в любом треугольнике пересекаются в одной точке.(см. рис.5)

3)Перпендикуляр,проведённый из вершины треугольника к прямой , содержащей противоположную сторону , называется высотой треугольника.(см. рис.6)

стороны называются боковыми сторонами,в третья сторона – основанием равнобедренного

треугольника.(см. рис.7)
2)Треугольник , все стороны которого равны , называется равносторонним.
3)Теорема
В равнобедренном треугольнике углы при основании равны.(см. рис.8)

4)Теорема
В равнобедренном треугольнике биссектриса , проведённая к основанию , является медианой и высотой.(см. рис. 9)

5) Высота равнобедренного треугольника , проведённая к основанию является медианой и биссектрисой.
Медиана равнобедренного треугольника , проведённая к основанию,является высотой и биссектрисой.(см. рис.9)

Если сторона и два прилежащих к ней угла одного

треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника , то такие треугольники равны.(см. рис. 9)

равны трём сторонам другого треугольника , то такие треугольники

равны.(см. рис.10)
2)Из третьего признака равенства треугольников следует,что треугольник – жёсткая фигура.

или иного выражения или названия,называется определением.
2)Определение
Окружностью называется

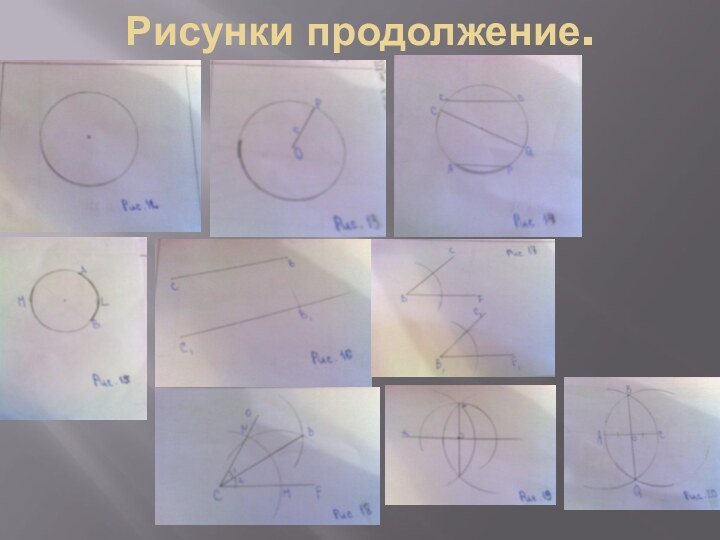
геометрическая фигура,состоящая из всех точек плоскости , расположенных на заданном расстоянии от данной точки.(см. рис.11)
3)Данная точка называется центром окружности , а отрезок,соединяющий центр с какой-либо точкой окружности, - радиусом окружности(см. рис. 12)

4)Отрезок,соединяющий две точки окружности , называется её хордой.Хорда,проходящая через центр окружности , называется диаметром.(см. рис. 13)

5)Любые две точки окружности делят её на две части.Каждая из этих частей называется дугой окружности.(см. рис.14)

, а также построить прямую , проходящую через две

данные точки.С помощью циркуля можно провести окружность произвольного радиуса , а также окружность с центром в данной точке и радиусом , равным данному отрезку. Выполняя эти несложные операции , мы сможем решить много интересных задач на построение.

рис. 16)




3)Построение биссектрисы угла(см. рис.17)





4)Построение перпендикулярных прямых(см. рис. 18)
5)Построение

середины отрезка(см. рис.19)

Учебник по геометрии 7-9 класс,издательство «Просвещение»,авторы:Л.С. Атанасян,В.Ф. Бутузов,С.Б. Кадомцев,Э.Г. Позняк,И.И. Юдина