Слайд 2
Доказательство и опровержение
Понятие, структура и правила доказательства
Определение
доказательства
Структура доказательства
Тезис
Доводы (аргументы)
Демонстрация
Виды доказательства
Прямое и косвенное доказательства
Индуктивное и
дедуктивное доказательства
Понятие и способы опровержения
Определение опровержения
Основные приёмы опровержения
Слайд 3
Понятие доказательства
Определение доказательства
Доказательство –
логическое действие,
в процессе которого
истинность
какой-либо мысли
обосновывается
с помощью других мыслей,
истинность которых уже установлена.
Доказательство представляет
собой
разновидность логического вывода,
особенностью которой является то, что
процедура умозаключения используется
в данном случае не для получения нового,
а для обоснования истинности
уже имеющегося знания.
Слайд 4
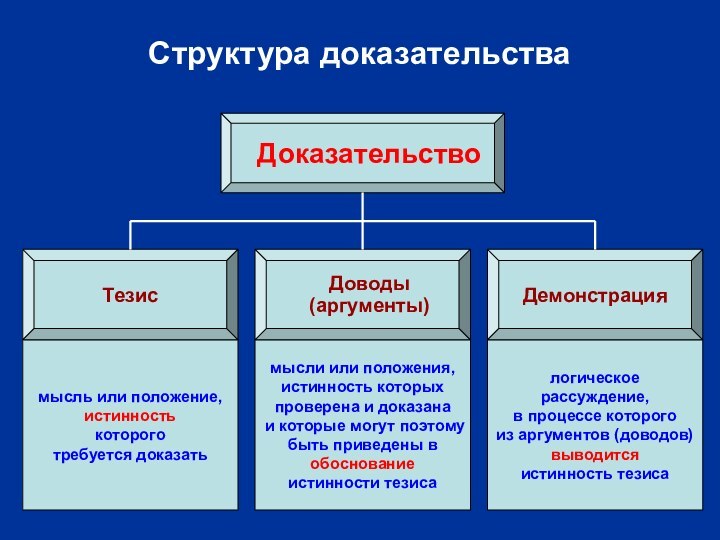
Структура доказательства
Доказательство
Тезис
Доводы
(аргументы)
Демонстрация
мысль или положение,
истинность
которого
требуется доказать
мысли или положения,
истинность которых
проверена
и доказана
и которые могут поэтому
быть приведены в
обоснование
истинности тезиса
логическое рассуждение,
в
процессе которого
из аргументов (доводов)
выводится
истинность тезиса
Слайд 5
Структура доказательства
Тезис
Основное требование к тезису:
Тезис должен быть
истинным суждением. Если тезис ложен, то никакое доказательство не
сумеет его обосновать.
Это не значит, что ложное суждение не может быть получено путём логического вывода (ложный вывод без труда получается, например, из ложных посылок), но цена такому «выводу» – грош.
Правила тезиса:
Тезис должен быть суждением ясным и точно определённым.
Тезис должен оставаться тождественным, т. е. одним и тем же на протяжении всего доказательства.
Тезис не должен быть логически противоречив.
Тезис не должен противоречить другим суждениям по данному вопросу.
Тезис должен быть обоснован фактами.
Тезисом не должно быть суждение очевидное, так как то, что достоверно само по себе, не требует доказательства.
Тезис должен определять собою весь ход доказательства – с тем, чтобы в итоге было доказано именно то, что требовалось доказать.
Слайд 6
Структура доказательства
Довод
Основное требование к доводу:
Довод должен быть
доказанным истинным суждением.
Наиболее характерные ошибки:
«Основное заблуждение»
«Предвосхищение основания»
Логические операции
с доводами подчиняются следующим правилам:
Доводы должны являться достаточным основанием тезиса.
Наиболее характерные ошибки:
«Не следует» («не вытекает»)
«От сказанного в относительном смысле к сказанному безотносительно»
«Кто доказывает слишком много, не доказывает ничего»
Истинность довода должна быть обоснована независимо от тезиса.
Наиболее характерная ошибка:
«Порочный круг»
Доводы, приводимые в подтверждение тезиса, не должны противоречить друг другу.
Слайд 7
Правило первое: довод должен быть
доказанным истинным суждением
«Основное заблуждение»
(лат.
error fundamentalis) –
логическая ошибка,
вызванная
нарушением закона
достаточного основания
в процессе аргументации,
когда тезис
обосновывается
ложными
аргументами.
«Доказательства»,
основанные на ложных аргументах,
не имеют логической силы.
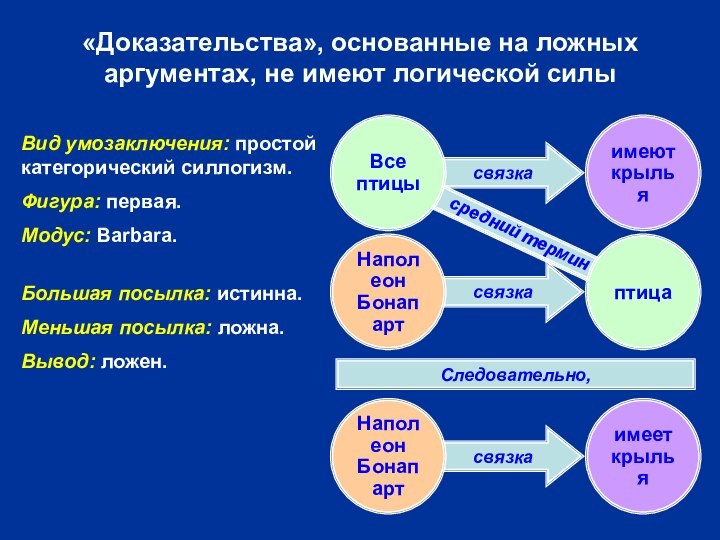
Слайд 8
связка
связка
связка
связка
«Доказательства», основанные на ложных аргументах, не имеют логической
силы
Наполеон
Бонапарт
имеет
крылья
Следовательно,
средний термин
Все
птицы
имеют
крылья
Наполеон
Бонапарт
птица
Вид умозаключения: простой категорический силлогизм.
Фигура: первая.
Модус: Barbara.
Большая
посылка: истинна.
Меньшая посылка: ложна.
Вывод: ложен.
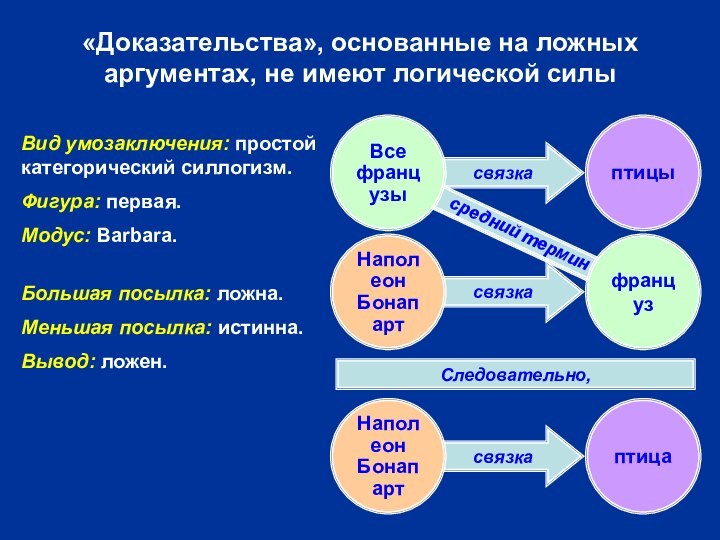
Слайд 9
связка
связка
связка
связка
«Доказательства», основанные на ложных аргументах, не имеют логической
силы
Наполеон
Бонапарт
птица
Следовательно,
средний термин
Все
французы
птицы
Наполеон
Бонапарт
француз
Вид умозаключения: простой категорический силлогизм.
Фигура: первая.
Модус: Barbara.
Большая
посылка: ложна.
Меньшая посылка: истинна.
Вывод: ложен.
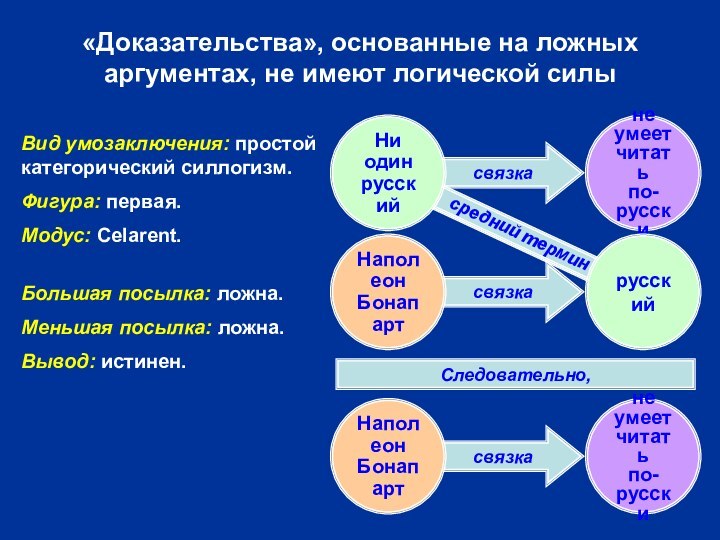
Слайд 10
связка
связка
связка
связка
«Доказательства», основанные на ложных аргументах, не имеют логической
силы
Наполеон
Бонапарт
не умеет
читать
по-русски
Следовательно,
средний термин
Ни один
русский
не умеет
читать
по-русски
Наполеон
Бонапарт
русский
Вид умозаключения: простой категорический
силлогизм.
Фигура: первая.
Модус: Celarent.
Большая посылка: ложна.
Меньшая посылка: ложна.
Вывод: истинен.
Слайд 11
«Доказательства», основанные на ложных аргументах, не имеют логической
силы
Если дважды два – пять, то я – папа римский.
Запишем
«дважды два» в виде суммы: 2 + 2.
Получим, что 2 + 2 = 5.
Вычтем из обеих частей по двойке – получим: 2 = 3.
Переставим правую и левую части – получим: 3 = 2.
Вычтем из обеих частей по 1 – получим: 2 = 1.
Нас с папой римским – двое.
Но так как 2 = 1, то папа римский и я – одно лицо.
Следовательно, я – папа римский.
Б. Рассел
Строго говоря,
из ложного утверждения
вообще «следует» что угодно.
Слайд 12
Правило первое: довод должен быть
доказанным истинным суждением
«Предвосхищение основания»
(лат.
petitio principii) –
логическая ошибка,
связанная
с нарушением закона
достаточного основания
в процессе аргументации:
в
качестве основания (аргумента),
подтверждающего тезис,
приводится такое положение,
которое, хотя и не является
заведомо ложным,
само нуждается в доказательстве.
Ничего нельзя доказать
с помощью положений,
истинность которых не установлена.
Слайд 13
Ничего нельзя доказать с помощью положений, истинность которых

не установлена
Может, вы и не заметили, но плохие парни
сегодня живут припеваючи,
при условии, что они богаты нефтью. Купающийся в нефтедолларах Иран
показывает язык в ответ на все требования ООН о прекращении ядерной
авантюры и ежедневно грозится стереть Израиль с лица земли.
Купающийся в нефтедолларах президент России Владимир Путин сажает
своих оппонентов в тюрьмы и подлизывается к оппонентам Америки,
таким, как Иран и ХАМАС. Купающийся в нефтедолларах Судан игнорирует
мольбы мирового сообщества о прекращении геноцида в Дарфуре.
Купающийся в нефтедолларах президент Венесуэлы Уго Чавес регулярно
посылает ко всем чертям своих политических противников и Америку.
А Нигерия, Узбекистан, Ангола, Саудовская Аравия, Чад и Сирия –
богатые кто нефтью, кто газом, – спокойно отказываются даже
от тех крошечных шажков к демократизации, которые были сделаны.
Здесь прослеживается определенная закономерность...
Я называю это Первым законом петрополитики, и звучит он так:
уровень цен на нефть и уровень свободы в нефтегосударствах
неизменно связаны обратно пропорциональной зависимостью.
Томас Л. Фридман
Слайд 14
Правило второе: доводы должны являться
достаточным основанием тезиса
«Не
следует» («не вытекает»)
(лат. non sequetur) –
логическая ошибка,
вызванная
нарушением закона
достаточного основания
в
процессе аргументации:
в подтверждение тезиса
выставляются доводы,
сами по себе верные,
но не являющиеся
достаточным основанием
для тезиса и потому
не доказывающие его.
Не может служить доказательством
положение, из которого
доказываемый тезис не следует.
Слайд 15
Не может служить доказательством положение, из которого доказываемый
тезис не следует
Предположим, кто-то взялся доказать шарообразность Земли с
помощью следующих наглядных доводов:
При приближении корабля к берегу сперва показываются из-за горизонта верхушки мачт, а потом уже его корпус.
После захода солнца его лучи продолжают освещать крыши высоких зданий, вершины гор и облака, позднее – только вершины гор и облака, ещё позднее – только облака.
Но из этих «доводов» совершенно не следует, что Земля шарообразна:
они доказывают только кривизну земной поверхности,
замкнутость её формы
и изолированность Земли в пространстве.
Истинность тезиса о шарообразности Земли доказывается другими доводами, а именно:
В любом месте Земли горизонт представляется окружностью, и дальность горизонта всюду одинакова.
Во время лунного затмения тень Земли, падающая на Луну, всегда имеет круглые очертания, а круглую тень при любом положении отбрасывает только шар.
Слайд 16
Правило второе: доводы должны являться
достаточным основанием тезиса
«От
сказанного
в относительном смысле к
сказанному безотносительно»
(лат. a dicto secundum
quid
ad dictum simpliciter) –
логическая ошибка,
связанная
с нарушением закона
достаточного основания
в процессе аргументации:
положение, верное при
определённых условиях,
приводится в качестве аргумента,
годного при всех условиях.
«Доказательство», основанное
на поспешном обобщении,
не имеет логической силы.
Слайд 17
«Доказательство», основанное на поспешном обобщении, не имеет логической

силы
Выглянув утром в окно и увидев, что мостовая –
мокрая, не спешите делать вывод о том, что ночью прошёл дождь.
Разумеется, если бы ночью прошёл дождь, мостовая к утру была бы мокрой, но тот же результат имел бы место и после прохождения поливальной машины.
Вот если бы выглянув утром в окно, вы увидели, что мостовая – сухая, вы вполне могли бы заключить, что ночью дождя не было (как не проходила и поливальная машина, а если и проходила, то мостовую не поливала).
Умозаключение от мокрой мостовой к ночному дождю нарушает закон достаточного основания: это дождь является достаточным (хотя и не необходимым) условием мокрой мостовой, тогда как мокрая мостовая, хотя и является необходимым основанием для вывода о прошедшем дожде, была бы достаточным основанием для такого вывода лишь при дополнительном (в данном случае – не выполненном) условии, а именно: если бы дождь был единственной возможной причиной наличия воды на мостовой.
Слайд 18
Правило второе: доводы должны являться
достаточным основанием тезиса
«Кто
чрезмерно доказывает,
тот ничего не доказывает»
(лат. qui nimium probat,
nihil
probat) –
логическая ошибка
в доказательстве:
из предложенных оснований
следует не только
доказываемый тезис,
но и какое-нибудь
прямо противоположное
или ложное положение.
Тезис не может быть доказан
посредством того, что можно
использовать для его опровержения.
Слайд 19
Тезис не может быть доказан посредством того,
что
можно использовать для его опровержения
В качестве обоснования справедливости войны,
которую мы ведём, нельзя приводить доблесть наших солдат, потому что:
в таком случае доблесть неприятельских солдат надо будет признать доказательством справедливости войны со стороны неприятеля,
в результате чего мы придём к нелепому выводу, что обе воюющие стороны ведут справедливую войну;
тогда как отсутствие доблести со стороны отдельных наших солдат (а такое всегда имеет место) придётся считать доказательством несправедливости войны с нашей стороны,
которая таким образом окажется одновременно справедливой и несправедливой.
Слайд 20
Правило третье: истинность довода должна быть обоснована независимо
от тезиса
«Порочный круг»
(лат. circulus vitiosus) –
логическая ошибка,
вызванная
нарушением закона
достаточного
основания
в процессе аргументации:
тезис выводится из аргументов,
которые, в свою очередь,
выводятся из того же тезиса.
Не может служить доказательством
положение, истинное лишь при условии
истинности того, что следует доказать.
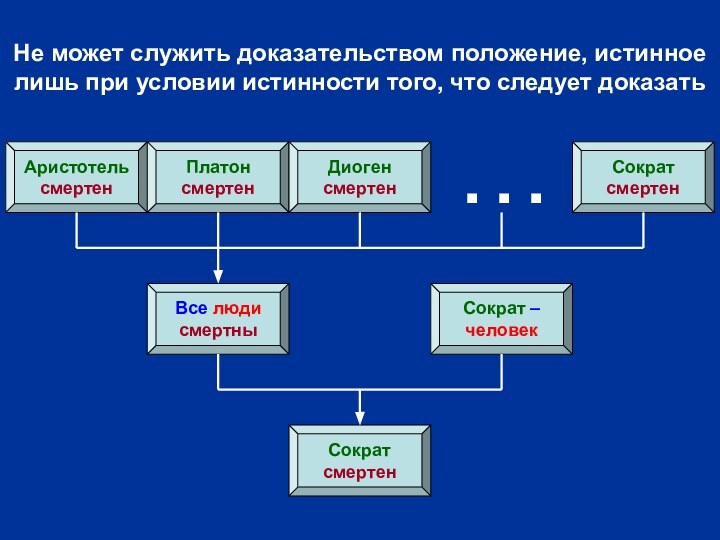
Слайд 21
Не может служить доказательством положение, истинное лишь при
условии истинности того, что следует доказать
Сократ
смертен
Все люди
смертны
Сократ –
человек
Аристотель
смертен
Платон
смертен
Диоген
смертен
Сократ
смертен
…
Слайд 22
Правило четвёртое: доводы, приводимые в подтверждение тезиса, не
должны противоречить друг другу
В жизни нет ничего,
кроме одиночества,
невзгод и страданий,
и – в довершение ко всему –
она слишком быстро
приходит к концу.
Вуди Аллен
Слайд 23
Структура доказательства
Демонстрация
Демонстрация
(лат. demonstratio) –
логическое рассуждение,
в процессе которого
из
аргументов (доводов)
выводится
истинность или ложность тезиса.
Под демонстрацией
понимается также
совокупность логических правил,
используемых
в доказательстве.
Слайд 24
Демонстрация
Правила доказательства
Тезис и аргументы должны быть истинными суждениями.
Тезис
и аргументы должны быть суждениями ясными и точно определёнными.
Тезис
должен оставаться тождественным, т. е. одним и тем же на протяжении всего доказательства.
Тезис не должен быть логически противоречив.
Тезис не должен противоречить другим суждениям по данному вопросу.
Доводы, приводимые в подтверждение тезиса, не должны противоречить друг другу.
Тезис и доводы должны быть, в конечном счёте, обоснованы фактами.
Доводы, приводимые в подтверждение истинности тезиса, должны являться достаточным основанием для данного тезиса.
Доводы должны быть суждениями, истинность которых доказана независимо от тезиса.
Общее
правило
Правила,
вытекающие
из закона
тождества
Правила,
вытекающие
из закона
запрета
противоречия
Правила,
вытекающие
из закона
достаточного
основания
Слайд 25
Виды доказательства
Прямое доказательство
Прямое доказательство –
доказательство, основывающееся
на каком-нибудь
несомненном начале,
из которого выводится
истинность тезиса.
Следует иметь в виду, что
термин
«прямое доказательство»
в судопроизводстве понимается
иначе, чем в логике, а именно:
прямыми доказательствами
называются показания
свидетелей-очевидцев
преступления или происшествия.
Слайд 26
связка
связка
связка
связка
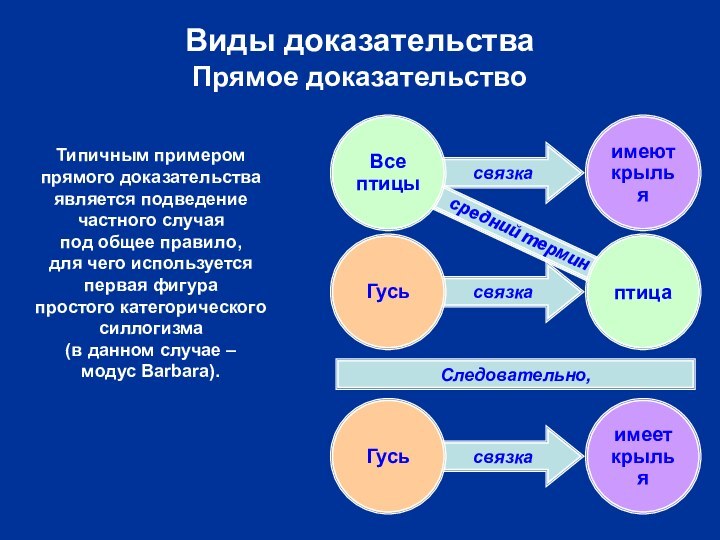
Виды доказательства
Прямое доказательство
Гусь
имеет
крылья
Следовательно,
средний термин
Все
птицы
имеют
крылья
Гусь
птица
Типичным примером
прямого доказательства
является подведение
частного
случая
под общее правило,
для чего используется
первая фигура
простого категорического
силлогизма
(в данном случае
–
модус Barbara).
Слайд 27
связка
связка
не есть
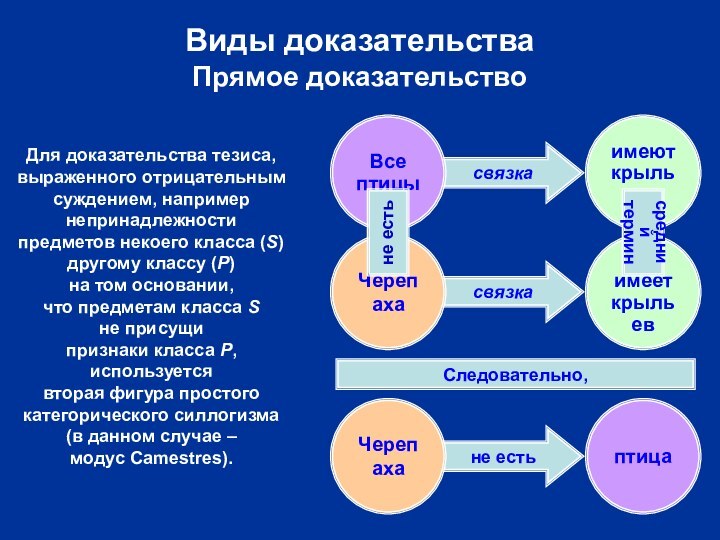
Виды доказательства
Прямое доказательство
Черепаха
птица
Следовательно,
Все
птицы
имеют
крылья
Черепаха
не имеет
крыльев
средний
термин
не есть
Для доказательства тезиса,
выраженного
отрицательным
суждением, например
непринадлежности
предметов некоего класса (S)
другому классу (P)
на том основании,
что
предметам класса S
не присущи
признаки класса P,
используется
вторая фигура простого
категорического силлогизма
(в данном случае –
модус Camestres).
Слайд 28
Виды доказательства
Косвенное доказательство
Косвенное доказательство –
доказательство, в котором истинность
тезиса
обосновывается посредством опровержения
противоречащего положения: вначале доказывается
ложность отрицания предложенного тезиса
и
только после этого, вернее из этого выводится –
на основании закона исключённого третьего –
истинность данного тезиса.
Следует иметь в виду, что термин «косвенное доказательство»
в судопроизводстве понимается иначе, чем в логике, а именно:
косвенными доказательствами называются доказательства,
удостоверяющие искомый факт посредством других фактов,
прямо и непосредственно не свидетельствующих ни против,
ни за обвиняемого, но позволяющих – в совокупности
с другими обстоятельствами дела – определить виновного.
Слайд 29
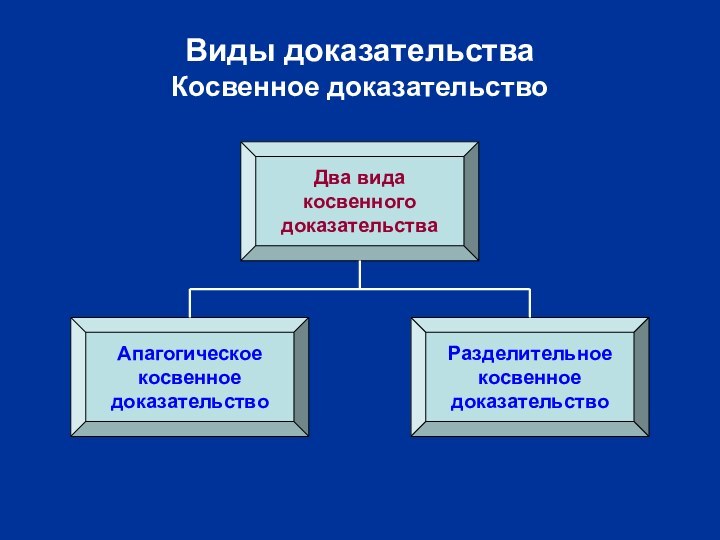
Виды доказательства
Косвенное доказательство
Два вида
косвенного
доказательства
Апагогическое
косвенное
доказательство
Разделительное
косвенное
доказательство
Слайд 30
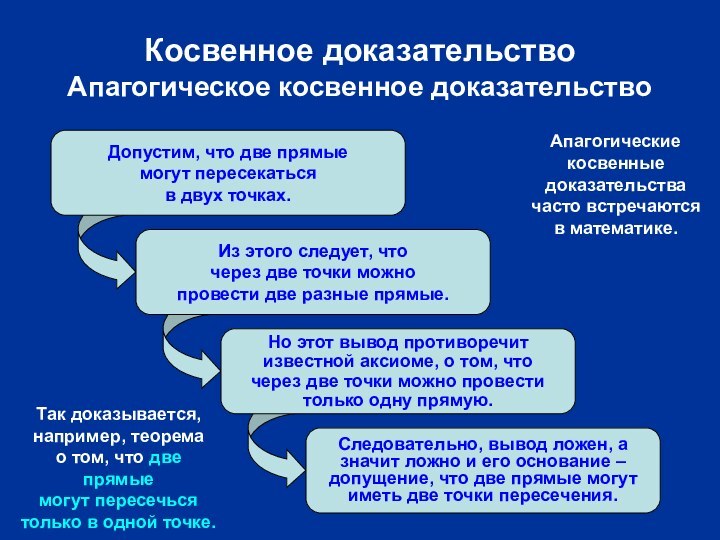
Допустим, что две прямые
могут пересекаться
в двух точках.
Из этого
следует, что
через две точки можно
провести две разные прямые.
Но
этот вывод противоречит
известной аксиоме, о том, что
через две точки можно провести
только одну прямую.
Следовательно, вывод ложен, а
значит ложно и его основание –
допущение, что две прямые могут
иметь две точки пересечения.
Косвенное доказательство
Апагогическое косвенное доказательство
Так доказывается,
например, теорема
о том, что две прямые
могут пересечься
только в одной точке.
Апагогические
косвенные
доказательства
часто встречаются
в математике.
Слайд 31
Косвенное доказательство
Апагогическое косвенное доказательство
Предположим, мы решили доказать, что
все яблоки – красные, «от противного».
Допустив «противный» тезис, что
все яблоки – зелёные, мы без труда докажем его ложность, просто предъявив одно незелёное (красное или жёлтое) яблоко.
Но из ложности утверждения «все яблоки зелёные» не следует истинность утверждения «все яблоки красные»: противные (контрарные) суждения не могут быть оба истинными, но вполне могут оказаться оба ложными.
Для того, чтобы апагогически доказать, что все яблоки – красные, нам следовало бы доказать ложность частноотрицательного суждения «некоторые яблоки не красные» (а это нам не удастся).
Апагогическое косвенное доказательство известно также как
«доказательство от противного», хотя это наименование неточно –
следовало бы называть его «доказательством от противоречащего»
(контрадикторного), поскольку из ложности противного (контрарного)
суждения истинность другого противного суждения не следует.
Слайд 32
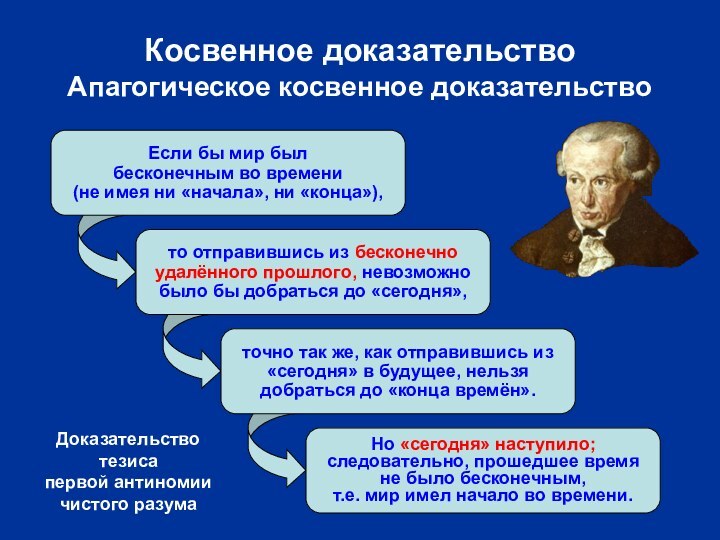
Если бы мир был
бесконечным во времени
(не имея ни
«начала», ни «конца»),
то отправившись из бесконечно
удалённого прошлого, невозможно
было бы
добраться до «сегодня»,
точно так же, как отправившись из
«сегодня» в будущее, нельзя
добраться до «конца времён».
Но «сегодня» наступило;
следовательно, прошедшее время
не было бесконечным,
т.е. мир имел начало во времени.
Косвенное доказательство
Апагогическое косвенное доказательство
Доказательство
тезиса
первой антиномии
чистого разума
Слайд 33
Косвенное доказательство
Апагогическое косвенное доказательство
22 апреля
1724 года
Доказательство
тезиса
Первая антиномия
В
будущее
В прошлое
Из прошлого
Слайд 34
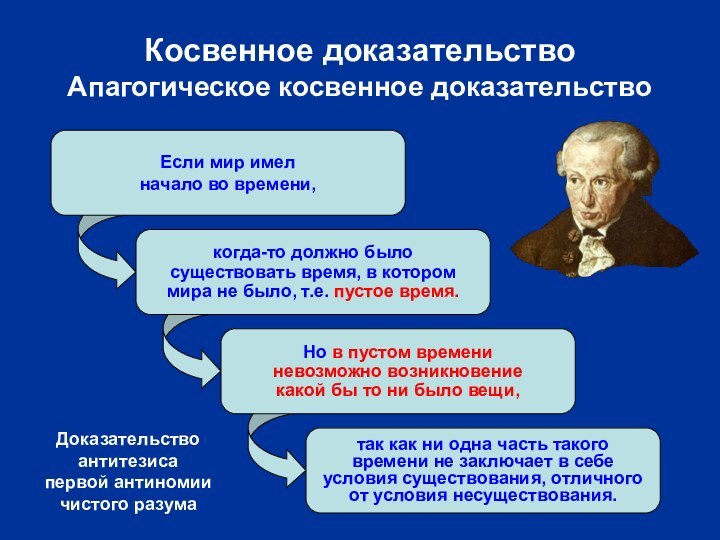
Если мир имел
начало во времени,
когда-то должно было
существовать время,
в котором
мира не было, т.е. пустое время.
Но в пустом
времени
невозможно возникновение
какой бы то ни было вещи,
так как ни одна часть такого
времени не заключает в себе
условия существования, отличного
от условия несуществования.
Косвенное доказательство
Апагогическое косвенное доказательство
Доказательство
антитезиса
первой антиномии
чистого разума
Слайд 35
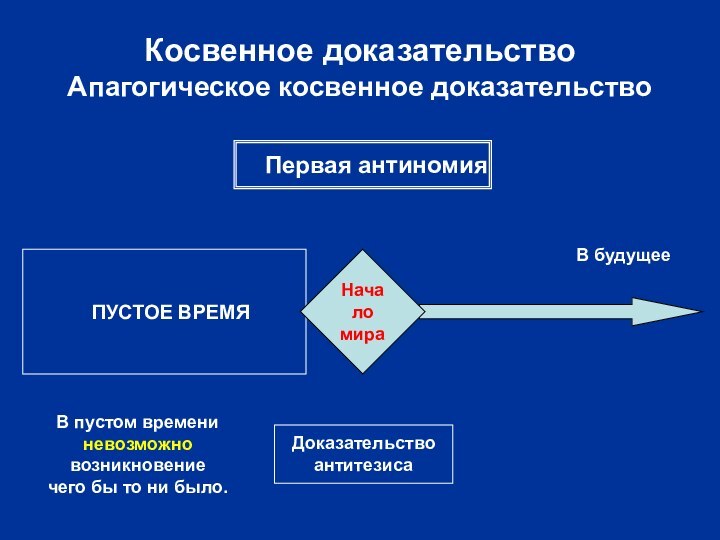
ПУСТОЕ ВРЕМЯ
Косвенное доказательство
Апагогическое косвенное доказательство
Доказательство
антитезиса
Первая антиномия
В
будущее
В пустом времени
невозможно
возникновение
чего бы то ни было.
Начало
мира
Слайд 36
есть
не есть
есть
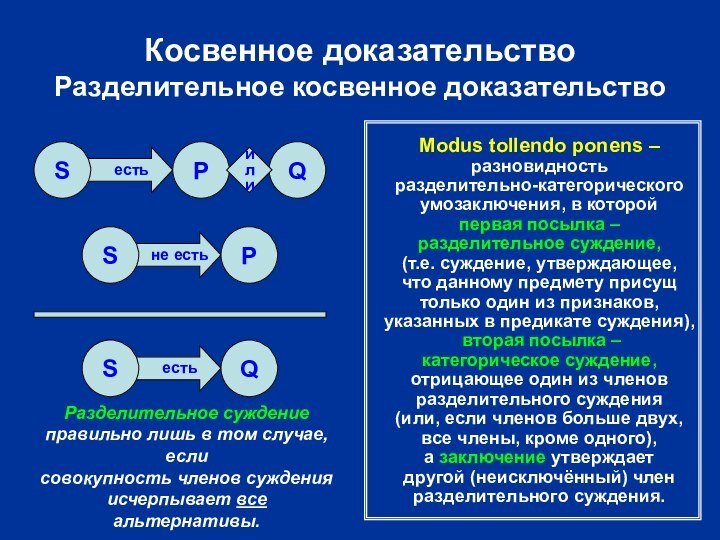
Косвенное доказательство
Разделительное косвенное доказательство
S
P
Q
S
P
S
Q
Modus tollendo ponens –
разновидность
разделительно-категорического
умозаключения,
в которой
первая посылка –
разделительное суждение,
(т.е. суждение, утверждающее,
что данному предмету
присущ
только один из признаков,
указанных в предикате суждения),
вторая посылка –
категорическое суждение,
отрицающее один из членов
разделительного суждения
(или, если членов больше двух,
все члены, кроме одного),
а заключение утверждает
другой (неисключённый) член
разделительного суждения.
Разделительное суждение
правильно лишь в том случае, если
совокупность членов суждения
исчерпывает все альтернативы.
или
Слайд 37
Виды доказательства
Индуктивное и дедуктивное доказательства
Индуктивное доказательство –
одна из
форм доказательства,
когда тезис, являющийся
каким-либо общим суждением,
обосновывается с помощью
единичных или
менее
общих суждений.
Дедуктивное доказательство –
одна из форм доказательства,
когда тезис, являющийся
каким-либо единичным
или частным суждением,
подводится
под общее правило.
При дедуктивном доказательстве
проблема заключается
в следующем:
оппонент должен согласиться,
что общее правило,
под которое подводится
единичный или частный факт,
истинно.
При индуктивном доказательстве
проблема заключается в следующем:
оппонент должен согласиться,
что приведённые в обоснование
общего тезиса единичные или
частные факты исчерпывают
всё множество фактов,
охватываемых общим суждением.
Слайд 38
Понятие опровержения
Определение опровержения
Опровержение –
логическое действие,
в процессе которого
доказывается
ложность
или несостоятельность
какого-либо тезиса.
Из сказанного следует,
что опровержение
представляет собой
специфическую разновидность
доказательства, а
именно:
доказательство не истинности,
а ложности тезиса.
Слайд 39
Основные приёмы опровержения
Прямое (непосредственное) опровержение:
Самый верный и успешный
способ опровержения тезиса, выставленного оппонентом, это опровержение фактами
(«факты
– упрямая вещь»).
Косвенное опровержение:
Подвергаются критике доводы, которые выдвинуты оппонентом в обоснование опровергаемого тезиса.
Доказывается, что опровергаемый тезис не вытекает из доводов, приведённых оппонентом в подтверждение его истинности.
Доказывается, что из опровергаемого тезиса необходимо вытекает следствие, противоречащее истине.
Выдвигается и доказывается новый тезис – противоположный или противоречащий опровергаемому.
Слайд 40
связка
связка
связка
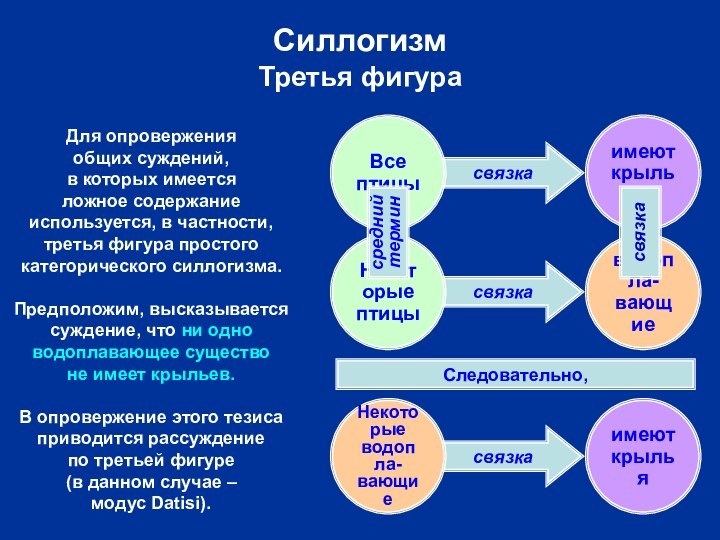
Силлогизм
Третья фигура
Некоторые
водопла-
вающие
имеют
крылья
Следовательно,
Все
птицы
имеют
крылья
Некоторые
птицы
водопла-
вающие
средний
термин
связка
Для опровержения
общих суждений,
в которых имеется
ложное содержание
используется, в
частности,
третья фигура простого
категорического силлогизма.
Предположим, высказывается
суждение, что ни одно
водоплавающее существо
не
имеет крыльев.
В опровержение этого тезиса
приводится рассуждение
по третьей фигуре
(в данном случае –
модус Datisi).