- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ОСНОВЫ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Содержание
- 2. Линейное программирование – это разновидность математического моделирования,
- 3. где
- 4. Слова «наилучшим образом» здесь означают выбор некоторого
- 5. Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат»,
- 6. (1)(2)где - математическая запись критерия оптимальности – целевая функция
- 7. D – область определения задачи. Совокупность чисел
- 8. (4)(5)Условие (5) необязательно, но его всегда при необходимости можно добиться.
- 9. Обозначение говорит о
- 10. В случае линейного программирования целевая функция
- 11. (7)
- 12. Пример 3. Задача о смесях.Стандартом предусмотрено, что
- 14. Требуется определить, сколько тонн каждого компонента следует
- 15. РешениеДля решения этой задачи сформулируем ее экономико-математическую
- 16. ,
- 17. Функциональное ограничение (1) отражает необходимость получения заданного
- 18. Полученная математическая задача-задача линейного программирования. Она может
- 19. Подставляя найденное решение в целевую функцию, имеем(ден.
- 20. Решение систем алгебраических линейных уравнений Метод Крамера
- 21. Рассмотрим систему из n линейных уравнений с n неизвестными (определенная система)
- 22. Определитель системы , составленный из коэффициентов при
- 23. Решением системы (1) называется совокупность чисел
- 24. Решить систему уравнений (1) можно различными методами,
- 25. Теорема КрамераЕсли определитель системы (1) отличен
- 26. В этой формуле является определителем, полученным
- 27. ПримерРешить систему уравнений РешениеОпределитель системы Система имеет единственное решение.
- 28. ОТВЕТ: х = 1,5; у = 0,5
- 29. Однородная система трех линейных уравненийДля простоты полагаем n = 3Однородная система(1)
- 30. Система (1) имеет тривиальное решение:но может случиться,
- 31. ТеоремаЛинейная однородная система трех линейных уравнений с
- 32. ДоказательствоПусть система (1) имеет ненулевое решениеПусть ее
- 33. Это противоречит предположению. Следовательно, = 0.
- 34. ПримерРешить систему уравнений
- 35. Система имеет тривиальное решение:Другой способ расчета:ОТВЕТ: (0, 0, 0)
- 36. ОБРАТНАЯ МАТРИЦА. РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ
- 37. ОпределениеЕсли определитель матрицы А равен нулю,
- 38. Рассмотрим теперь так называемую обратную матрицу, понятие
- 39. ОпределениеПусть дана матрица Составим матрицу
- 40. Матрица называется матрицей, присоединенной к матрице А.
- 41. ТеоремаЕсли матрица А не вырожденная, то она
- 42. На основании теоремы запишем алгоритм получения обратной
- 43. 2. Находим алгебраические дополнения всех элементов
- 44. 4. Умножим полученную матрицу на ПримерНайти матрицу, обратную матрице Решение1. Находим определитель матрицы А:
- 45. Следовательно, данная матрица А является невырожденной и имеет обратную матрицу.2. Найдем алгебраические дополнения каждого элемента:
- 46. Получим матрицу
- 47. Проверим полученный результат:ОТВЕТ:
- 48. РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
- 49. Пусть для простоты n = 3, имеем
- 50. Числа aik коэффициенты системы, а числа
- 51. Введем матрицу коэффициентовХ - вектор-столбец из неизвестных, а В – вектор-столбец свободных членов:
- 52. Согласно правилу умножения матриц данную систему (1) можно записать так:или
- 53. Используя определение равенства матриц, данную систему (1)
- 54. Умножая обе части уравнения (2) слева на
- 55. Итак, чтобы решить матричное уравнение, нужноНайти обратную
- 56. ЗадачаДана система уравнений решить ее матричным способом.
- 57. РешениеЗапишем систему в матричной форме АХ =
- 58. Выпишем все алгебраические дополнения элементов матрицы А:
- 60. Запишем новую матрицу Транспонируем ее: присоединенная матрицаУчитывая,
- 61. 2. Находим произведение Х = А1 В
- 62. 3. Итак,, х1 = 2, х2 = 1, х3 = 3.ОТВЕТ: (2, 1, 3)ЗамечаниеДругой расчет:
- 63. СИСТЕМА m ЛИНЕЙНЫХ УРАВНЕНИЙ С n ПЕРЕМЕННЫМИ
- 64. Рассмотрим систему m линейных с n переменными
- 65. (1)или в краткой записи
- 66. или в векторной записи:где…, соответствующие вектор-столбцы.
- 67. Запишем расширенную матрицу этой системы в виде:
- 68. перестановка любых двух уравнений (строк); умножение обеих
- 69. вычеркивание нулевой строки (уравнения с нулевыми коэффициентами
- 70. Можно показать, что элементарные преобразования переводят данную
- 71. МЕТОД ГАУССА
- 72. Рассмотрим решение системы m линейных уравнений с n переменными:(1)
- 73. Метод Гаусса – метод последовательного исключения переменных
- 74. Предположим, что в системе (1) коэффициент при
- 75. и прибавляя последовательно полученные уравнения соответственно ко
- 76. Получим(2)где буквами с верхним индексом (1) обозначены новые коэффициенты, полученные после первого шага.
- 77. Шаг 2. Предположим, что
- 78. уравнения соответственно к третьему, четвертому, …, m–му
- 79. (3)
- 80. Число нуль в последних m–r уравнениях означает,
- 81. тождествами и их можно не принимать во
- 82. б) б) (в этом случае
- 83. Преобразование Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с расширенной матрицей системы (1)
- 84. ЗадачаРешить систему уравнений:
- 85. РешениеРасширенная матрица системы имеет вид:Шаг 1 Так
- 86. второй, третьей, четвертой строкам, исключим переменную х1
- 87. Шаг 2 Так как теперь
- 88. Шаг 3 Учитывая, что
- 89. Скачать презентацию
- 90. Похожие презентации
























































































Слайд 2
Линейное программирование – это разновидность математического моделирования, частный
случай оптимального программирования.
такое планово-управленческое решениеСлайд 3 где –
его компоненты (параметры), которое наилучшим образом учитывало бы внутренние
возможности и внешние условия производственной деятельности хозяйствующего субъекта.Слайд 4 Слова «наилучшим образом» здесь означают выбор некоторого критерия
оптимальности, т. е. некоторого экономического показателя, позволяющего сравнивать эффективность
тех или иных планово-управленческих решений.Слайд 5 Традиционные критерии оптимальности: «максимум прибыли», «минимум затрат», «максимум
рентабельности» и др.
Таким образом, реализовать на практике принцип оптимальности
в планировании и управлении – это значит решить экстремальную задачу вида: Слайд 7 D – область определения задачи. Совокупность чисел
, удовлетворяющих ограничениям задачи называется допустимым решением (или планом).
Задачу условной оптимизации (1), (2) обычно записывают в виде:
Найти максимум или минимум функции
= (3)
При ограничениях
Слайд 9 Обозначение говорит о том,
что в конкретном ограничении возможен один из знаков:
Задача
(3 – 5) – общая задача оптимального (математического) программирования, иначе – математическая модель задачи оптимального программирования.План , при котором целевая функция задачи принимает максимальное (минимальное) значение, называется оптимальным.
Слайд 10 В случае линейного программирования целевая функция
может быть представлена в
виде линейной формы заданные постоянные величины, а связь с ограниченными ресурсами описывается линейными уравнениями и неравенствами
Слайд 11
(7)
(8)
(6)
Наиболее изучены задачи линейного программирования, для которых разработан универсальный метод решения – метод последовательного улучшения плана (симплекс-метод)
Слайд 12
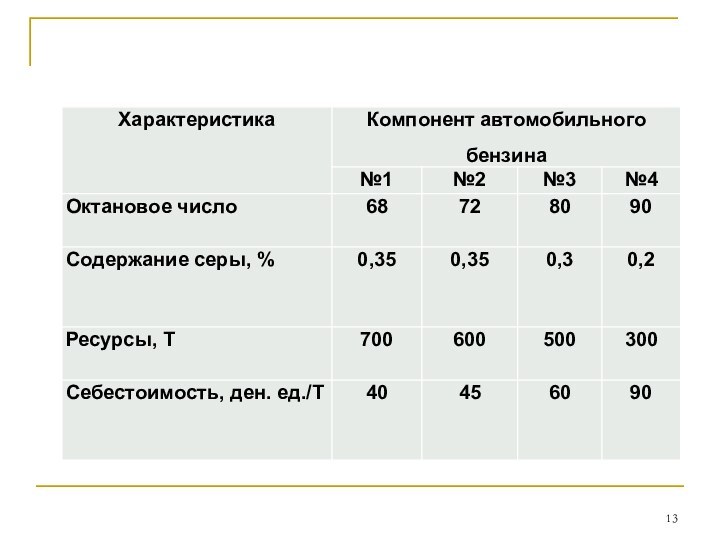
Пример 3. Задача о смесях.
Стандартом предусмотрено, что октановое
число автомобильного бензина А-76 должно быть не ниже 76,
а содержание серы в нем – не более 0,3%. Для изготовления такого бензина на заводе используется смесь из четырех компонентов. Данные о ресурсах смешиваемых компонентов, их себестоимости и их октановом числе, а также о содержании серы приведены в таблице.Слайд 14 Требуется определить, сколько тонн каждого компонента следует использовать
для получения 1000 т автомобильного бензина А-76, чтобы его
себестоимость была минимальной.
Слайд 15
Решение
Для решения этой задачи сформулируем ее экономико-математическую модель.
Введем
необходимые обозначения:
пусть
- количество в смеси компонента с номером j. С учетом этих обозначений имеем задачу (критерий оптимальности – «минимум себестоимости»):Слайд 17 Функциональное ограничение (1) отражает необходимость получения заданного количества
смеси (1000 т), (2), (3) – ограничения по октановому
числу и содержанию серы в смеси, остальные – ограничения на имеющиеся объемы соответствующих ресурсов.Слайд 18 Полученная математическая задача-задача линейного программирования. Она может быть
решена симплекс-методом, который мы рассмотрим позже.
В результате решения получается
оптимальное решениет,
т,
т,
т,
Слайд 19
Подставляя найденное решение в целевую функцию, имеем
(ден. ед.)
Таким
образом, оптимальному решению
будет отвечать минимальная себестоимость в 57160 ден. ед.Слайд 22 Определитель системы , составленный из коэффициентов при неизвестных,
имеет вид
Числа
свободные члены.Система (1) называется однородной, если
Слайд 23 Решением системы (1) называется совокупность чисел
которые обращают все уравнения в тождества.
Система имеющая хотя бы одно решение, называется совместной.
Система, не имеющая решений, называется несовместной.
Слайд 24 Решить систему уравнений (1) можно различными методами, в
частности, методом Крамера (Крамер – швейцарский математик, 1704 –
1752)
Слайд 25
Теорема Крамера
Если определитель системы (1) отличен от
нуля, то система совместна и имеет единственное решение, которое
можно найти по формуле:Слайд 26 В этой формуле является определителем, полученным из
определителя системы путем замены столбца j столбцом свободных
членов.Замечание
Если определитель системы уравнений (1) = 0, то система (1) или несовместна или имеет бесконечно много решений.
Слайд 27
Пример
Решить систему уравнений
Решение
Определитель системы
Система имеет единственное
решение.
Слайд 30
Система (1) имеет тривиальное решение:
но может случиться, что
однородная система (1) имеет и не нулевое решение. Его
называют нетривиальным решением однородной системы (1).
Слайд 31
Теорема
Линейная однородная система трех линейных уравнений с 3
неизвестными имеет ненулевое решение тогда и только тогда, когда
ее определитель = 0, т. е.
Слайд 32
Доказательство
Пусть система (1) имеет ненулевое решение
Пусть ее определитель
0, тогда на основании формул Крамера система
(1) имеет только нулевое решениеСлайд 33 Это противоречит предположению. Следовательно, = 0. Тогда
линейная система (1) либо несовместна, либо имеет бесконечно много
решений. Но наша система совместна, так как имеется нулевое решение. Следовательно, система (1) допускает бесконечно много решений, в том числе и ненулевые.
Слайд 37
Определение
Если определитель матрицы А равен нулю, то
матрица А называется вырожденной; в противном случае матрица А
называется невырожденной.Слайд 38 Рассмотрим теперь так называемую обратную матрицу, понятие которой
вводится только для квадратной матрицы.
Определение
Если А – квадратная матрица,
то обратной для нее матрицей называется матрица, обозначенная А-1 и удовлетворяющая условиям , где Е – единичная матрица
Слайд 39
Определение
Пусть дана матрица
Составим матрицу из
алгебраических дополнений к элементам транспонированной матрицы :
Слайд 41
Теорема
Если матрица А не вырожденная, то она имеет
обратную матрицу, которая находится по формуле
или
где
- матрица, присоединенная к матрице А,
Слайд 42
На основании теоремы запишем алгоритм получения обратной матрицы:
1.
Находим определитель матрицы А:
Если
, то обратная матрица не существует. Если , то переходим ко 2 шагу.
Слайд 43 2. Находим алгебраические дополнения всех элементов
матрицы А и записываем новую матрицу составленную из
(алгебраических дополнений).3. Транспонируем полученную матрицу (меняем местами столбцы полученной матрицы со строками), получаем присоединенную матрицу .
Слайд 44
4. Умножим полученную матрицу на
Пример
Найти
матрицу, обратную матрице
Решение
1. Находим определитель матрицы А:
Слайд 45 Следовательно, данная матрица А является невырожденной и имеет
обратную матрицу.
2. Найдем алгебраические дополнения каждого элемента:
Слайд 46 Получим матрицу
алгебраических дополнений
3. Транспонируем эту
матрицу, получаем присоединенную матрицу . 4. Умножим полученную матрицу на , т. е. на
Слайд 49 Пусть для простоты n = 3, имеем систему
линейных уравнений (определенная система: 3
уравнения, 3 неизвестных):(1)
Слайд 50 Числа aik коэффициенты системы, а числа bi
свободные члены, i = 1, 3, k =
1, 3.Решением системы (1) называется совокупность чисел x1 = 1, x2 = 2, x3 = 3, которые обращают все уравнения системы в тождества.
Слайд 51
Введем матрицу коэффициентов
Х - вектор-столбец из неизвестных, а
В – вектор-столбец свободных членов:
Слайд 53 Используя определение равенства матриц, данную систему (1) можно
записать в виде матричного уравнение
АХ = В ,
(1)Здесь в роли неизвестного выступает матрица Х. Уравнение (2) решается следующим образом. Если А – невырожденная матрица ( ), то можно определить обратную матрицу А1 .
Слайд 54 Умножая обе части уравнения (2) слева на А1
А1 АХ = А1 В
используем сочетательный закон умножения:
(А1 А
)Х = А1 В , но так как А1 А = Е , то получаем решение матричного уравнения (2) в виде Х = А1В.
Слайд 55
Итак, чтобы решить матричное уравнение, нужно
Найти обратную матрицу
А1
Найти произведение А1 В = Х
Пользуясь определением равных матриц,
записать ответ.
Слайд 57
Решение
Запишем систему в матричной форме АХ = В:
Решение системы Х = А1В
1. Найдем обратную матрицу А1
Слайд 60
Запишем новую матрицу
Транспонируем ее:
присоединенная матрица
Учитывая, что
, запишем обратную
матрицуСлайд 64 Рассмотрим систему m линейных с n переменными (при
m < n такие системы называются неопределенными):
Число уравнений
m не равно, вообще говоря, числу неизвестных n.Слайд 67 Запишем расширенную матрицу этой системы в виде: А1
А2 … Аn
BЭлементарными преобразованиями системы (1) (или матрицы Ар) называются следующие преобразования:
Слайд 68
перестановка любых двух уравнений (строк);
умножение обеих частей
одного из уравнений на любое отличное от нуля число;
прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число, отличное от нуля; Слайд 69 вычеркивание нулевой строки (уравнения с нулевыми коэффициентами и
свободным членом, равным 0):
Определение.
Системы уравнений вида (1) называются
эквивалентными (или равносильными), если они имеют одно и то же множество решений.Слайд 70 Можно показать, что элементарные преобразования переводят данную систему
уравнений в эквивалентную систему.
При практическом решении системы линейных
уравнений методом Гаусса последовательно над строками матрицы Ар выполняют элементарные преобразования, так что некоторое неизвестное исключается из всех уравнений, кроме одного, т. е. в составе расширенной матрицы формируется единичная матрица.Слайд 73 Метод Гаусса – метод последовательного исключения переменных –
заключается в том, что с помощью элементарных преобразований система
уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.Слайд 74 Предположим, что в системе (1) коэффициент при переменной
х1 в первом уравнении а11 0 (если это
не так, то перестановкой уравнений местами добьемся того, что а11 0 ).Шаг 1. Умножая первое уравнение на подходящие числа (а именно на )
…,
Слайд 75 и прибавляя последовательно полученные уравнения соответственно ко второму,
третьему, …, m–му уравнению системы (1), исключим переменную х1
из всех последующих уравнений, начиная со второго.
Слайд 76
Получим
(2)
где буквами с верхним индексом (1) обозначены новые
коэффициенты, полученные после первого шага.
Слайд 77
Шаг 2.
Предположим, что
(если не так, то соответствующей перестановкой
уравнений или переменных с изменением их номеров добьемся того, чтобы . Умножая второе уравнение последовательно на подходящие числа…,
и прибавляя полученные
Слайд 78 уравнения соответственно к третьему, четвертому, …, m–му уравнению
системы, исключим переменную х2 из всех последующих уравнений, начиная
с третьего.Продолжая процесс последовательного исключения переменных, после (r1)-го шага получим систему
Слайд 80 Число нуль в последних m–r уравнениях означает, что
их левые части имеют вид:
Если хотя бы одно
из чисел , … , не равны нулю, то соответствующее равенство противоречиво, и система (1) несовместна. Таким образом, для любой совместной системы числа , …, в системе (3) равны нулю. В этом случае m–r уравнений в системе (3) являются
Слайд 81 тождествами и их можно не принимать во внимание
при решении системы (1).
Очевидно, что после отбрасывания «лишних» уравнений
возможны два случая:а) число уравнений системы (3) равно числу переменных т. е. r = n (в этом случае система (3) имеет треугольный вид);
Слайд 82
б)
б) (в этом случае
система (3) имеет ступенчатый вид).
Переход системы (1) к равносильной
ей системе (3) называется прямым ходом метода Гаусса, а нахождение переменных из системы (3) – обратным ходом.Слайд 83 Преобразование Гаусса удобно проводить, осуществляя преобразования не с
самими уравнениями, а с расширенной матрицей системы (1)
Слайд 85
Решение
Расширенная матрица системы имеет вид:
Шаг 1 Так как
a11 0. То умножая первую строку последовательно на
числа (2), (3), (2) и прибавляя полученные строки соответственно коСлайд 86 второй, третьей, четвертой строкам, исключим переменную х1 из
всех строк, начиная со второй.
Заметив, что в новой
матрице , поменяем местами вторую и третью строки: ̴
Слайд 87 Шаг 2 Так как теперь
, то
умножая вторую строку на и прибавляя полученную строку к четвертой, исключим переменную х2 из всех строк, начиная с третьей: ̴
Слайд 88 Шаг 3 Учитывая, что
, умножая третью строку на
и прибавляя полученную строку к четвертой исключим из нее переменную х3.Получим (см. последнюю матрицу) систему уравнений