Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Параллельноепроектирование и изображение пространственных фигур

Содержание

ПланЧто такое параллельное проектированиеНаправление проектированияОсновные свойства параллельного проектированияТеоремы о параллельности и сохранении пропорциональностиПримеры и решение задачОртогональное проектирование
Параллельное проектирование и изображение пространственных фигур Автор Календарева Н.Е.© 2011 г. ПланЧто такое параллельное проектированиеНаправление проектированияОсновные свойства параллельного проектированияТеоремы о параллельности и сохранении Что такое параллельное проектированиеДля изображения пространственных фигур на плоскости обычно используют параллельное Направление проектиро- ванияВ рассматриваемых далее примерах такая прямая выбрана случайным образом.Параллельное проектирование Пусть даны две различные плоскости α и β и прямая m, не Выберем направление проектирования, в нашем примере – это прямая m. Проектирование параллельно прямой m Основные свойстваПользуемся правилами:точка => точку;отрезок => отрезок;луч => луч.Прямая, не || прямой Основные свойстваЕсли в плоскости α есть параллельные прямые, то они проектируются в УтверждениеПараллельные отрезки пространственной фигуры изображаются на плоскости чертежа параллельными отрезками.mα ТеоремаПри параллельном проектировании отношение отрезков одной прямой или параллельных прямых сохраняется. ДоказательствоДокажем, что АВ : ВС = А1В1 : В1С1 .Док-воследуетиз теоремыФалеса. Отношение отрезков есть отношение пропорциональности. Поэтому говорят так: отношение пропорциональности параллельных Известно, что точка пересечения медиан в треугольнике делит медиану в отношении 2 ВопросПроизвольный треугольник в общем случае проектируется в произвольный треугольник.Можно ли спроектировать произвольный Частный пример проектированияДан произвольныйтреугольник.Направлениепроектированияизначально не дано.Его проекция –равностороннийтреугольник. Основные свойства проектированияСередины отрезков проектируются в середины отрезков.Углы при параллельном проектировании не сохраняются. ПримерыВ примерах будут даны два изображения.Слева то изображение, которое мы видим в Что можно строить на про-странственном изображенииНа изображении пространственной фигуры с использованием На плоскости В пространстве На плоскости В пространстве На плоскости В пространстве На плоскости В пространстве На плоскости В пространстве На плоскости В пространстве На плоскости В пространстве Устные задачи1. Дана параллельная проекция треугольника. Чем изобразится проекция средней линии Параллельное проектирование4. Может ли проекция параллелограмма быть квадратом?5. 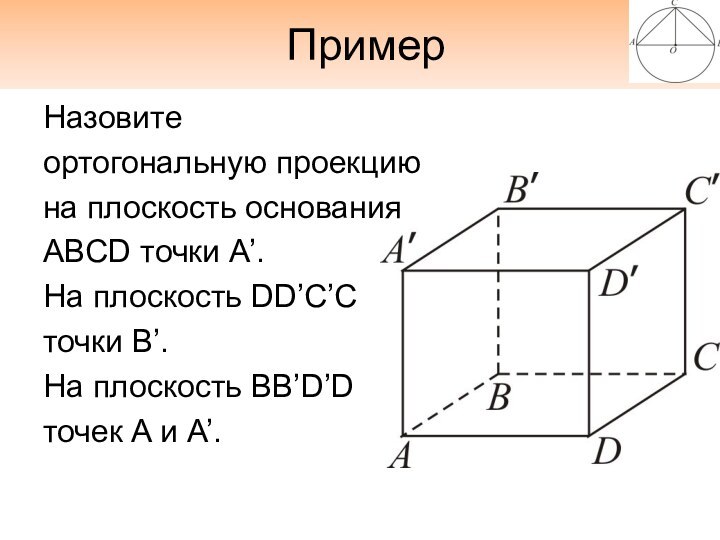Может ли отрезок Ортогональное проектированиеВ задачах, связанных с многогранниками, часто приходится проектировать на определенную ПримерНазовитеортогональную проекциюна плоскость основанияABCD точки А’.На плоскость DD’C’Cточки В’.На плоскость BB’D’Dточек A и A’.
Слайды презентации

Слайд 2 План
Что такое параллельное проектирование
Направление проектирования
Основные свойства параллельного проектирования
Теоремы

ПланЧто такое параллельное проектированиеНаправление проектированияОсновные свойства параллельного проектированияТеоремы о параллельности и

о параллельности и сохранении пропорциональности
Примеры и решение задач
Ортогональное проектирование

Слайд 3 Что такое параллельное проектирование
Для изображения пространственных фигур на

Что такое параллельное проектированиеДля изображения пространственных фигур на плоскости обычно используют

плоскости обычно используют параллельное проектирование. При параллельном проектировании обязательно

необходимо задавать направление проектирования, т. е. некоторую прямую в пространстве.

Слайд 4 Направление проектиро- вания
В рассматриваемых далее примерах такая прямая выбрана

Направление проектиро- ванияВ рассматриваемых далее примерах такая прямая выбрана случайным образом.Параллельное

случайным образом.
Параллельное проектирование соответствует зрительному восприятию фигуры при рассматривании

ее издали.

Слайд 5 Пусть даны две различные плоскости α и β

Пусть даны две различные плоскости α и β и прямая m,

и прямая m, не параллельная ни одной из них.

Будем проектировать точки, например плоскости α на плоскость β параллельно прямой m.
Рассмотрим, в какие фигуры проектируются известные нам фигуры.


Слайд 6 Выберем направление проектирования, в нашем примере – это

Выберем направление проектирования, в нашем примере – это прямая m.

прямая m.

Слайд 7 Проектирование параллельно прямой m

Проектирование параллельно прямой m

Слайд 8 Основные свойства
Пользуемся правилами:
точка => точку;
отрезок => отрезок;
луч =>

Основные свойстваПользуемся правилами:точка => точку;отрезок => отрезок;луч => луч.Прямая, не ||

луч.
Прямая, не ||
прямой m, => в прямую.
Прямая, ||

прямой m, => в точку.
Окружность проектируется в эллипс.

Слайд 9 Основные свойства
Если в плоскости α есть параллельные прямые,

Основные свойстваЕсли в плоскости α есть параллельные прямые, то они проектируются

то они проектируются в параллельные между собой прямые.
Сформулируем это

утверждение и докажем его.


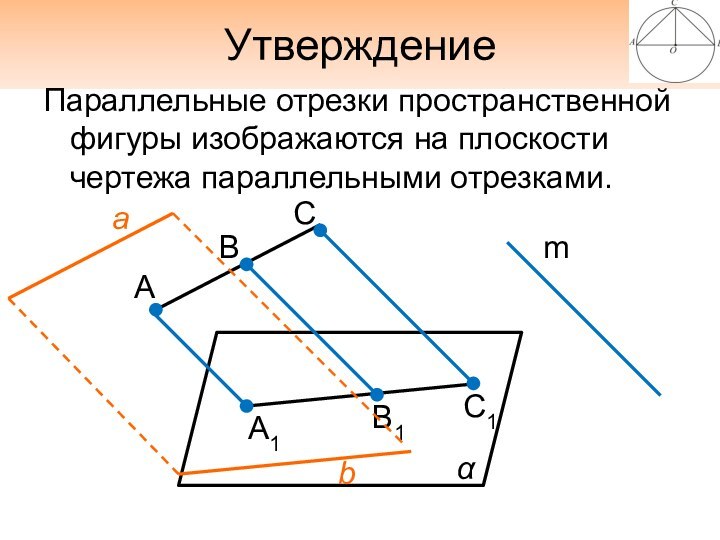
Слайд 10 Утверждение
Параллельные отрезки пространственной фигуры изображаются на плоскости чертежа

УтверждениеПараллельные отрезки пространственной фигуры изображаются на плоскости чертежа параллельными отрезками.mα

параллельными отрезками.
m
α

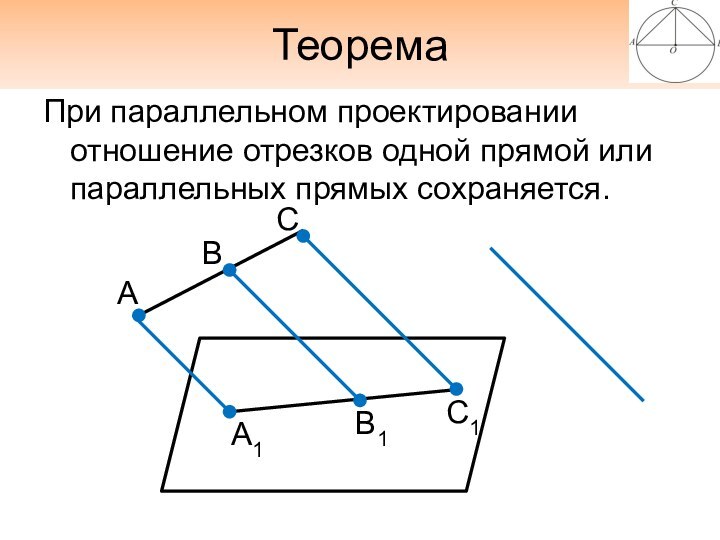
Слайд 11 Теорема
При параллельном проектировании отношение отрезков одной прямой или

ТеоремаПри параллельном проектировании отношение отрезков одной прямой или параллельных прямых сохраняется.

параллельных прямых сохраняется.

Слайд 12 Доказательство
Докажем, что АВ : ВС = А1В1 :

ДоказательствоДокажем, что АВ : ВС = А1В1 : В1С1 .Док-воследуетиз теоремыФалеса.

В1С1 .
Док-во
следует
из теоремы
Фалеса.

Слайд 13 Отношение отрезков есть отношение пропорциональности. Поэтому говорят так:

Отношение отрезков есть отношение пропорциональности. Поэтому говорят так: отношение пропорциональности


отношение пропорциональности параллельных отрезков при параллельном проектировании

сохраняется.
Тогда
середина отрезка проектируется в
середину отрезка.

Слайд 14 Известно, что точка пересечения медиан в треугольнике делит

Известно, что точка пересечения медиан в треугольнике делит медиану в отношении

медиану в отношении 2 : 1, считая от вершины.

Следовательно, при изображении такое же отношение для медиан сохраняется.

Слайд 15 Вопрос
Произвольный треугольник в общем случае проектируется в произвольный

ВопросПроизвольный треугольник в общем случае проектируется в произвольный треугольник.Можно ли спроектировать

треугольник.
Можно ли спроектировать произвольный треугольник в равносторонний?

Ответ: да, можно.

Слайд 16 Частный пример проектирования
Дан произвольный
треугольник.
Направление
проектирования
изначально не дано.
Его проекция –
равносторонний
треугольник.

Частный пример проектированияДан произвольныйтреугольник.Направлениепроектированияизначально не дано.Его проекция –равностороннийтреугольник.

Слайд 17 Основные свойства проектирования
Середины отрезков проектируются в середины отрезков.

Углы при

Основные свойства проектированияСередины отрезков проектируются в середины отрезков.Углы при параллельном проектировании не сохраняются.

параллельном проектировании не сохраняются.

Слайд 18 Примеры
В примерах будут даны два изображения.
Слева то изображение,

ПримерыВ примерах будут даны два изображения.Слева то изображение, которое мы видим

которое мы видим в плоскости тетради, при этом лист

тетради совпадает с плоскостью доски.
Справа дано изображение в пространстве, нарисованное на плоскости доски. Визуально оно не совпадает с первым изображением, это проекция фигуры.

Слайд 19 Что можно строить на про-странственном изображении
На изображении

Что можно строить на про-странственном изображенииНа изображении пространственной фигуры с

пространственной фигуры с использованием параллельного проектирования можно
проводить прямые, параллельные

данным;
делить отрезок в заданном отношении (в том числе пополам);
проводить произвольные отрезки (хорды).

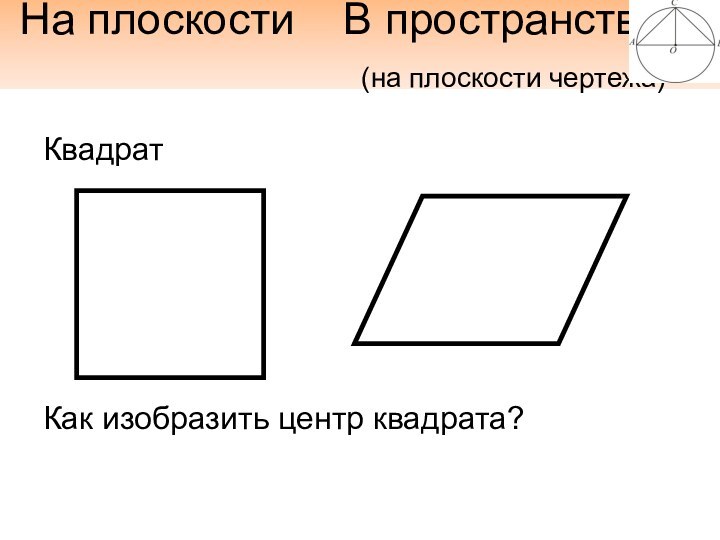
Слайд 20 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)

Равнобедренный Изображение
треугольник равнобедренного тр.





Как изобразить высоту из вершины В?

В

В

Слайд 21 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)






Углы при параллельном проектировании не сохраняются!

Слайд 22 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)

Квадрат





Как изобразить центр квадрата?

Слайд 23 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)

Дано изображение равностороннего треугольника.
Изобразите его центр.

Слайд 24 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)

Изобразите центр окружности





Как построить проекцию диаметра окружности, перпендикулярного заданному?


О

Слайд 25 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)

Дано изображение середин сторон квадрата. Постройте изображение квадрата.

Слайд 26 На плоскости В пространстве

На плоскости В пространстве

(на плоскости чертежа)

Постройте изображение параллелограмма ABCD по изображению вершины А и середин сторон BC и CD.

Слайд 27 Устные задачи
1. Дана параллельная проекция треугольника. Чем

Устные задачи1. Дана параллельная проекция треугольника. Чем изобразится проекция средней

изобразится проекция средней линии треугольника?
2. Каким многоугольником является параллельная

проекция трапеции?
3. Может ли при параллельном проектировании параллелограмма получится трапеция?

Слайд 28 Параллельное проектирование
4. Может ли проекция параллелограмма быть

Параллельное проектирование4. Может ли проекция параллелограмма быть квадратом?5. Может ли

квадратом?
5. Может ли отрезок быть проекцией треугольника?
6. Чем является

проекция ромба?
7. Во что проектируется прямоугольник?

Слайд 29 Ортогональное проектирование
В задачах, связанных с многогранниками, часто

Ортогональное проектированиеВ задачах, связанных с многогранниками, часто приходится проектировать на

приходится проектировать на определенную плоскость.
Если проектируем параллельно прямой, перпендикулярной

этой плоскости, то говорят об ортогональном (перпендикулярном) проектировании. Саму плоскость называют плоскостью проекции.

Слайд 30 Пример
Назовите
ортогональную проекцию
на плоскость основания
ABCD точки А’.
На плоскость

ПримерНазовитеортогональную проекциюна плоскость основанияABCD точки А’.На плоскость DD’C’Cточки В’.На плоскость BB’D’Dточек A и A’.

DD’C’C
точки В’.
На плоскость BB’D’D
точек A и A’.

  • Имя файла: parallelnoeproektirovanie-i-izobrazhenie-prostranstvennyh-figur.pptx
  • Количество просмотров: 110
  • Количество скачиваний: 0
- Предыдущая Практикум по решению задач
Следующая - История Древней Греции

Похожие презентации

Введение о патенте Введение о патенте 226
Шаблон для создания презентаций Новогодний презентация к уроку (1, 2, 3, 4 класс) Шаблон для создания презентаций Новогодний презентация к уроку (1, 2, 3, 4 класс) 87
Постулати Бора.Модель атома кисеню по Бору. Постулати Бора.Модель атома кисеню по Бору. 81
Энциклопедия одного слова Энциклопедия одного слова 113
Прощание с 1 классом материал (1 класс) Прощание с 1 классом материал (1 класс) 109
Анализ работы за 2012-2013 учебный год материал (младшая группа) по теме Анализ работы за 2012-2013 учебный год материал (младшая группа) по теме 107
prezentatsiya microsoft office powerpoint prezentatsiya microsoft office powerpoint 107
История Спасо Вифанского монастыря презентация к занятию (подготовительная группа) История Спасо Вифанского монастыря презентация к занятию (подготовительная группа) 104
Презентация детская агрессивность презентация к уроку по теме Презентация детская агрессивность презентация к уроку по теме 107
Аэродинамика тепловых установок Аэродинамика тепловых установок 106
Презентация. Профессии. презентация к уроку Презентация. Профессии. презентация к уроку 134
Введение в естествознание Введение в естествознание 174
Презентация Моя родина- село кизильское. презентация к уроку (подготовительная группа) Презентация Моя родина- село кизильское. презентация к уроку (подготовительная группа) 149
Тыквеные овощи Тыквеные овощи 133
Лекция 1Понятие риска экономической деятельности Лекция 1Понятие риска экономической деятельности 107
Физминутка Лови снежинку материал Физминутка Лови снежинку материал 182
Анализ генной экспрессии на модели mycoplasmagallisepticum. Анализ генной экспрессии на модели mycoplasmagallisepticum. 93
интерактивная игра Курочка ряба презентация урока для интерактивной доски (средняя группа) интерактивная игра Курочка ряба презентация урока для интерактивной доски (средняя группа) 205
Оценка технических свойств древесины и материалов Оценка технических свойств древесины и материалов 96
Қадыр Мырза Әлі, Тұманбай Молдағалиев Қадыр Мырза Әлі, Тұманбай Молдағалиев 311
Комбинаторика Комбинаторика 98
Функции и структура ЛЭС. Оформление трассы Функции и структура ЛЭС. Оформление трассы 149
Последовательное и параллельное подчинение придаточных Последовательное и параллельное подчинение придаточных 102
Постановка цілей та планування часу Постановка цілей та планування часу 99
Презентация к самоанализу о проделанной работе. презентация по теме Презентация к самоанализу о проделанной работе. презентация по теме 108
Презентация социального проекта От чистого сердца Презентация социального проекта От чистого сердца 95
Мои достижения. Мои достижения. 103
Тема:Творог Тема:Творог 189
Мастер класс по изготовлению Снеговика из носка творческая работа учащихся по конструированию, ручному труду (младшая группа) Мастер класс по изготовлению Снеговика из носка творческая работа учащихся по конструированию, ручному труду (младшая группа) 142
Презентация Проектная деятельность в ДОУ презентация Презентация Проектная деятельность в ДОУ презентация 116