Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Параллельность плоскостей

Содержание

Признак параллельности плоскостейТеорема. Если 2 пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то такие плоскости параллельны
Параллельность плоскостейОпределение.Две плоскости называются параллельными, если они не имеют общих точек, то есть не пересекаютсяαβ Признак параллельности плоскостейТеорема. Если 2 пересекающиеся прямые одной плоскости соответственно параллельны двум αβаbcАВd αβДоказательство: аbcdfАВ αβДоказательство: аbc2. Так как df, топо признаку параллельности прямой и плоскостиАВСледовательно, Так αβДоказательство: аbc4. Так как df, топо признаку параллельности прямой и плоскостиАВСледовательно, Так αβДоказательство: аbc 7. Значит, допущение неверно. df АВСледовательно, 6. Получилось, Свойства параллельных плоскостейαβγ 1 свойствоЕсли две параллельные плоскости пересекаются третьей, то прямые пересечения параллельныab 1 свойствоЕсли две параллельные плоскости пересекаются третьей, то прямые пересечения параллельныДоказательство: 2 свойствоОтрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны 2 свойствоОтрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равныПоэтому, противолежащие стороны
Слайды презентации

Слайд 2 Признак параллельности плоскостей
Теорема.

Если 2 пересекающиеся прямые
одной

Признак параллельности плоскостейТеорема. Если 2 пересекающиеся прямые одной плоскости соответственно параллельны

плоскости
соответственно параллельны
двум пересекающимся прямым
другой плоскости, то


такие плоскости параллельны

Слайд 3 α
β
а
b
c
А
В
d

αβаbcАВd

Слайд 4 α
β
Доказательство:
а
b
c
d
f
А
В

αβДоказательство: аbcdfАВ

Слайд 5 α
β
Доказательство:
а
b
c
2. Так как
d
f
, то
по признаку параллельности

αβДоказательство: аbc2. Так как df, топо признаку параллельности прямой и плоскостиАВСледовательно,

прямой и плоскости
А
В
Следовательно,
Так как они находятся в одной

плоскости α и не пересекаются

Слайд 6 α
β
Доказательство:
а
b
c
4. Так как
d
f
, то
по признаку параллельности

αβДоказательство: аbc4. Так как df, топо признаку параллельности прямой и плоскостиАВСледовательно,

прямой и плоскости
А
В
Следовательно,
Так как они находятся в одной

плоскости α и не пересекаются

Слайд 7 α
β
Доказательство:
а
b
c

7. Значит, допущение неверно.
d
f

αβДоказательство: аbc 7. Значит, допущение неверно. df АВСледовательно, 6.





А
В
Следовательно,

6. Получилось, что через

точку А проходят две прямые а и b,
параллельные прямой f, что противоречит теореме 2.1

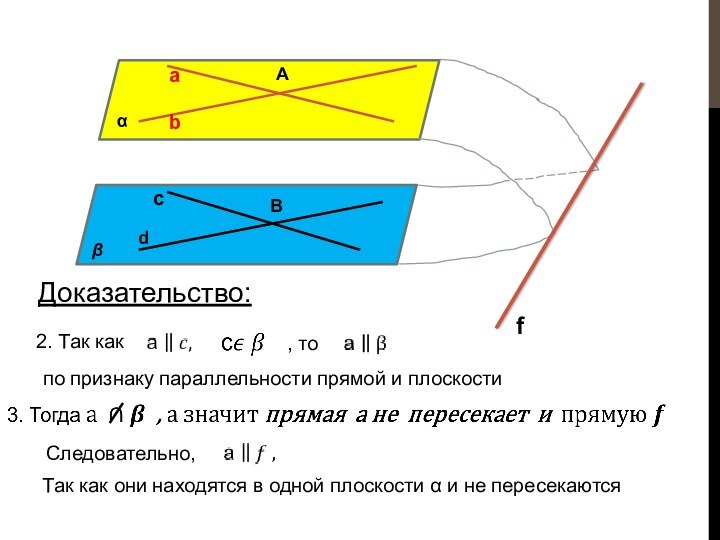
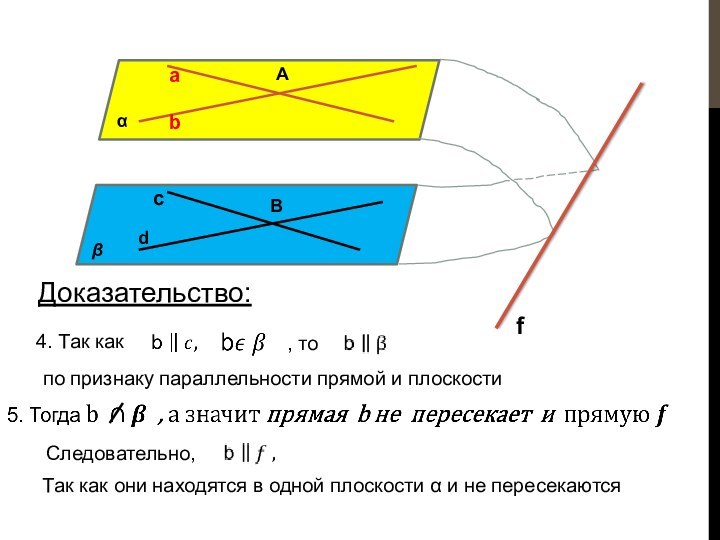
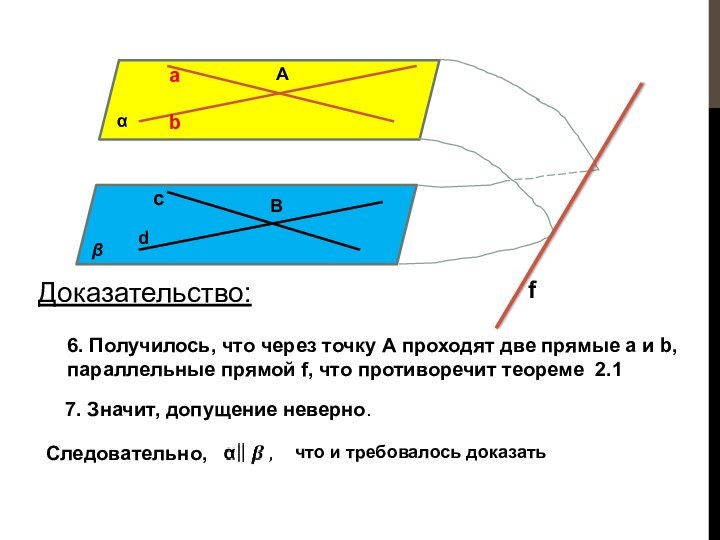
что и требовалось доказать

Слайд 8 Свойства параллельных плоскостей
α
β
γ

Свойства параллельных плоскостейαβγ

Слайд 9 1 свойство
Если две параллельные плоскости пересекаются третьей, то

1 свойствоЕсли две параллельные плоскости пересекаются третьей, то прямые пересечения параллельныab

прямые пересечения параллельны
a
b

Слайд 10 1 свойство
Если две параллельные плоскости пересекаются третьей, то

1 свойствоЕсли две параллельные плоскости пересекаются третьей, то прямые пересечения параллельныДоказательство:

прямые пересечения параллельны
Доказательство:


a
b
Значит, прямые а и b

не пересекаются

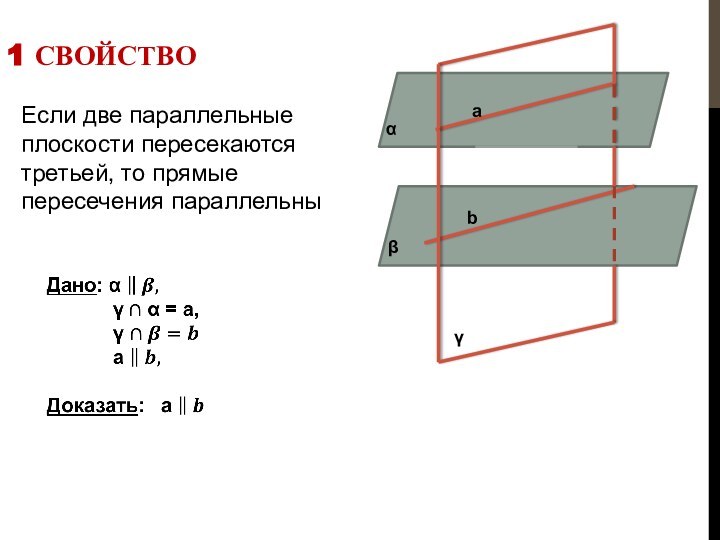
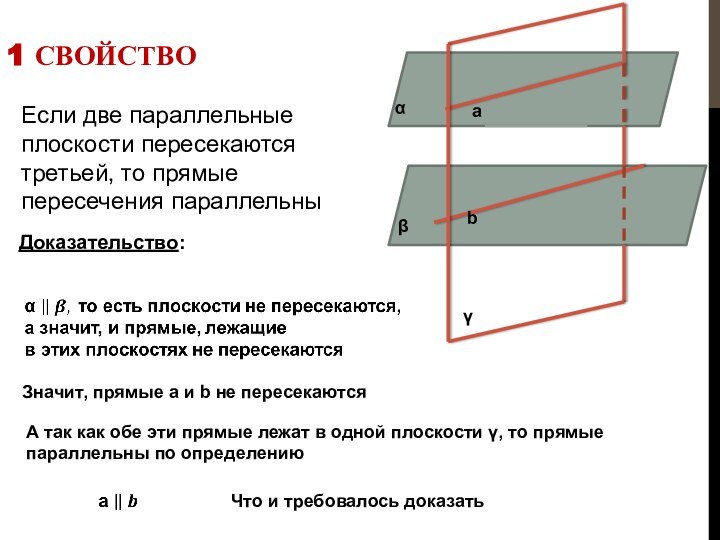
А так как обе эти прямые лежат в одной плоскости γ, то прямые параллельны по определению

Что и требовалось доказать

Слайд 11 2 свойство
Отрезки параллельных прямых, заключённые между двумя параллельными

2 свойствоОтрезки параллельных прямых, заключённые между двумя параллельными плоскостями, равны

плоскостями, равны

  • Имя файла: parallelnost-ploskostey.pptx
  • Количество просмотров: 100
  • Количество скачиваний: 0
- Предыдущая Профессия – Логистик
Следующая - Мотивы, мотивация, потребности, классификация потребностей Маслоу

Похожие презентации

Кошка Кошка 106
Биологическое значение боли Биологическое значение боли 101
Протоколы маршрутизации Протоколы маршрутизации 137
Родными тропами Родными тропами 127
Театрализованная деятельность в детском саду (старшая группа). Презентация. презентация к уроку (старшая группа) Театрализованная деятельность в детском саду (старшая группа). Презентация. презентация к уроку (старшая группа) 116
Шаблон для создания презентации по любой теме По номерам Шаблон для создания презентации по любой теме По номерам 93
Шаблон презентации Шаблон презентации 98
Содержание и направленность работ Керженцева, Ерманского и Амосова Содержание и направленность работ Керженцева, Ерманского и Амосова 106
Фестиваль семейного творчества Семья - счастливая планета. методическая разработка (младшая группа) Фестиваль семейного творчества Семья - счастливая планета. методическая разработка (младшая группа) 86
Презентация по Истории и культуре Курского края на тему Истоки топонимики Курского края Презентация по Истории и культуре Курского края на тему Истоки топонимики Курского края 142
Загадки Афанасия Фета Загадки Афанасия Фета 110
Спортивное развлечение на 23 февраля в средней Г презентация к уроку (средняя группа) по теме Спортивное развлечение на 23 февраля в средней Г презентация к уроку (средняя группа) по теме 44
prezentatsiya samoanalizasaveleva prezentatsiya samoanalizasaveleva 113
Использование мобильного телефона во время занятий Использование мобильного телефона во время занятий 89
Тренинговое занятие для педагогов по профилактике эмоционального выгорания материал по теме Тренинговое занятие для педагогов по профилактике эмоционального выгорания материал по теме 103
Тема. Налог на добавленную стоимость Тема. Налог на добавленную стоимость 104
Презентация проекта Собака-друг человека презентация к уроку (старшая группа) Презентация проекта Собака-друг человека презентация к уроку (старшая группа) 117
Консультация для воспитателей Развитие связной речи – ТРИЗ - технология консультация Консультация для воспитателей Развитие связной речи – ТРИЗ - технология консультация 119
Радіоприймальні пристрої ЗРЛ. Загальні відомості про радіоприймальні пристрої. (Тема 4.1) Радіоприймальні пристрої ЗРЛ. Загальні відомості про радіоприймальні пристрої. (Тема 4.1) 109
Презентація до уроку української літератури на тему: Проблема добра і зла в творчості Івана Нечуя-Левицького та Панаса Мирного (10 клас) Презентація до уроку української літератури на тему: Проблема добра і зла в творчості Івана Нечуя-Левицького та Панаса Мирного (10 клас) 137
Общие положения инновационного менеджмента Общие положения инновационного менеджмента 85
История празднования Рождества на Руси История празднования Рождества на Руси 99
Портфоліо Бондарчук Катерини Портфоліо Бондарчук Катерини 101
Субъект РФ.Ставропольский край Субъект РФ.Ставропольский край 114
Новогодняя сказка презентация для интерактивной доски Новогодняя сказка презентация для интерактивной доски 117
Развитие мотивации учебной деятельности младших школьников материал по теме Развитие мотивации учебной деятельности младших школьников материал по теме 114
с/р игра магазин презентация к уроку (младшая группа) с/р игра магазин презентация к уроку (младшая группа) 150
Иммунитет противовирусный Иммунитет противовирусный 103
Школьный двор - территория радости Школьный двор - территория радости 142
ОБЩИЙ ВАРИАБЕЛЬНЫЙ ИММУНОДЕФИЦИТ ОБЩИЙ ВАРИАБЕЛЬНЫЙ ИММУНОДЕФИЦИТ 129