- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Построение линии пересечения поверхности проецирующей плоскостью
Содержание
- 2. Пересечение многогранника проецирующей плоскостью Линия пересечения
- 3. Пересечение пирамиды проецирующей плоскостьюЗадача. Построить линию пересечения пирамиды горизонтально проецирующей плоскостью Г.
- 4. Построение горизонтальной проекции (k1) линии пересечения пирамиды
- 5. Построение фронтальной проекции (k2) линии пересечения пирамиды
- 6. Пересечение многогранника проецирующими плоскостямиПри пересечении многогранника несколькими
- 7. Пересечение призмы проецирующими плоскостямиЗадача. Построить линию пересечения призмы проецирующими плоскостями.Обозначаем рёбра призмы и секущие плоскости.
- 8. Построение фронтальной проекции линии пересечения призмы проецирующими
- 9. Построение горизонтальной и профильной проекций линии пересечения
- 10. Пересечение многогранника проецирующими плоскостямиСоединив найденные проекции точек
- 11. Пересечение поверхности вращения проецирующей плоскостьюЛиния пересечения поверхности
- 12. Пересечение поверхности цилиндра проецирующими плоскостямиСекущая плоскость перпендикулярна оси вращения цилиндра. Линия пересечения –окружность.
- 13. Сечение цилиндраСекущая плоскость не перпендикулярна оси вращения цилиндра. Линия пересечения –эллипс.
- 14. Сечение цилиндраСекущая плоскость параллельна оси вращения цилиндра.
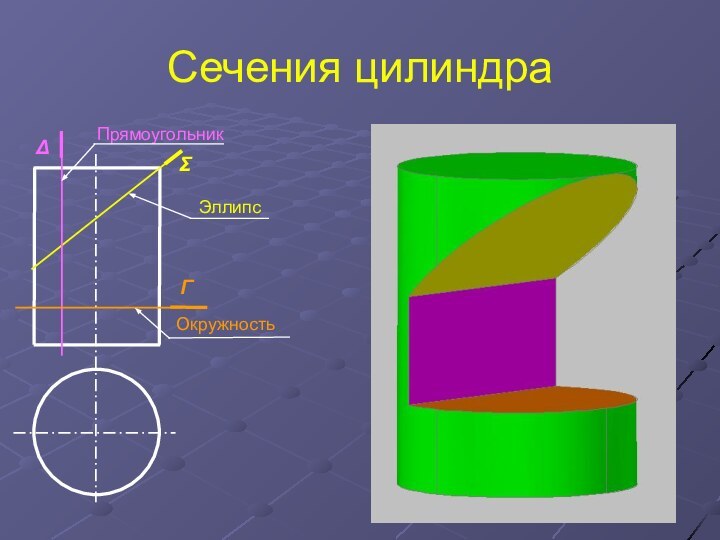
- 15. Сечения цилиндраПрямоугольникЭллипсОкружностьГΔΣ
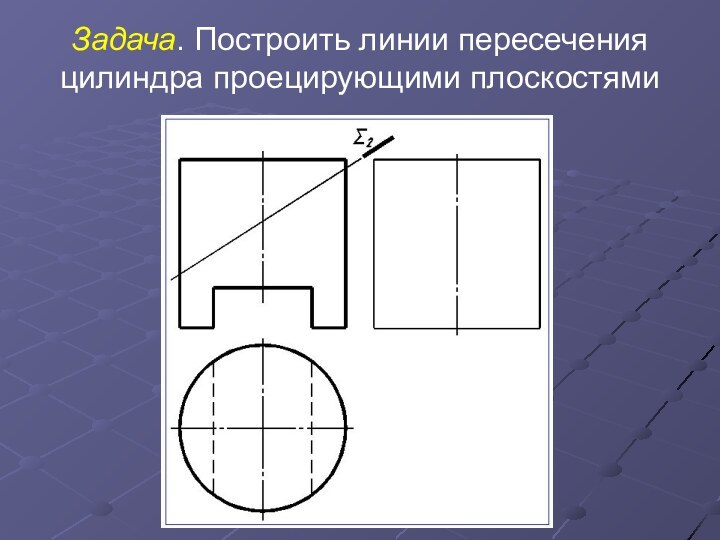
- 16. Задача. Построить линии пересечения цилиндра проецирующими плоскостями
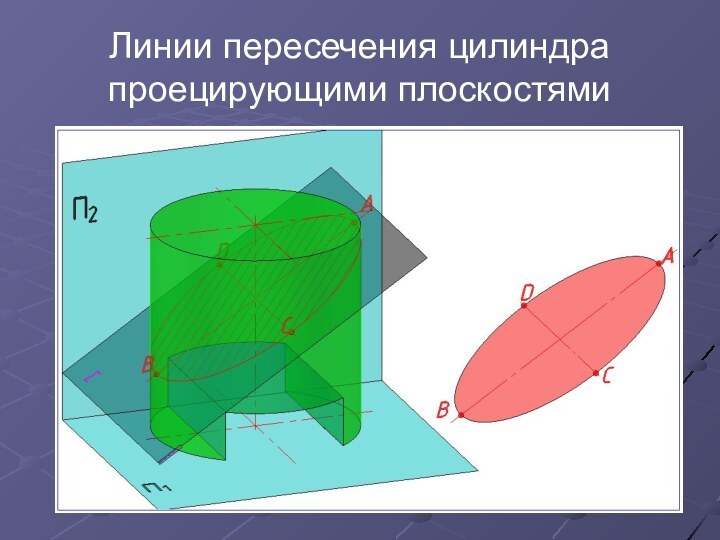
- 17. Линии пересечения цилиндра проецирующими плоскостями
- 18. Построение линии k пересечения цилиндра фронтально проецирующей
- 19. Построение линии k пересечения цилиндра фронтально проецирующей
- 20. Построение выреза, образованного плоскостями уровняПлоскости Δ, Г,
- 21. Построение выреза, образованного плоскостями уровняНа профильной проекции
- 22. Конические сеченияПлоскость Σ пересекает все образующие конуса.
- 23. Конические сеченияПлоскость Δ параллельна одной образующей конуса m(S1). Линия сечения – парабола.
- 24. Конические сеченияПлоскость Г проходит через вершину конуса
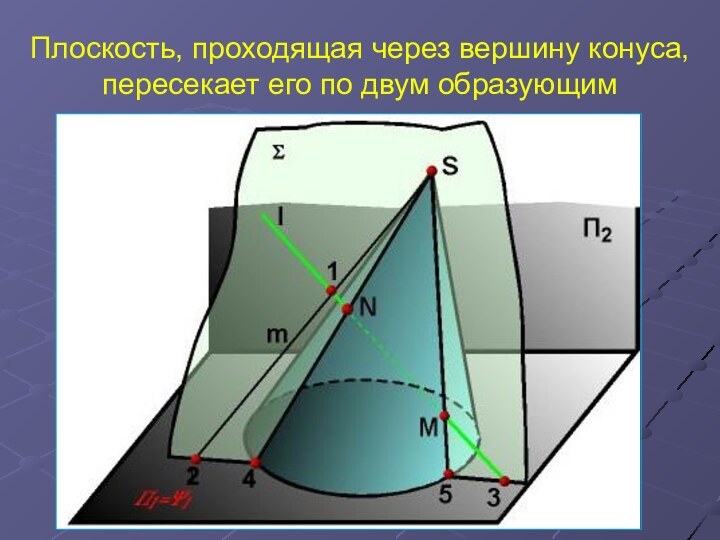
- 25. Плоскость, проходящая через вершину конуса, пересекает его по двум образующим
- 26. Конус с вырезомПостроить линии пересечения конуса проецирующими
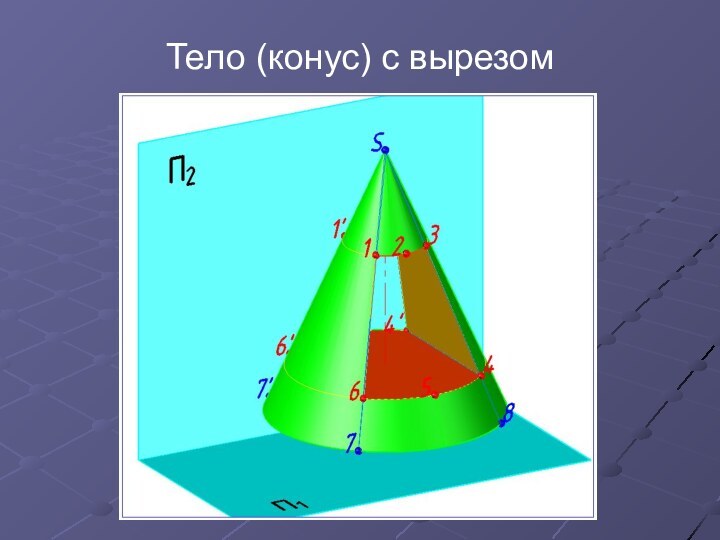
- 27. Тело (конус) с вырезом
- 28. Конус с вырезомПлоскости Ф и Σ проходят
- 29. Конус с вырезомВычерчиваем горизонтальные проекции образующих (S-7, S-7′, S-8, S-8′) и окружностей (m и m′).
- 30. Конус с вырезомПо линиям связи по принадлежности
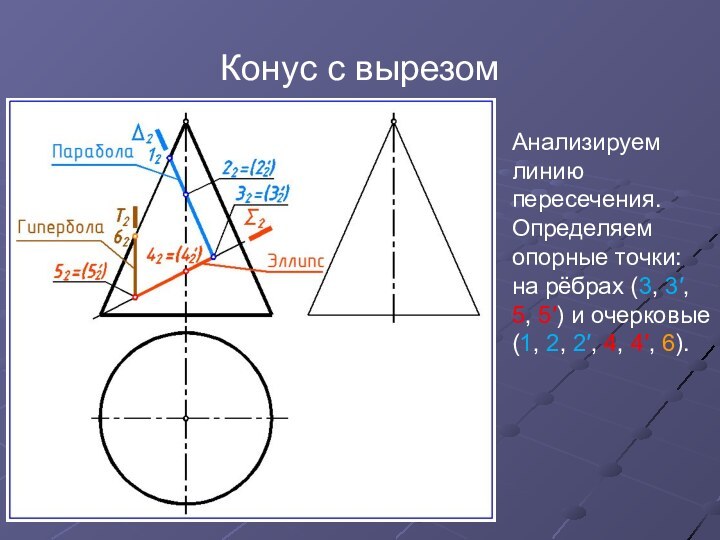
- 31. Конус с вырезомПостроить линии пересечения конуса проецирующими
- 32. Конус с вырезомАнализируем линию пересечения.Определяем опорные точки:
- 33. Конус с вырезом
- 34. Конус с вырезом
- 35. Конус с вырезом
- 36. Конус с вырезом
- 37. Скачать презентацию
- 38. Похожие презентации
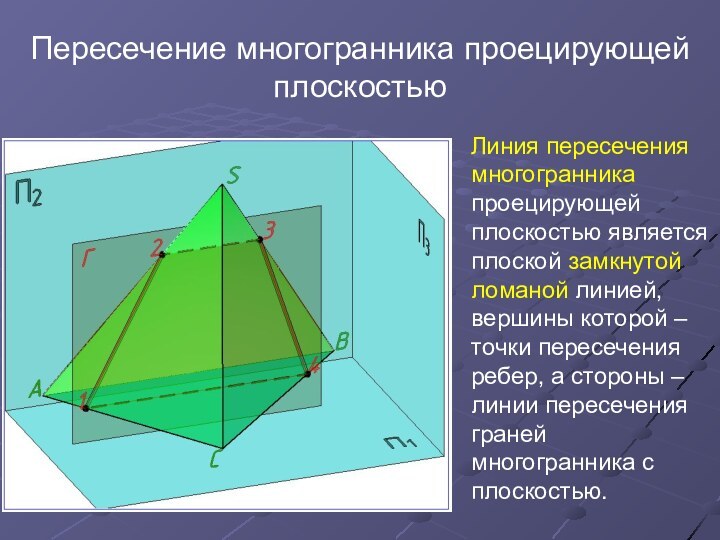
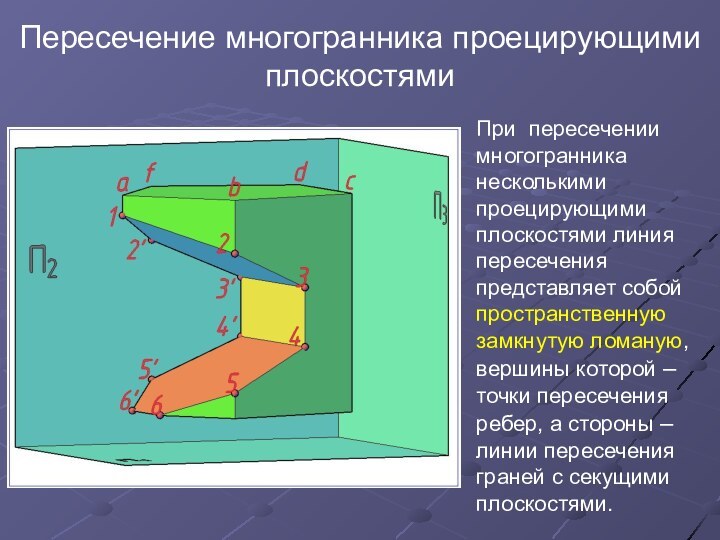
Пересечение многогранника проецирующей плоскостью Линия пересечения многогранника проецирующей плоскостью является плоской замкнутой ломаной линией, вершины которой – точки пересечения ребер, а стороны – линии пересечения граней многогранника с плоскостью.
Слайд 3
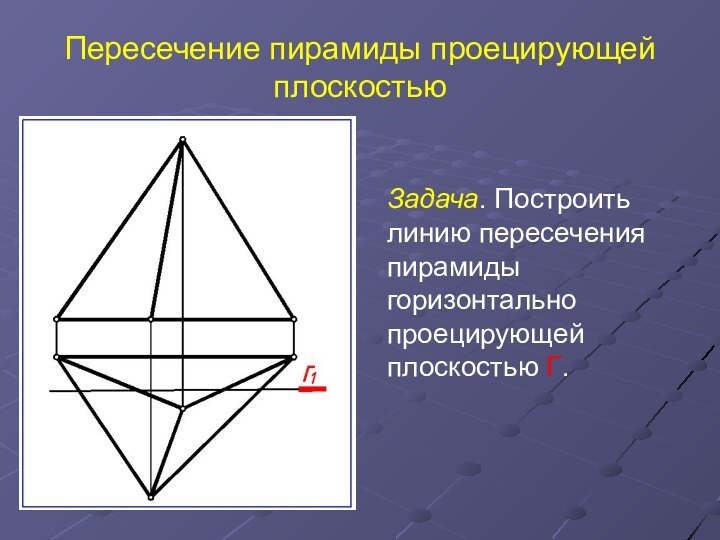
Пересечение пирамиды проецирующей плоскостью
Задача. Построить линию пересечения пирамиды
горизонтально проецирующей
плоскостью Г.
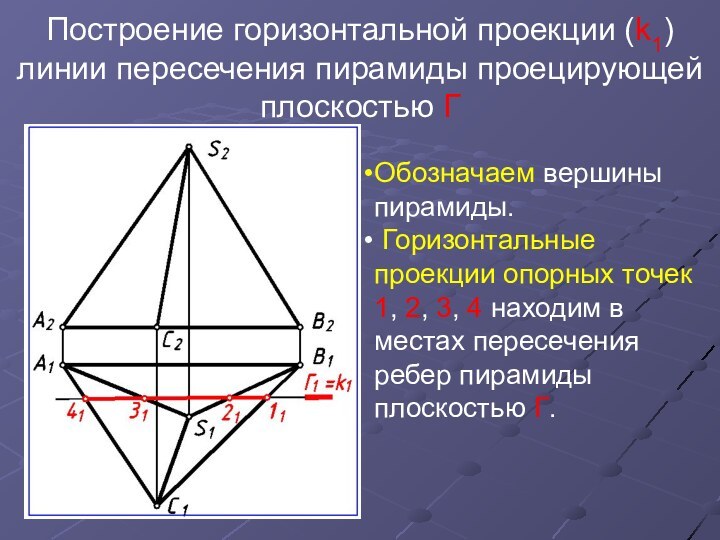
Слайд 4 Построение горизонтальной проекции (k1) линии пересечения пирамиды проецирующей
плоскостью Г
Обозначаем вершины пирамиды.
Горизонтальные проекции опорных точек 1,
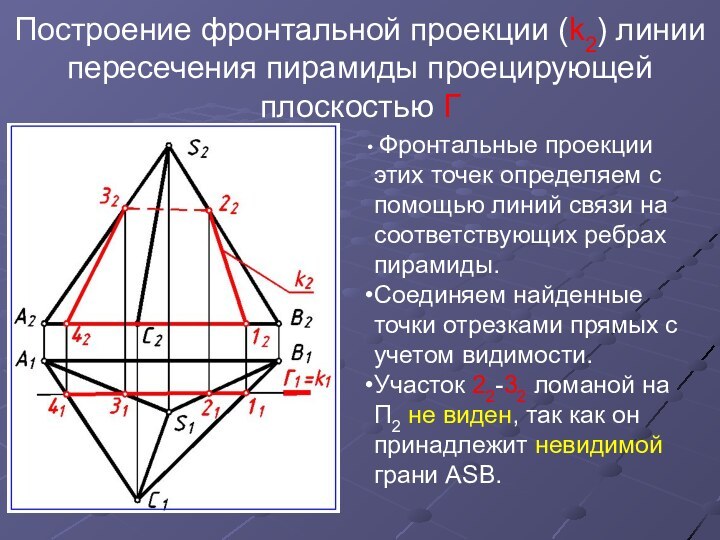
2, 3, 4 находим в местах пересечения ребер пирамиды плоскостью Г.Слайд 5 Построение фронтальной проекции (k2) линии пересечения пирамиды проецирующей
плоскостью Г
Фронтальные проекции этих точек определяем с помощью
линий связи на соответствующих ребрах пирамиды.Соединяем найденные точки отрезками прямых с учетом видимости.
Участок 22-32 ломаной на П2 не виден, так как он принадлежит невидимой грани АSВ.
Слайд 6
Пересечение многогранника проецирующими плоскостями
При пересечении многогранника несколькими проецирующими
плоскостями линия пересечения представляет собой пространственную замкнутую ломаную, вершины
которой – точки пересечения ребер, а стороны – линии пересечения граней с секущими плоскостями.
Слайд 7
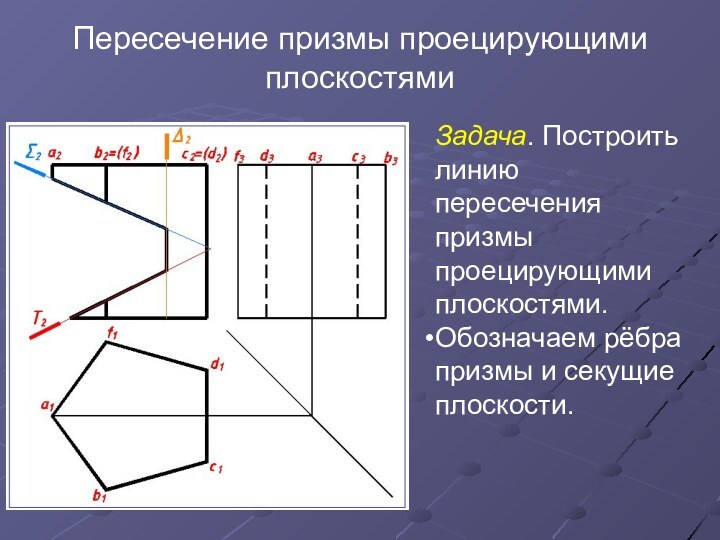
Пересечение призмы проецирующими плоскостями
Задача. Построить линию пересечения призмы
проецирующими плоскостями.
Обозначаем рёбра призмы и секущие плоскости.
Слайд 8
Построение фронтальной проекции линии пересечения призмы проецирующими плоскостями
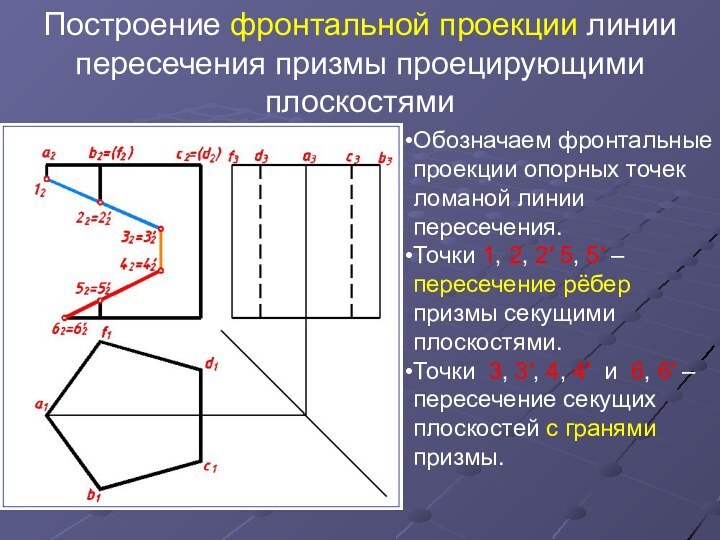
Обозначаем
фронтальные проекции опорных точек ломаной линии пересечения.
Точки 1,
2, 2′ 5, 5′ – пересечение рёбер призмы секущими плоскостями. Точки 3, 3′, 4, 4′ и 6, 6′ – пересечение секущих плоскостей с гранями призмы.
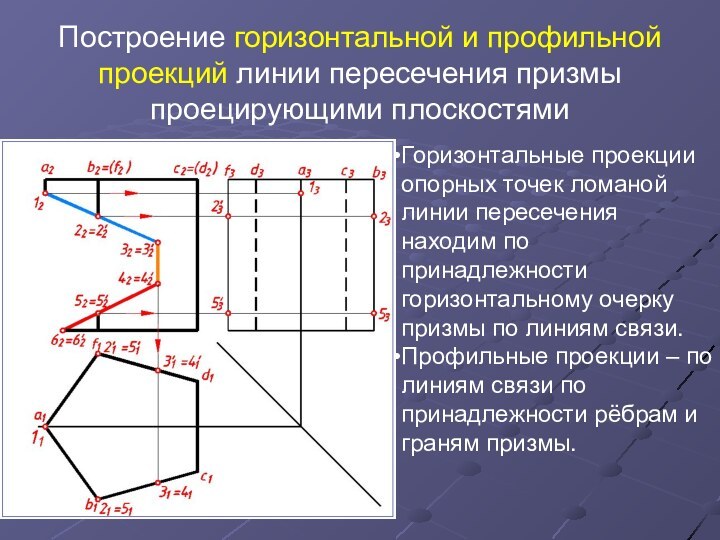
Слайд 9 Построение горизонтальной и профильной проекций линии пересечения призмы
проецирующими плоскостями
Горизонтальные проекции опорных точек ломаной линии пересечения находим
по принадлежности горизонтальному очерку призмы по линиям связи.Профильные проекции – по линиям связи по принадлежности рёбрам и граням призмы.
Слайд 10
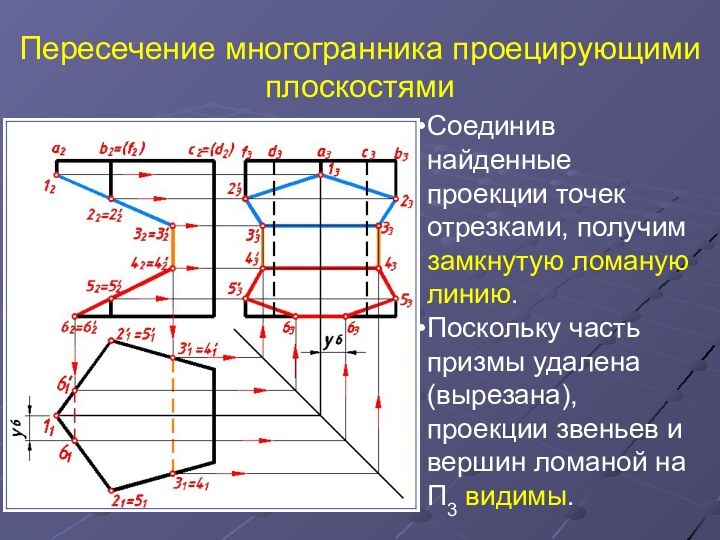
Пересечение многогранника проецирующими плоскостями
Соединив найденные проекции точек отрезками,
получим замкнутую ломаную линию.
Поскольку часть призмы удалена (вырезана), проекции
звеньев и вершин ломаной на П3 видимы.
Слайд 11
Пересечение поверхности вращения проецирующей плоскостью
Линия пересечения поверхности вращения
проецирующей плоскостью представляет собой плоскую замкнутую кривую.
Для построения этой
кривой определяем точки пересечения ряда образующих поверхности с секущей плоскостью. В первую очередь определяем опорные точки.К опорным точкам линии относятся: экстремальные (высшая, низшая, ближняя, дальняя, левая, правая), и очерковые. В рассматриваемых задачах очерковые точки одновременно являются точками смены видимости.
Слайд 12
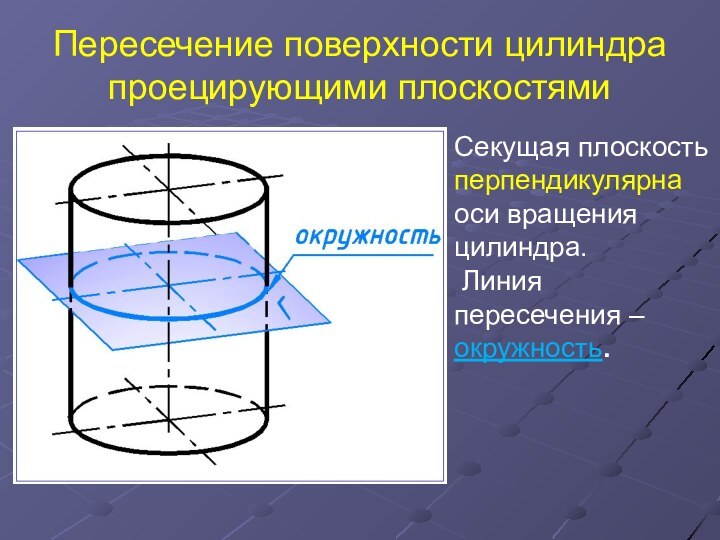
Пересечение поверхности цилиндра проецирующими плоскостями
Секущая плоскость перпендикулярна оси
вращения цилиндра.
Линия пересечения –окружность.
Слайд 13
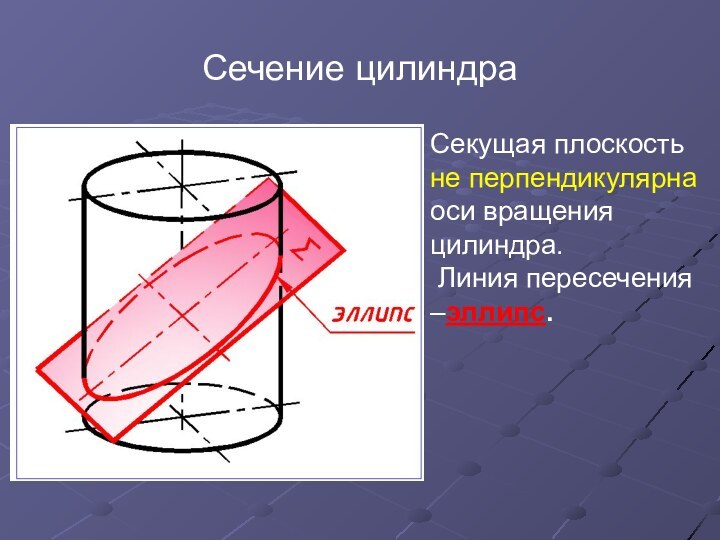
Сечение цилиндра
Секущая плоскость не перпендикулярна оси вращения цилиндра.
Линия пересечения –эллипс.
Слайд 14
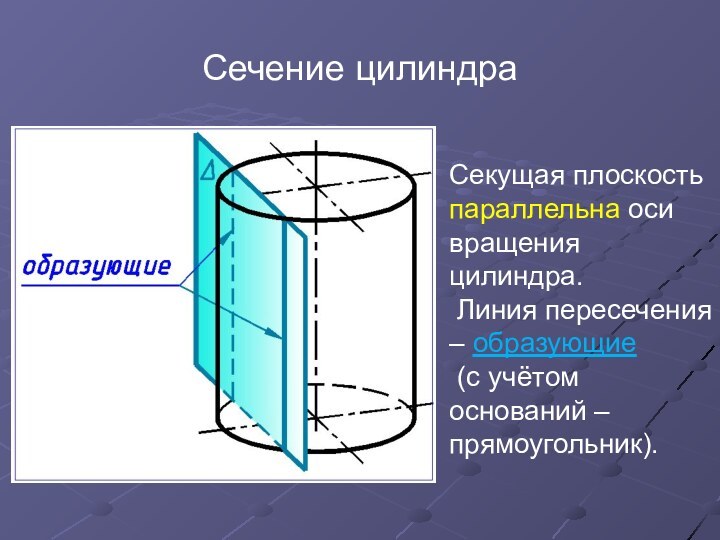
Сечение цилиндра
Секущая плоскость параллельна оси вращения цилиндра.
Линия
пересечения – образующие
(с учётом оснований – прямоугольник).
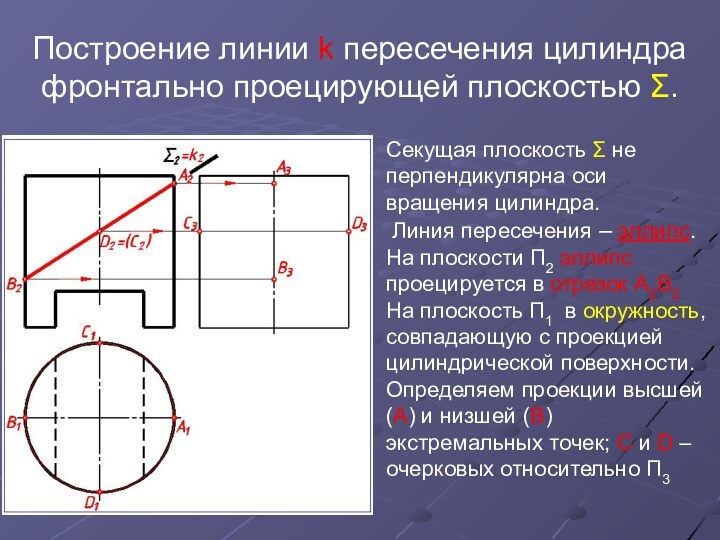
Слайд 18 Построение линии k пересечения цилиндра фронтально проецирующей плоскостью
Σ.
Секущая плоскость Σ не перпендикулярна оси вращения цилиндра.
Линия
пересечения – эллипс.На плоскости П2 эллипс проецируется в отрезок А2В2
На плоскость П1 в окружность, совпадающую с проекцией цилиндрической поверхности. Определяем проекции высшей (А) и низшей (В) экстремальных точек; С и D – очерковых относительно П3
Слайд 19 Построение линии k пересечения цилиндра фронтально проецирующей плоскостью
Σ.
Линия пересечения на плоскость П3 проецируется в эллипс.
Профильные проекции
точек, принадлежащих эллипсу, строим по двум известным (горизонтальной и фронтальной). Соединив полученные точки плавной кривой с учетом видимости, получим эллипс, являющийся профильной проекцией фигуры сечения. Точки С и D являются точками смены видимости на П3.
Слайд 20
Построение выреза, образованного плоскостями уровня
Плоскости Δ, Г, Δ′
образуют вырез, ограниченный двумя прямоугольниками (3, 4, 4′, 3′,
3) и (6, 7, 6′, 7′, 6); двумя частями окружности (4, 5, 6) и (4′, 5′, 6′).Горизонтальные проекции линий выреза расположены на окружности, в которую проецируется цилиндр.
Профильные проекции точек 5 и 5 ′находим по линиям связи на очерке, остальные – по координатам «y».
Слайд 21
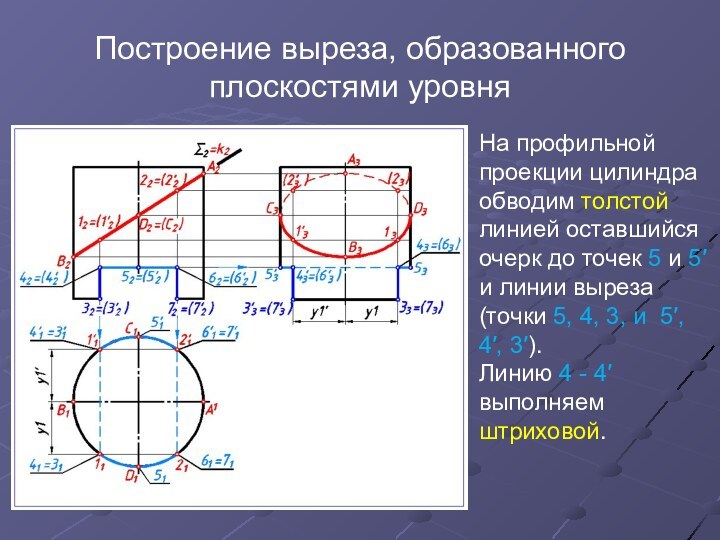
Построение выреза, образованного плоскостями уровня
На профильной проекции цилиндра
обводим толстой линией оставшийся очерк до точек 5 и
5′ и линии выреза (точки 5, 4, 3, и 5′, 4′, 3′).Линию 4 - 4′ выполняем штриховой.
Слайд 22
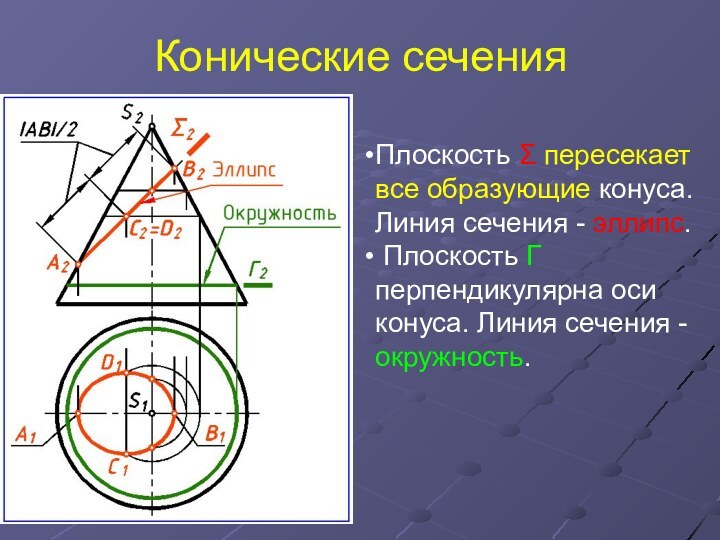
Конические сечения
Плоскость Σ пересекает все образующие конуса.
Линия
сечения - эллипс.
Плоскость Г перпендикулярна оси конуса. Линия
сечения - окружность.
Слайд 23
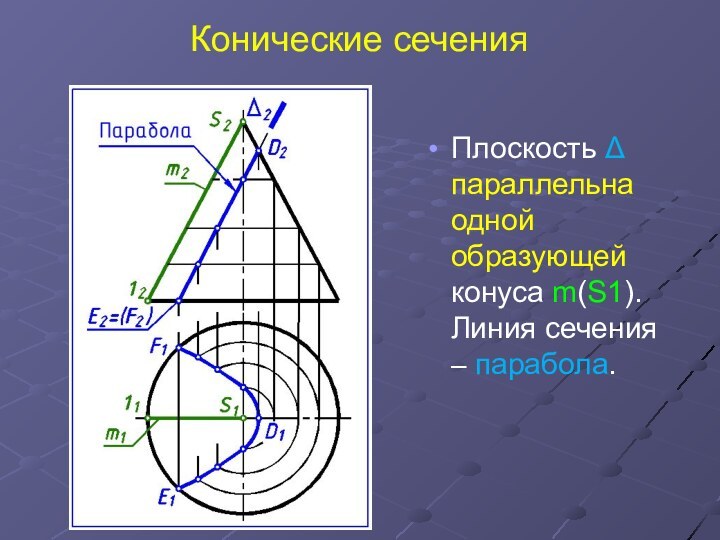
Конические сечения
Плоскость Δ параллельна одной образующей конуса m(S1).
Линия сечения – парабола.
Слайд 24
Конические сечения
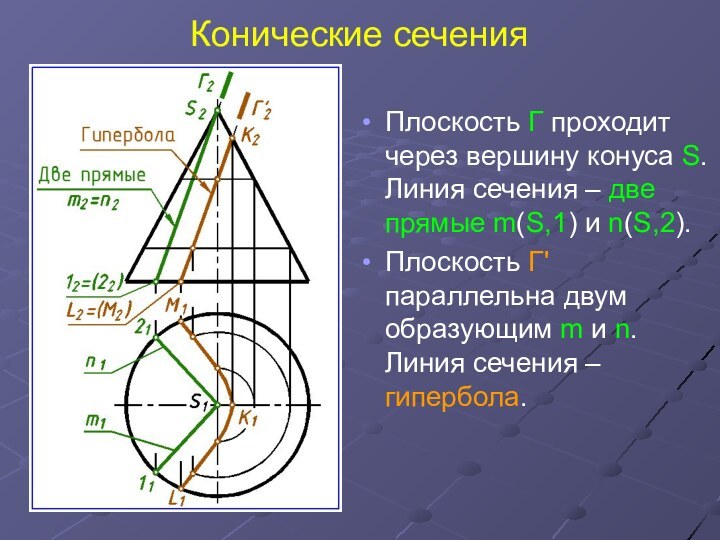
Плоскость Г проходит через вершину конуса S.
Линия сечения – две прямые m(S,1) и n(S,2).
Плоскость
Г' параллельна двум образующим m и n. Линия сечения – гипербола.
Слайд 26
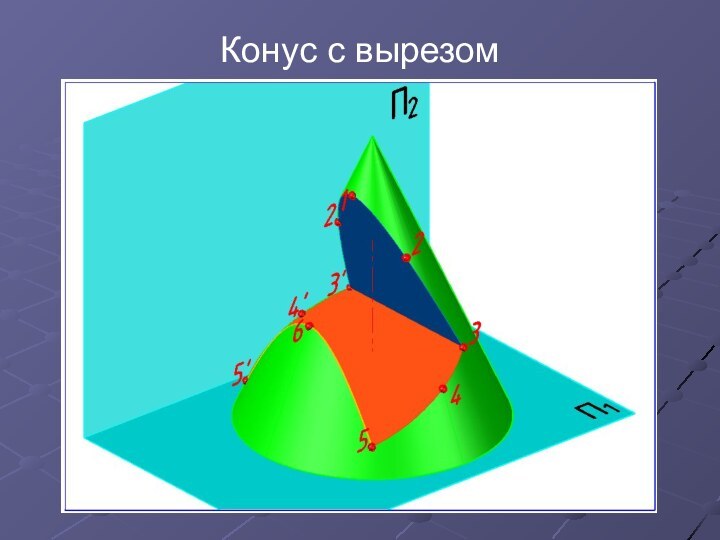
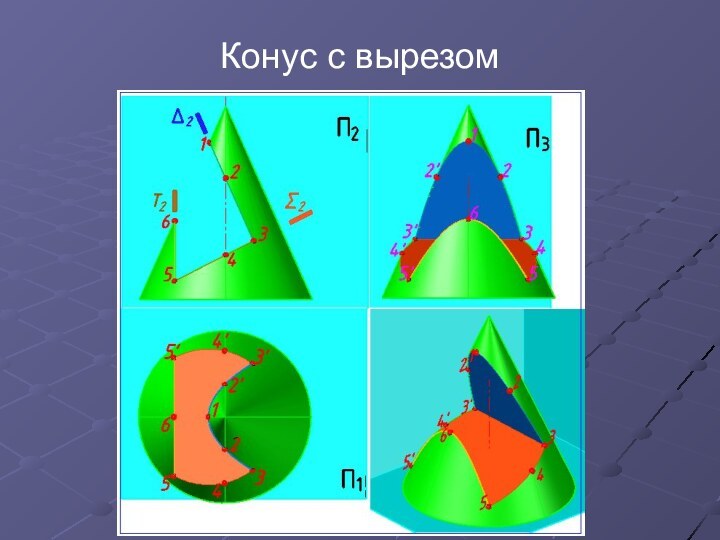
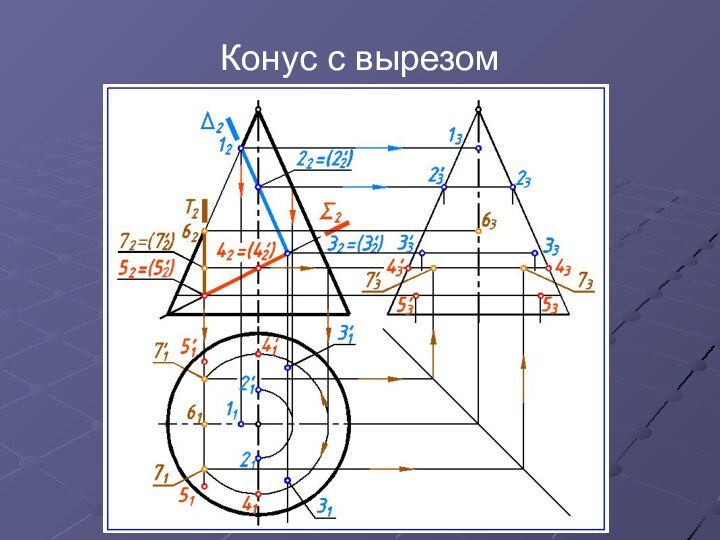
Конус с вырезом
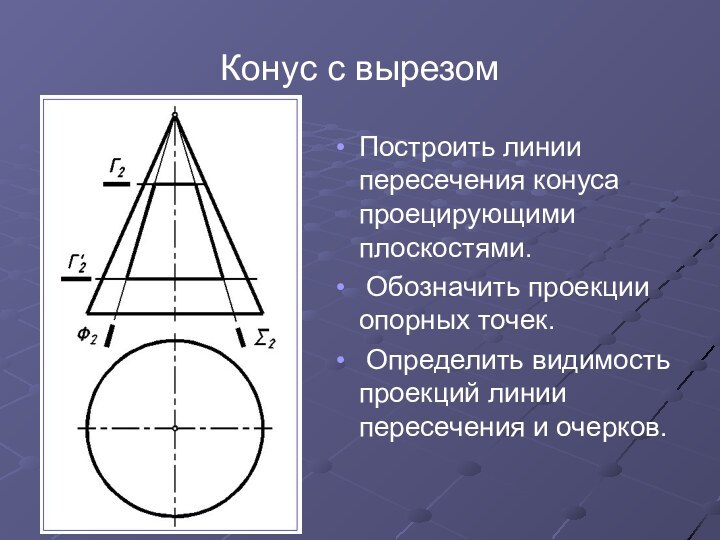
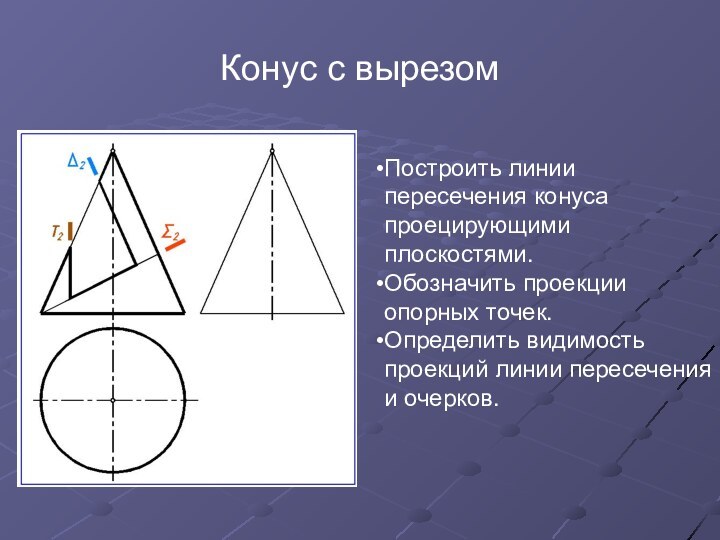
Построить линии пересечения конуса проецирующими плоскостями.
Обозначить проекции опорных точек.
Определить видимость проекций линии пересечения
и очерков.
Слайд 28
Конус с вырезом
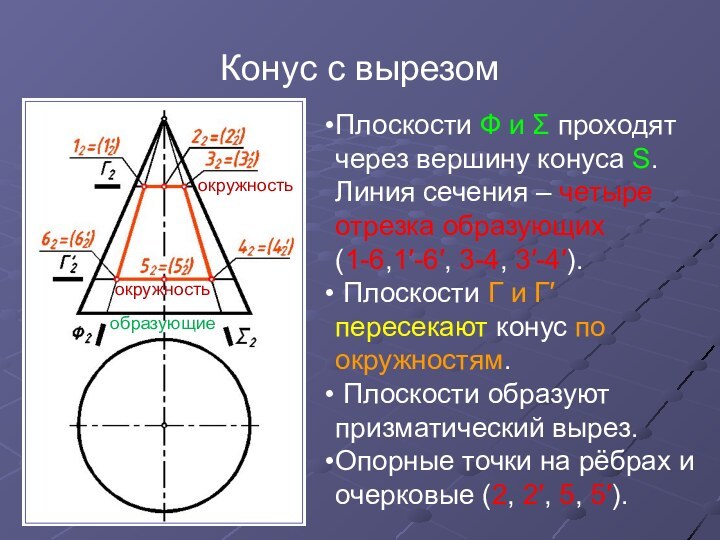
Плоскости Ф и Σ проходят через
вершину конуса S. Линия сечения – четыре отрезка образующих (1-6,1′-6′,
3-4, 3′-4′).Плоскости Г и Г′ пересекают конус по окружностям.
Плоскости образуют призматический вырез.
Опорные точки на рёбрах и очерковые (2, 2′, 5, 5′).
окружность
окружность
образующие
Слайд 29
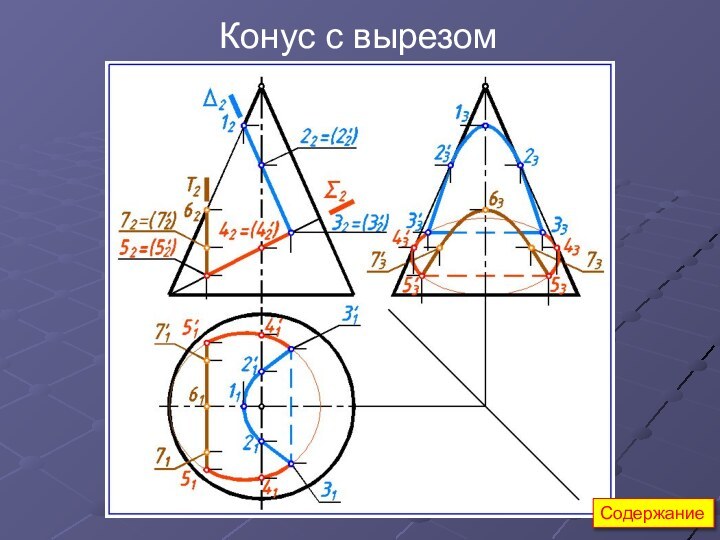
Конус с вырезом
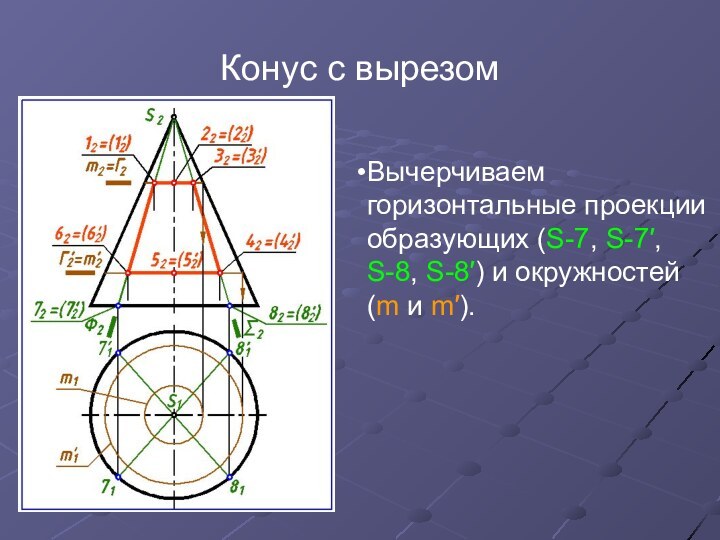
Вычерчиваем горизонтальные проекции образующих (S-7, S-7′,
S-8,
S-8′) и окружностей (m и m′).
Слайд 30
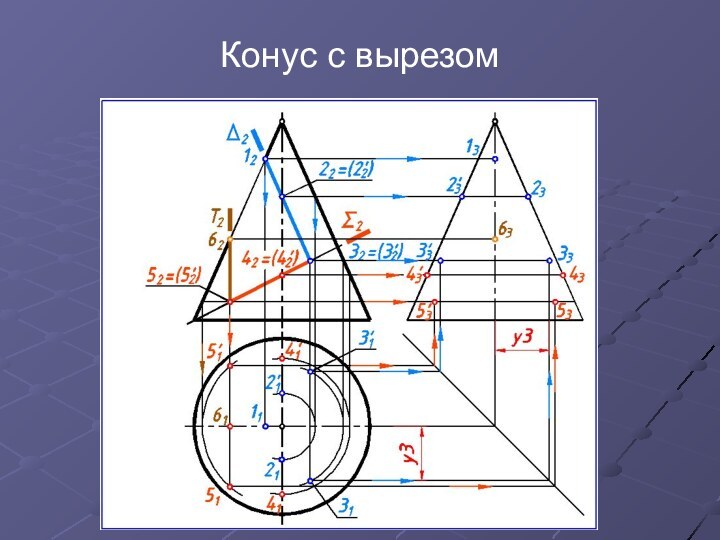
Конус с вырезом
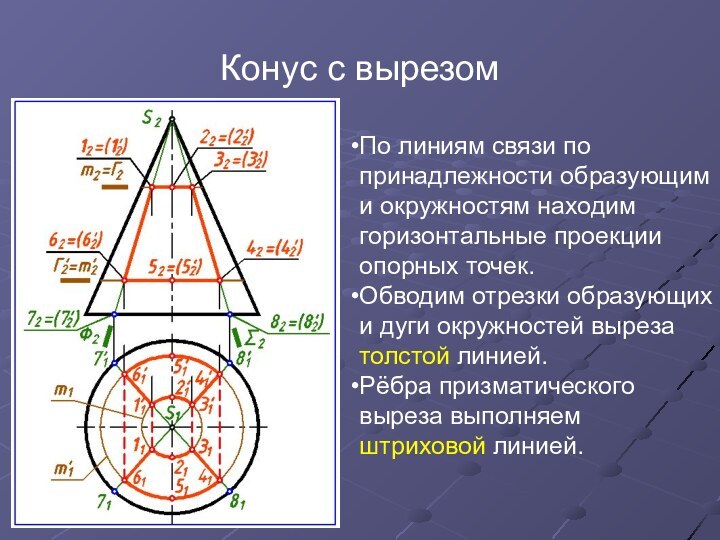
По линиям связи по принадлежности образующим
и окружностям находим горизонтальные проекции опорных точек.
Обводим отрезки образующих
и дуги окружностей выреза толстой линией.Рёбра призматического выреза выполняем штриховой линией.
Слайд 31
Конус с вырезом
Построить линии пересечения конуса проецирующими плоскостями.
Обозначить
проекции опорных точек.
Определить видимость проекций линии пересечения и очерков.
Слайд 32
Конус с вырезом
Анализируем линию пересечения.
Определяем опорные точки: на
