Слайд 2
Тема лекции:
Проверка статистических гипотез. Критерии согласия.
Слайд 3
Проверка статистических гипотез.
Слайд 4
Проверка статистических гипотез.
Статистической гипотезой называется всякое непротиворечивое множество
утверждений {Н0, Н1, … , Hk-1} относительно свойств распределения
случайной величины.
Любое из утверждений Hi называется альтернативой гипотезы.
Простейшей гипотезой является двухальтернативная:
{H0, H1}. В этом случае альтернативу H0 называют нулевой гипотезой, а H1-конкурирующей гипотезой.
Слайд 5
Проверка статистических гипотез.
Критерием называется случайная величина
U =ϕ
( x1,K , xn ) ,где xi –значения выборки,
которая позволяет принять или отклонить нулевую гипотезу
H0.
Значения критерия, при которых гипотеза H0 отвергается, образуют критическую область проверяемой гипотезы, а значения критерия, при которых гипотезу принимают, область принятия гипотезы (область допустимых значений).
Критические точки отделяют критическую область от области принятия гипотезы.
Слайд 6
Ошибка первого и
второго рода.
Слайд 7
Ошибка первого и второго рода.
Ошибка первого рода состоит
в том, что будет отклонена гипотеза H0,если она верна
("пропуск цели").
Вероятность совершить ошибку первого рода
обозначается α и называется уровнем значимости.
Наиболее часто на практике принимают,
что α = 0,05 или α = 0,01.
Слайд 8
Ошибка первого и второго рода.
Ошибка второго рода заключается
в том, что гипотеза H0 принимается,если она неверна
("ложное срабатывание").
Вероятность ошибки этого рода обозначается β. Вероятность не допустить ошибку второго рода (1-β) называют мощностью критерия.
Слайд 9
Проверка гипотезы о равенстве вероятностей
Слайд 10
Проверка гипотезы о равенстве вероятностей
Пусть произведено две серии
опытов, состоящих соответственно из n1 и n2 опытов. В
каждом из них регистрировалось появление одного и того же события А.
В первой серии событие А появилось в k1 опытах, во второй – в k2 опытах, причем частота события А в первой серии получилась больше, чем во второй:
Слайд 11
Проверка гипотезы о равенстве вероятностей
Разность между двумя частота
получилась равной
Спрашивается, значимо или не значимо это расхождение?
Указывает ли оно на то, что в первой серии опытов событие A действительно вероятнее, чем во второй, или расхождение между частотами надо считать случайным?
Слайд 12
Двухальтернативная гипотеза
Выдвинем двухальтернативную гипотезу {H0, H1}.
Пусть H0 –
различия в вероятностях не существует, т.е. обе серии опытов
произведены в одинаковых условиях, а расхождение U объясняется случайными причинами,
H1 – различие в вероятностях существует, т.е. обе серии опытов произведены не в одинаковых условиях.
Слайд 13
Двухальтернативная гипотеза
В данном случае нуль-гипотеза H0 состоит в
том, что обе серии опытов однородны и что вероятность
р появления события А в них одна и та же, приближенно равная частоте, которая получится, если обе серии смешать в одну:
Слайд 14
Двухальтернативная гипотеза
При достаточно больших n1 и n2 каждая
из случайных величин p1* и p2* распределена практически нормально,
с одним и тем же математическим ожиданием m= p ≈ p* .
Слайд 15
Двухальтернативная гипотеза
Что касается дисперсий D1 и D2 в
первой и во второй сериях, то они различны и
равны соответственно
Слайд 16
Двухальтернативная гипотеза
В качестве критерия будем использовать случайную величину
U =p1*- p2* , которая также имеет приближенно нормальное
распределение
с математическим ожиданием
mu =0 и дисперсией
откуда
Слайд 17
Двухальтернативная гипотеза
Определим критическую точку Uα для заданного уровня
значимости α из уравнения:
Если значение, вычисленное по формуле разности
двух частот, больше, чем критическое
значение, т.е. U > Uα, то гипотеза H0 отклоняется, в противном случае нет
оснований ее отклонить.
Слайд 19
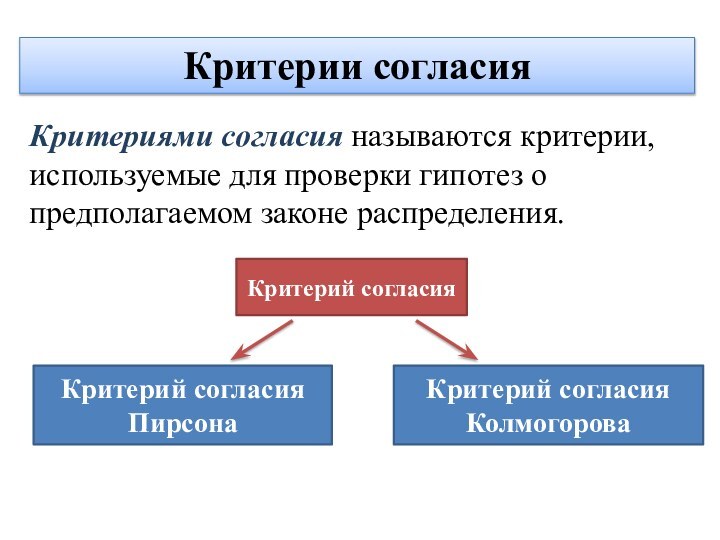
Критерии согласия
Критериями согласия называются критерии, используемые для проверки
гипотез о предполагаемом законе распределения.
Критерий согласия
Критерий согласия Пирсона
Критерий
согласия Колмогорова
Слайд 20
Критерий согласия
Пирсона ( χ2 )
Слайд 21
Алгоритм проверки критерия согласия Пирсона
1. Построить интервальный
статистический ряд и гистограмму.
2. По виду гистограммы выдвинуть гипотезу:
H0
– величина X распределена по такому-то закону: f(x) = f0(x),
H1 – величина X не распределена по такому-то закону:
f(x) ≠ f0(x),
где f0(x), F0(x) – плотность и функция гипотетического закона распределения
Слайд 22
Алгоритм проверки критерия согласия Пирсона
3. Используя метод
моментов или максимального правдоподобия, определить оценки неизвестных параметров
гипотетического закона распределения.
4. Вычислить значение критерия по формуле
где pj – теоретическая вероятность попадания случайной величины в j- й интервал.
Слайд 23
Алгоритм проверки критерия согласия Пирсона
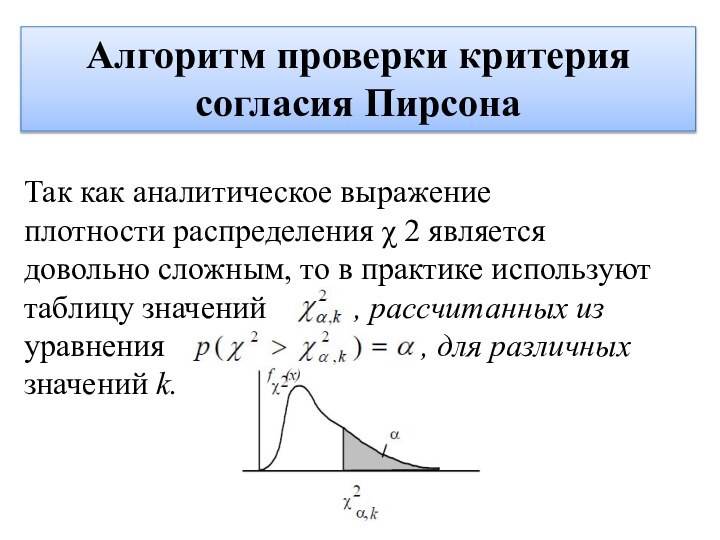
Так как аналитическое
выражение
плотности распределения χ 2 является
довольно сложным, то в практике
используют
таблицу значений , рассчитанных из
уравнения , для различных
значений k.
Слайд 24
Алгоритм проверки критерия согласия Пирсона
5. Из таблицы
распределения χ 2 выбирается значение ,где
α –заданный уровень значимости (α = 0,05 или α = 0,01), а k – число степеней свободы, которое определяется по формуле
k = M - 1 - s.
Здесь s – число неизвестных параметров гипотетического закона распределения, значения которых были определены в п. 3.
Слайд 25
Алгоритм проверки критерия согласия Пирсона
6. Если
значение, вычисленное по формуле χ 2 , больше,
чем критическое значение,
т.е. , то гипотеза H0 отклоняется, в противном случае нет оснований ее отклонить
Слайд 27
Алгоритм проверки
критерия согласия Колмогорова
1. Построить вариационный ряд
и график эмпирической функции
распределения F*(x).
2. По виду графика F*(x)
выдвинуть гипотезу:
H0 : F(x) = F0(x),
H1 : F(x) ≠ F0(x),
где F0(x) – функция гипотетического закона распределения.
Слайд 28
Алгоритм проверки
критерия согласия Колмогорова
3. Используя метод моментов
или максимального правдоподобия
определить оценки неизвестных параметров
гипотетического закона распределения.
4. Рассчитать 10...20 значений функции F0(x) и построить ее график в одной системе координат с функцией F*(x).
Слайд 29
Алгоритм проверки
критерия согласия Колмогорова
5. По графику определить
максимальное по модулю отклонение между функциями F*(x) и F0(x).
Слайд 30
Алгоритм проверки
критерия согласия Колмогорова
6. Вычислить значение критерия
Колмогорова
7. Величина λ распределена по закону Колмогорова, который не
зависит от закона распределения величины X,:
Слайд 31
Алгоритм проверки
критерия согласия Колмогорова
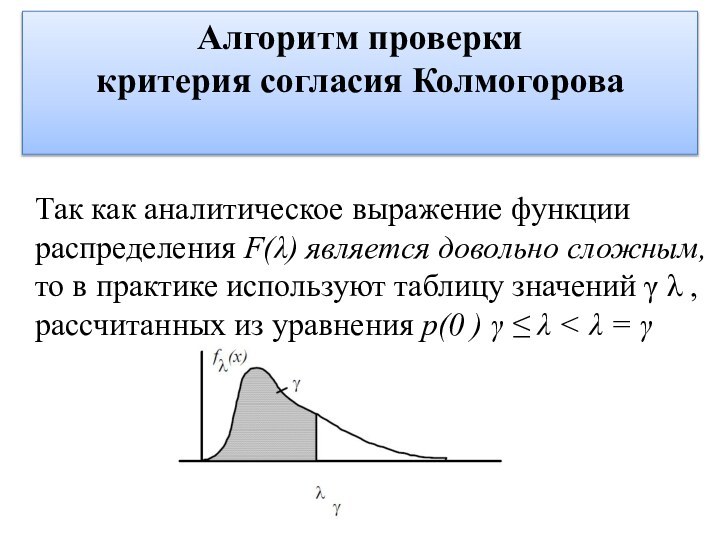
Так как аналитическое выражение
функции
распределения F(λ) является довольно сложным,
то в практике используют таблицу
значений γ λ ,
рассчитанных из уравнения p(0 ) γ ≤ λ < λ = γ
Слайд 32
Алгоритм проверки
критерия согласия Колмогорова
7. Из таблицы распределения
Колмогорова
выбрать критическое значение γ λ , γ =1−α .α
–
заданный уровень значимости
(α = 0,05 или α = 0,01).
8. Если λ > λγ , то нулевая гипотеза H0 отклоняется, в противном случае нет оснований ее отклонить.
Слайд 33
Достоинства критерия согласия Колмогорова
Достоинствами критерия Колмогорова по сравнению
с критерием χ2:
Являются возможность его применения при очень маленьких
объемах выборки
(n < 20), более высокая "чувствительность", а следовательно, меньшая трудоемкость вычислений.
Слайд 34
Недостатки критерия согласия Колмогорова
Недостатком является то, что эмпирическая
функция
распределения F*(x) должна быть построена по несгруппированным выборочным данным,
что затруднительно при больших объемах выборки.
Кроме этого, следует отметить, что критерий можно применять только в случае, когда известен не только вид функции распределения F0(x), но и все входящие в нее параметры