- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Правильные многогранники
Содержание
- 2. Определение: Многогранник-это часть пространства ограниченная совокупностью конечного
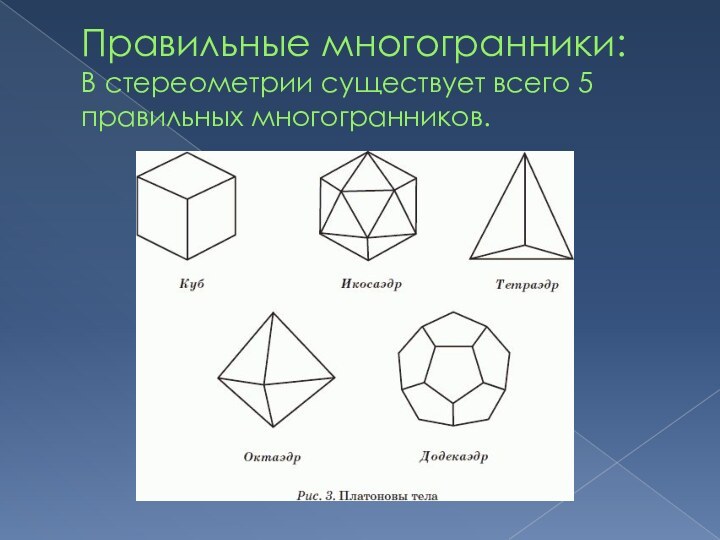
- 3. Правильные многогранники: В стереометрии существует всего 5 правильных многогранников.
- 4. Куб(гексаэдр) Составлен из шести квадратов. Каждая
- 5. Правильный икосаэдр Составлен из двадцати равносторонних треугольников.
- 6. Правильный тетраэдр Составлен из четырех равносторонних треугольников.
- 7. Правильный октаэдр Составлен из восьми равносторонних треугольников.
- 8. Правильный додекаэдр Составлен из двенадцати правильных пятиугольников.
- 9. История многогранников. Правильные многогранники известны с
- 10. Таэтет Афинский. его достижение — доказательство теоремы
- 11. Многогранники в жизни. 1. Многогранники в архитектуре.
- 12. 2.Многогранники в химии.
- 13. Многогранники в искусстве В эпоху Возрождения произошло
- 14. Скачать презентацию
- 15. Похожие презентации
Определение: Многогранник-это часть пространства ограниченная совокупностью конечного числа плоских многоугольников соединенных таким образом, что каждая сторона любого многогранника является стороной ровно одного многоугольника. Многоугольники называются гранями, их стороны - ребрами, а вершины – вершинами. Правильный многогранник-это












Слайд 2 Определение: Многогранник-это часть пространства ограниченная совокупностью конечного числа плоских
Слайд 4 Куб(гексаэдр) Составлен из шести квадратов. Каждая вершина куба
является вершиной трех квадратов. Следовательно плоских углов при каждой
вершине равна 270Слайд 5 Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина
икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов
при каждой вершине равна 300Слайд 6 Правильный тетраэдр Составлен из четырех равносторонних треугольников. Каждая вершина
тетраэдра является вершиной трех треугольников. Следовательно, сумма плоских углов
при каждой вершине равна 180Слайд 7 Правильный октаэдр Составлен из восьми равносторонних треугольников. Каждая вершина
октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов
при каждой вершине равна 240Слайд 8 Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина
додекаэдра является вершиной трех правильный пятиугольников Следовательно, сумма плоских
углов при каждой вершине равна 324
Слайд 9
История многогранников.
Правильные многогранники известны с древнейших времён. Их
орнаментные модели можно найти на резных каменных шарах, созданных
в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.





























