Слайд 2
Рекомендуемая литература
В.И. Нефёдов «Основы радиоэлектроники и связи», 2009
г
С.И. Баскаков «Радиотехнические цепи и сигналы», 2003 г.
С.И. Баскаков
«Радиотехнические цепи и сигналы.
Руководство к решению задач», 2002 г.
4. М.Т. Иванов, А.Б. Сергиенко, В.Н. Ушаков,
«Теоретические основы радиотехники», 2002 г.
5. М.П. Медиченко, В.П. Литвинов «Радиотехнические цепи и
сигналы, т.1; 2», 2011 г.
Слайд 3
Аппроксимация характеристик нелинейных элементов
Слайд 4
Аппроксимация характеристик нелинейных элементов
Известны и
используют следующие методы анализа нелиней-ных цепей при прохождении через
них детерминированных сигналов:
линеаризация характеристик нелинейного элемента (НЭ) при
фильтрации высших гармоник сигнала на выходе цепи;
аналитические, как правило, приближенные способы решения системы нелинейных уравнений, описывающих работу устройства;
спектральный, оценивающий нелинейные свойства цепи по спектру выходного сигнала;
численные способы решения системы нелинейных уравнений с
помощью компьютера;
Слайд 5
Аппроксимация характеристик нелинейных элементов
Наиболее часто
используют метод анализа нелинейных цепей, основанный на линеаризации характеристик
НЭ при фильтрации высших гармоник сигнала на выходе цепи.
Линеаризация (от лат. linearis – линейный) – метод приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяют анализом линейной системы, в некотором смысле эквивалент-ной исходной.
Слайд 6
Нелинейные элементы
В качестве примера нелинейных
цепей, точнее элементов, можно привести полупроводниковый выпрямительный диод, оставляющий
от синусоидального сигнала только однополярные (положительные или отрицательные) полусинусоиды, или трансформатор, насыщение сердечника которого магнитным полем приводит к «затуплению» вершин синусоиды (а с точки зрения частотного спектра, это сопровождается появлением гармоник основной частоты, а иногда и частот меньшей в кратное число раз основной частоты – субгармоник).
Слайд 7
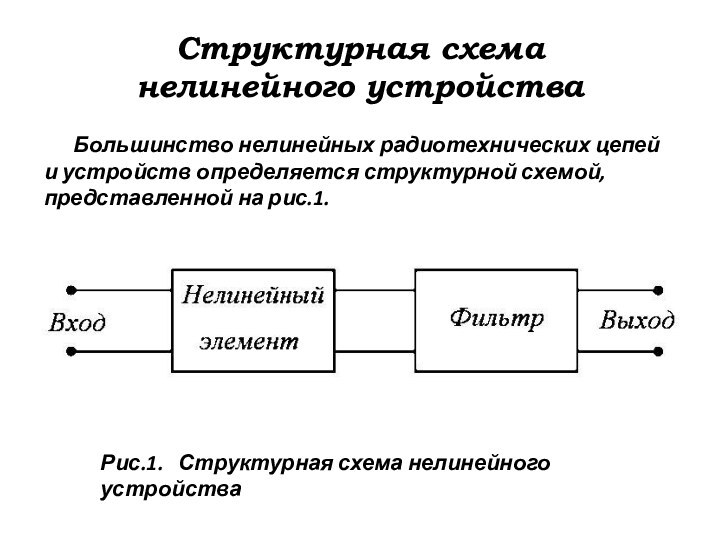
Структурная схема
нелинейного устройства
Большинство нелинейных
радиотехнических цепей
и устройств определяется структурной схемой, представленной на
рис.1.
Рис.1. Структурная схема нелинейного устройства
Слайд 8
Принцип работы нелинейного устройства
Согласно этой
схеме, входной сигнал непосредственно воздействует на нелинейный элемент, к
выходу которого подключён фильтр (линейная цепь). В этих случаях процесс в радиоэлектронной нелинейной цепи можно охарактеризовать двумя независимыми друг от друга операциями.
В результате первой операции в безынерционном нелинейном элементе происходит такое преобразование формы входного сигнала, при котором в его спектре появляются новые гармонические составляющие.
Слайд 9
Принцип работы нелинейного устройства
Вторую операцию
осуществляет фильтр, выделяющий нужные спектральные составляющие преобразованного входного сигнала.
Меняя параметры входных сигналов и используя различные нелинейные элементы и фильтры, можно осуществлять требуемую трансформацию спектра. К такой удобной теоретической модели сводятся многие схемы модуляторов, детекторов, автогенераторов, выпрямителей, умножителей, делителей и преобразователей частоты.
Слайд 10
Вольт-амперная характеристика нелинейного устройства
....................... (1)
Данное
соотношение аналитически может представлять собой обычную вольтамперную характеристику НЭ.
Слайд 11
Аппроксимация вольт-амперной характеристики
Слайд 12
Аппроксимация вольт-амперной характеристики
В радиотехнике и
теории передачи информации использу-ются несколько способов аппроксимации характеристик НЭ
– степеннáя, показательная, кусочно-линейная (линейно-ломаная). Наибольшее распространение получили аппроксимация степенным полиномом и кусочно-линейная аппроксимация сложных функций.
Слайд 13
Аппроксимация ВАХ
степенным полиномом
....... (2)
Постоянные коэффициенты ряда Тейлора
определяются формулой
............ (3)
Данный вид аппроксимации особенно
эффективен при малых амплитудах входных сигналов (как правило, доли вольта) в тех случаях, когда характеристика НЭ имеет вид гладкой кривой, т.е. кривая и её производные непрерывны и не имеют скачков.
Слайд 14
Аппроксимация ВАХ
степенным полиномом
Оптимальное число членов
ряда берётся в зависимости от тре-буемой точности аппроксимации. Чем
больше выбрано членов ряда, тем точнее аппроксимация. Аппроксимацию характеристик обычно удаётся достаточно точно осуществить полиномом не выше второй-третьей степени.
Слайд 15
Аппроксимация ВАХ
степенным полиномом
Слайд 16
Кусочно-линейная
аппроксимация ВАХ
Слайд 17
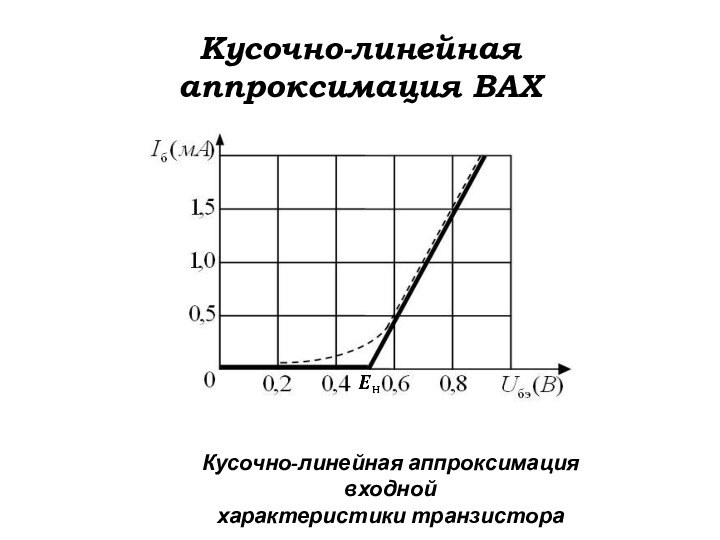
Кусочно-линейная
аппроксимация ВАХ
Кусочно-линейная аппроксимация входной
характеристики транзистора
Слайд 18
Кусочно-линейная аппроксимация входной ВАХ транзистора
В общем
случае дифференциальная крутизна характеристики
в рабочей точке определяется отношением
приращения тока
к приращению напряжения, и при малых их значениях имеем
............. (4)
Уравнение отрезка прямой при кусочно-линейной аппроксимации характеристики записывается в виде
.......... (5)
Чаще всего характеристику нелинейного элемента, к которому под-водится сигнал большой амплитуды, удаётся с приемлемой точно-стью аппроксимировать всего двумя отрезками прямых линий.
Слайд 19
Расчёт кусочно-линейной аппроксимации входной ВАХ транзистора
Тогда
крутизна ВАХ определится как
Слайд 20
Расчёт кусочно-линейной аппроксимации входной ВАХ транзистора
Слайд 21
Расчёт кусочно-линейной аппроксимации входной ВАХ транзистора
Повышение
точности аппроксимации характеристик нелинейных элементов достигается увеличением количества отрезков
линий. Однако это усложняет аналитическое выражение аппроксимирую-щей функции.
Слайд 22
Отклик нелинейной цепи на гармонический входной сигнал
Рис.3. Схема
цепи с нелинейным элементом
Слайд 23
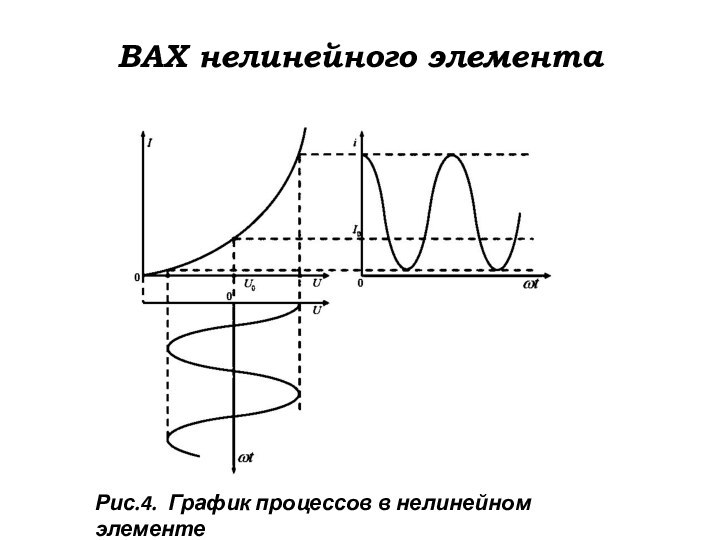
ВАХ нелинейного элемента
Рис.4. График процессов в нелинейном элементе
Слайд 24
Отклик нелинейной цепи
на входной гармонический сигнал
Вследствие нелинейности характеристики форма тока на выходе становится несинусоидальной.
Причину этого искажения гармони-ческого колебания можно пояснить следующим образом.
Поскольку функция тока обладает периодичностью, то её можно представить тригонометрическим рядом Фурье:
................. (6)
Слайд 25
Пусть суммарное напряжение источников смещения и
входного гармонического сигнала
................ (7)
приложено к нелинейному элементу, ВАХ
которого в окрестности рабочей точки аппроксимирована полиномом Тейлора вида:
....... (8)
Подставив формулу (7) в выражение (8), получим:
.....
Слайд 26
Используя известные формулы разложения степеней косинусов,
получим:
Выполнив подстановки и упростив выражения, запишем общее
выражение для тока нелинейной цепи в компактной форме:
..... (9)
Слайд 27
Здесь постоянная составляющая и амплитуды гармоник
тока:
.....
......... (10)
Слайд 28
Спектр тока в цепи с НЭ при кусочно-линейной
аппроксимации его характеристики
Пусть суммарное гармоническое и
постоянное напряжение вида (7) подаётся на вход электрической цепи с НЭ, характеристика которого аппроксимирована кусочно-линейной линией и описывается формулой (5). В этом случае временнáя диаграмма тока, протекающего через нелинейные цепи, имеет форму косинусоидальных импульсов с отсечкой их нижней части (рис.5).
Слайд 29
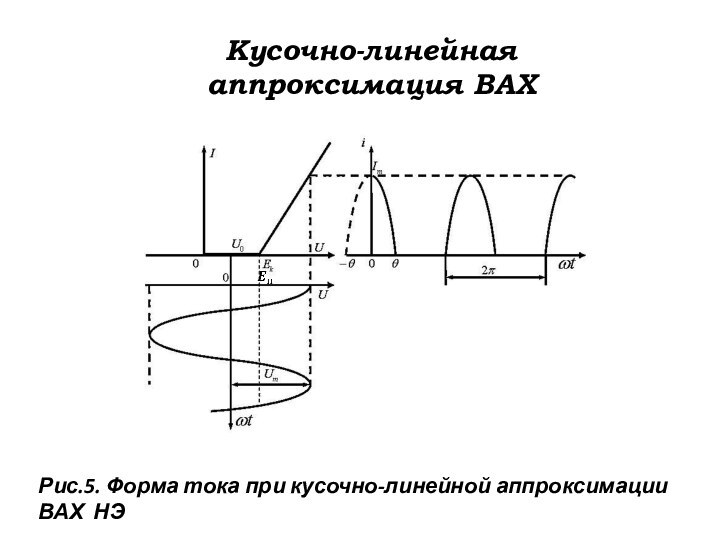
Кусочно-линейная
аппроксимация ВАХ
Рис.5. Форма тока при кусочно-линейной аппроксимации
ВАХ НЭ
Слайд 30
Кусочно-линейная
аппроксимация ВАХ
(Другое определение этого параметра: угол, соответствующий
половине той части периода, в течение которой в выходной
цепи нелинейного элемента протекает ток, называется углом отсечки и обозначается буквой ).
.......... (11)
Слайд 31
Кусочно-линейная аппроксимация ВАХ
...... (12)
Слайд 32
Кусочно-линейная аппроксимация ВАХ
В этих импульсах тока
постоянная составляющая запишется следующим образом:
..... (13)
Амплитуда первой гармоники:
.... (14)
...........
(15)
Слайд 33
Функции (коэффициенты) Берга
В радиотехнике полученные результаты
записываются в специальной форме:
...........
....... (16)
Слайд 34
Функции (коэффициенты) Берга
............ (17)
Коэффициенты гармоник
очень часто используются в инженер-ных расчётах, например, при проектировании
схем нелинейных уси-лителей мощности, умножителей частоты и автогенераторов. Поэтому они приводятся в специальной литературе.
Слайд 36
Нелинейный резонансный усилитель мощности
В радиопередающих
устройствах широкое применение находят резонансные усилители мощности и умножители
частоты.
Слайд 37
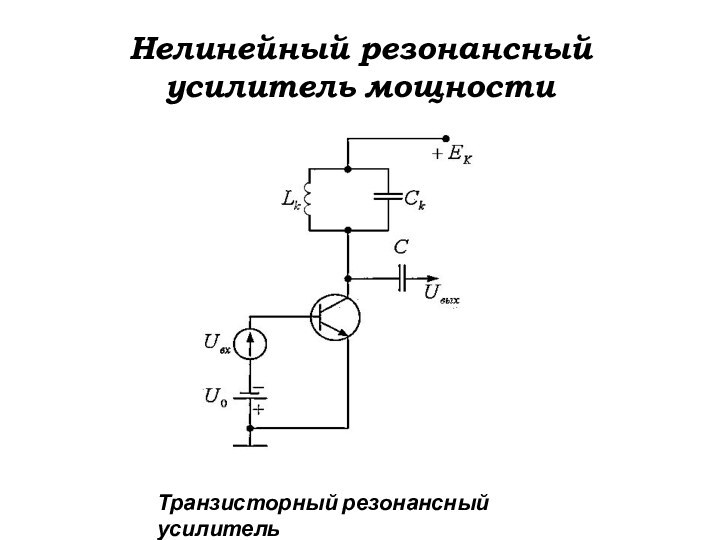
Нелинейный резонансный усилитель мощности
Транзисторный резонансный усилитель
Слайд 38
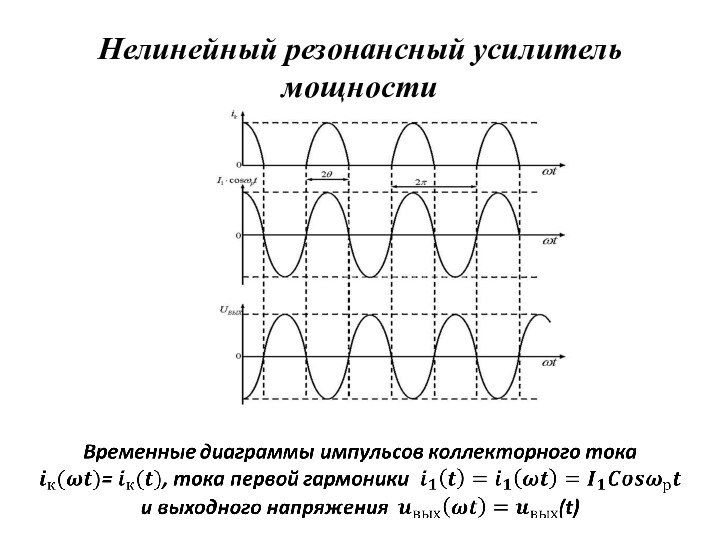
Нелинейный резонансный усилитель мощности
Слайд 39
Нелинейный резонансный усилитель мощности
Слайд 40
Нелинейный резонансный усилитель мощности
Используя формулу (16)
для коэффициентов Берга, запишем выра-жение для амплитуды выходного напряжения
................... (18)
Слайд 41
Умножитель частоты
Необходимость в умножителях частоты
возникает при разра-ботке высокостабильных источников гармонических колебаний повышенной частоты,
когда непосредственное генерирование сиг-налов такого диапазона затруднительно.
Наличие в спектре коллекторного тока гармонических составля-ющих с частотами, кратными входной частоте, позволяют использовать нелинейный резонансный усилитель в качестве умножителя частоты.