Слайд 2
Рекомендуемая литература
В.И. Нефёдов «Основы радиоэлектроники и связи», 2009
г
С.И. Баскаков «Радиотехнические цепи и сигналы», 2003 г.
С.И. Баскаков
«Радиотехнические цепи и сигналы.
Руководство к решению задач», 2002 г.
4. М.Т. Иванов, А.Б. Сергиенко, В.Н. Ушаков,
«Теоретические основы радиотехники», 2002 г.
5. М.П. Медиченко, В.П. Литвинов «Радиотехнические цепи и
сигналы, т.1; 2», 2011 г.
Слайд 3
Спектральная плотность мощности шума
……… (1)
Слайд 4
Отношение сигнал/шум
При обнаружении сигнала в
шумах наиболее эффективен критерий максимума отношения сигнал/шум по мощности
на выходе фильтра. Линейный фильтр, для которого это отно-шение максимально, называют
оптимальным (наилучшим, или согласованным) фильтром, а также коррелятором.
Слайд 5
Отношение сигнал/шум
……… (2)
……… (3)
где:
Слайд 7
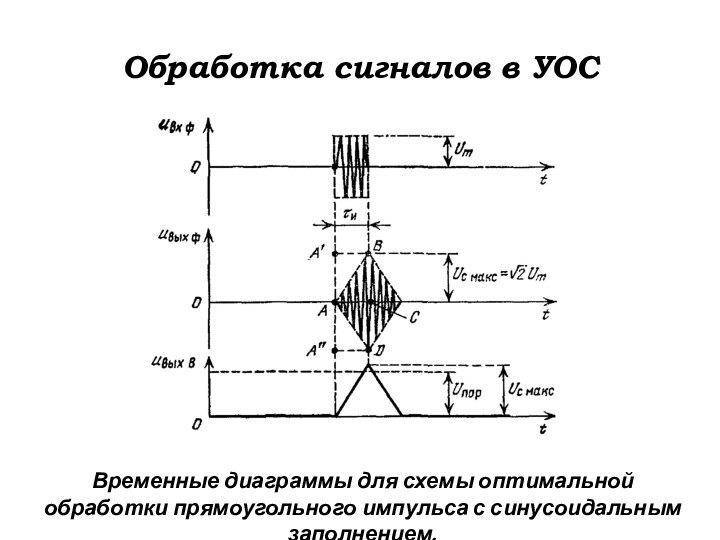
Обработка сигналов в УОС
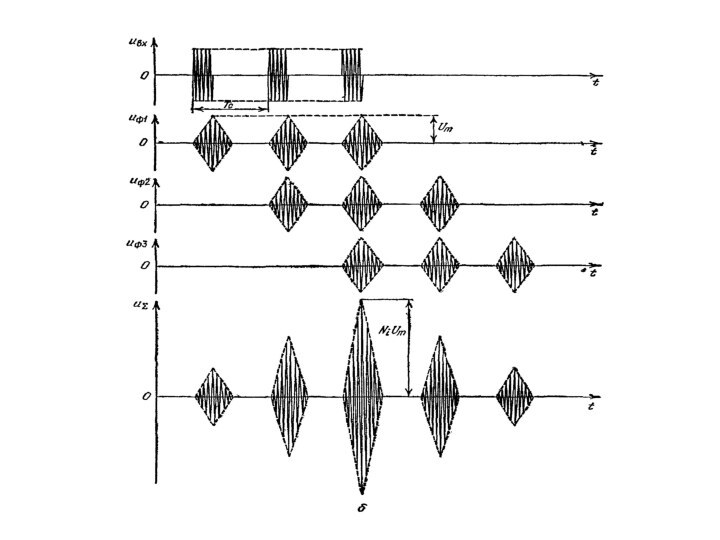
Временные диаграммы для схемы оптимальной
обработки прямоугольного импульса с синусоидальным заполнением.
Слайд 8
Обработка сигналов в УОС
……… (4)
Отсюда
энергия каждого импульса
……… (5)
Слайд 9
Обработка сигналов в УОС
……… (6)
Слайд 10
Обработка сигналов в УОС
Приравнивая правые
части формул (5) и (6), находим
……… (7)
……… (8)
Слайд 11
Обработка сигналов в УОС
……… (9)
……… (10)
а отношение сигнал/шум
по напряжению
……… (11)
Слайд 13
Оптимальная фильтрация одиночного сигнала
Если АЧХ
оптимального фильтра будет совпадать по форме
с амплитудно-частотным спектром
сигнала, то выходное напряжение сигнала будет пропорционально квадрату входного напряжения, а выходное напряжение шума будет пропорцио-нально первой степени входного напряжения сигнала. Тем самым улучшается соотношение сигнал/шум, так как фильтр совсем не пропускает шумы на частотах, где нет составляющих спектра сигнала, остальные же составляющие этого спектра воспроизводятся с тем бóльшим коэффициентом передачи, чем больше их интенсивность по сравнению с шумами.
Слайд 14
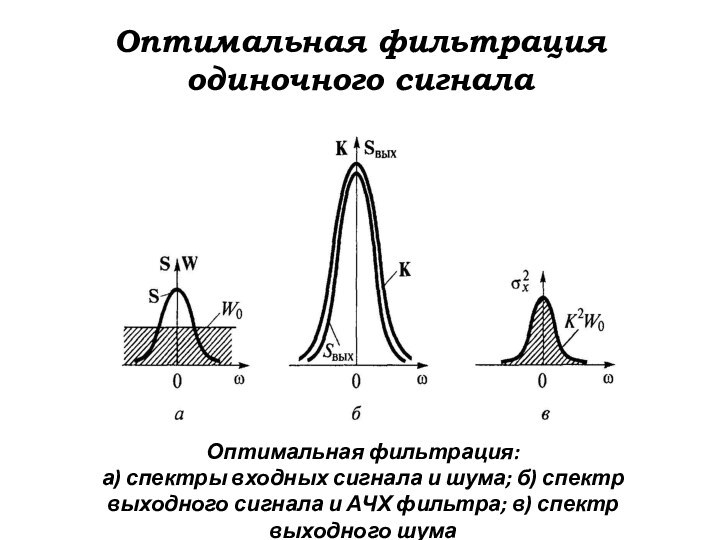
Оптимальная фильтрация одиночного сигнала
Оптимальная фильтрация:
а) спектры входных сигнала
и шума; б) спектр выходного сигнала и АЧХ фильтра;
в) спектр выходного шума
Слайд 15
Оптимальная фильтрация одиночного сигнала
Сущность метода
обработки принимаемого сигнала оптимальным фильтром.
Результаты математического
анализа показывают, что коэффициент передачи оптимального фильтра (АЧХ фильтра), максимизирующего отношение сигнал/шум, имеет вид:
……… (12)
……… (13)
ФЧХ фильтра
Слайд 16
Оптимальная фильтрация одиночного сигнала
Слайд 17
Оптимальная фильтрация одиночного сигнала
Из множества
же спектральных компонентов входного белого шума, располагающихся в бесконечной
полосе частот, на выход фильтра проходят и не ослабляются только те, которые находятся под кривой его АЧХ, т. е. в ограниченной полосе частот. Это приводит к ослаблению средней мощно-сти шума на выходе фильтра по сравнению со спектральной плотностью мощности белого шума на входе.
В результате такого действия отношение сигнал/шум
на выходе оптимального фильтра увеличивается.
Слайд 18
Оптимальная фильтрация одиночного сигнала
Слайд 19
Оптимальная фильтрация одиночного сигнала
Слайд 20
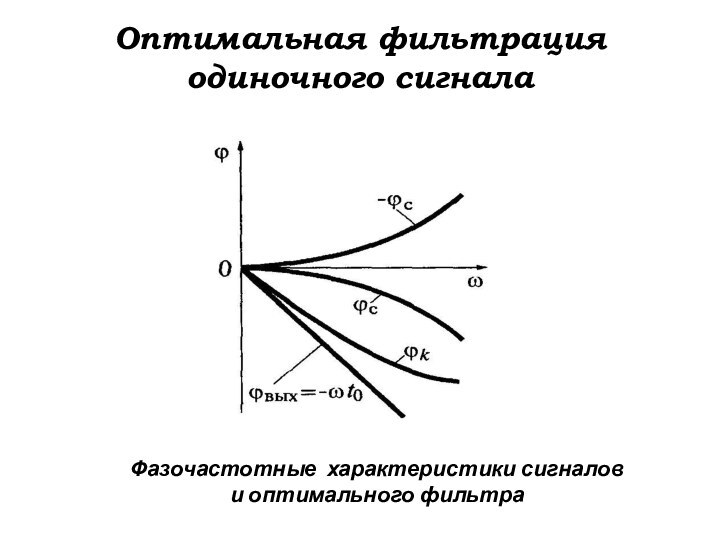
Оптимальная фильтрация одиночного сигнала
Фазочастотные характеристики сигналов
и оптимального
фильтра
Слайд 21
Оптимальная фильтрация одиночного сигнала
Фазовая характеристика
выходного сигнала, определяемая формулой
……… (14)
показана прямой линией.
Слайд 22
Оптимальная фильтрация одиночного сигнала
Таким образом, коэффициент передачи фильтра,
описываемый известным уже соотношением
……… (15)
согласован с амплитудным и
фазовым (или фазовой характери-стикой) спектрами входного сигнала. Поэтому рассмотренный оптимальный линейный фильтр часто называют согласованным.
Слайд 23
Оптимальная фильтрация одиночного сигнала
Из сказанного следуют два важных
вывода:
Слайд 24
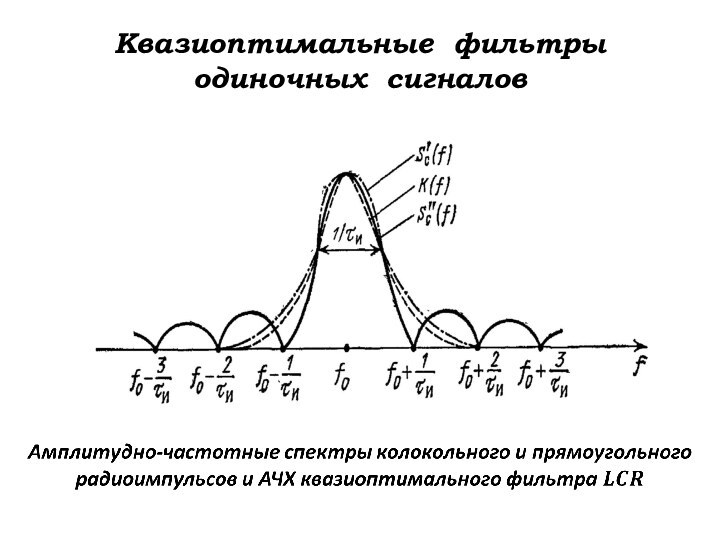
Квазиоптимальные фильтры
одиночных сигналов
Слайд 25
Квазиоптимальные фильтры
одиночных сигналов
Слайд 26
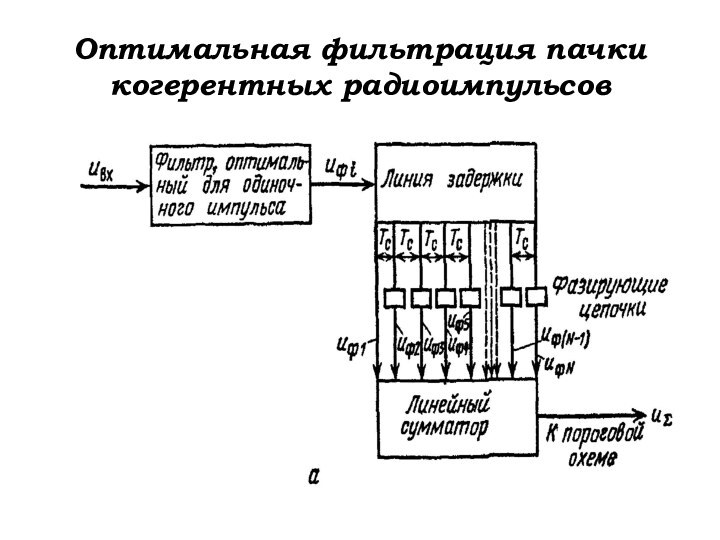
Оптимальная фильтрация пачки когерентных радиоимпульсов
Когерентность
– это согласованное протекание во времени нескольких колебательных или
волновых процессов.
Если разность фаз двух колебаний остаётся постоянной во времени или меняется по строго определённому закону, то колебания называются когерентными. Колебания,
у которых разность фаз изменяется беспорядочно и быстро по сравнению с их периодом, называются некогерентными.
Излучение считается когерентным, если начальные фазы всех импульсов в пачке одинаковые или закономерно изменяются от импульса к импульсу. Если это условие не соблюдается, то излучение некогерентное.
Слайд 27
Оптимальная фильтрация пачки когерентных радиоимпульсов
Слайд 28
Оптимальная фильтрация пачки когерентных радиоимпульсов
Слайд 30
Оптимальная фильтрация пачки когерентных радиоимпульсов
Слайд 31
Оптимальная фильтрация пачки когерентных радиоимпульсов
…… (16)
Слайд 32
Гребенчатый фильтр
и общей полосой пропускания
Слайд 33
Гребенчатый фильтр
В этих выражениях:
Слайд 34
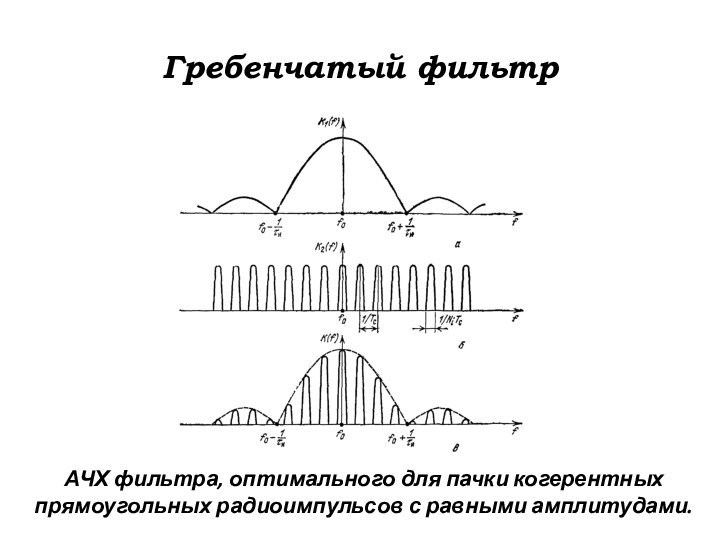
Гребенчатый фильтр
АЧХ фильтра, оптимального для пачки когерентных прямоугольных
радиоимпульсов с равными амплитудами.
Слайд 35
Гребенчатый фильтр
Расчёты и практика показывают,
что реализовать гребен-чатый фильтр достаточно трудно – для этого
требуется множество элементарных фильтров с весьма узкой полосой прозрачности каждого.
Общая полоса прозрачности гребенчатого фильтра
Слайд 36
Обработка сигнала
при оптимальном приёме
Дальнейшая
обработка сигнала при оптимальном приёме происходит в видеодетекторе. Если
производится обработка пачки некогерентных сигналов, то используется обычный детектор огибающей
(амплитудный детектор).
Если же производится обработка пачки когерентных импульсов, то в качестве детектора используется
синхронный фазовый детектор,
называемый также
когерентным детектором.
Слайд 37
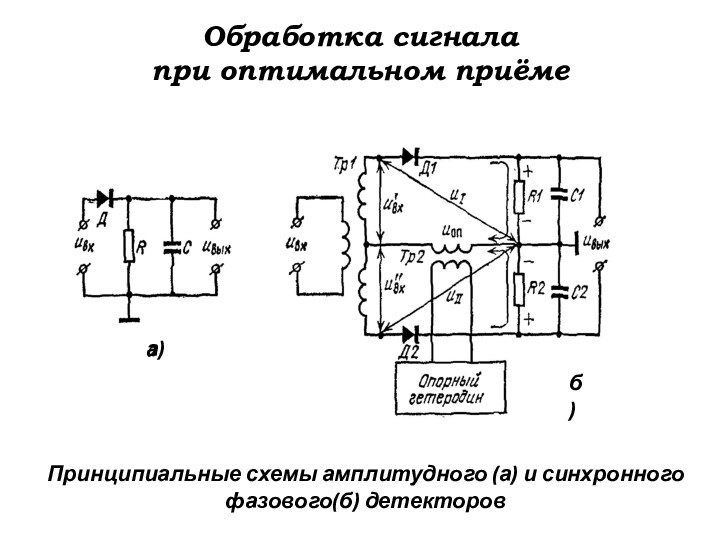
Обработка сигнала
при оптимальном приёме
Принципиальные схемы амплитудного (а)
и синхронного фазового(б) детекторов
а)
б)
Слайд 38
Оптимальная фильтрация некогерентных импульсов
Строго закономерная
связь между фазами сигналов, необхо-димая для когерентного приёма, достигается,
как правило, применением сложных устройств. Поэтому более широко используется менее эффективный, но легче осуществляемый некогерентный приём.
Слайд 39
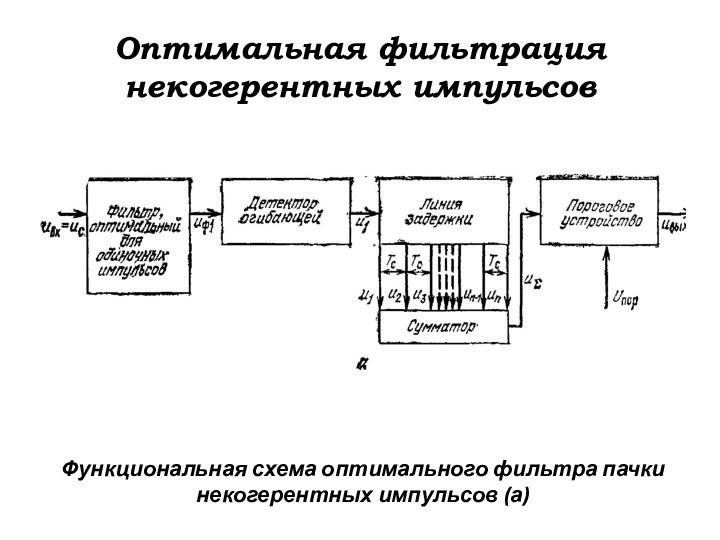
Оптимальная фильтрация некогерентных импульсов
Функциональная схема оптимального фильтра пачки
некогерентных импульсов (а)
Слайд 40
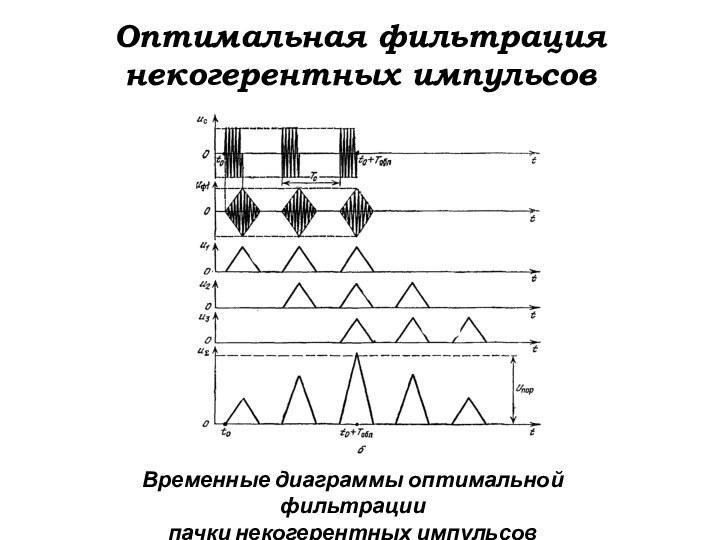
Оптимальная фильтрация некогерентных импульсов
Временные диаграммы оптимальной фильтрации
пачки
некогерентных импульсов
Слайд 41
Оптимальная фильтрация некогерентных импульсов
Такая последовательность
обработки объясняется тем, что отсутствие закономерной связи между начальными
фазами сигналов исключает возможность додетекторного интегрирования и применения синхронного фазового детектора.
Слайд 42
Оптимальная фильтрация некогерентных импульсов
Слайд 43
Оптимальная фильтрация некогерентных импульсов
Эффективность оптимальной
обработки некогерентных сигналов снижается за счёт потерь при детектировании
и интегрировании. Потери детектирования могут оказаться значительными вследствие того, что оптимальной фильтрации одиночного импульса (а не всей пачки) может быть недостаточно для получения сильного сигнала на входе детектора.
Слайд 44
Оптимальная фильтрация некогерентных импульсов
Слайд 45
Корреляционная обработка сигналов
…… (17)
…… (18)
Слайд 46
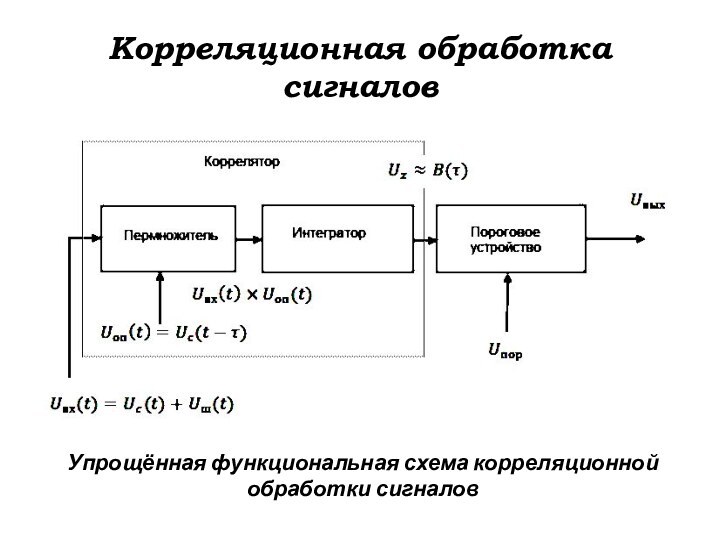
Корреляционная обработка сигналов
Упрощённая функциональная схема корреляционной
обработки сигналов
Слайд 47
Корреляционная обработка сигналов
Слайд 48
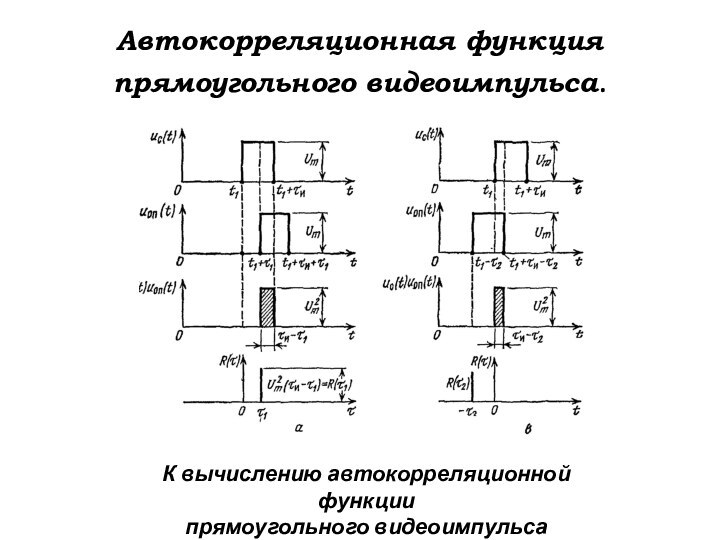
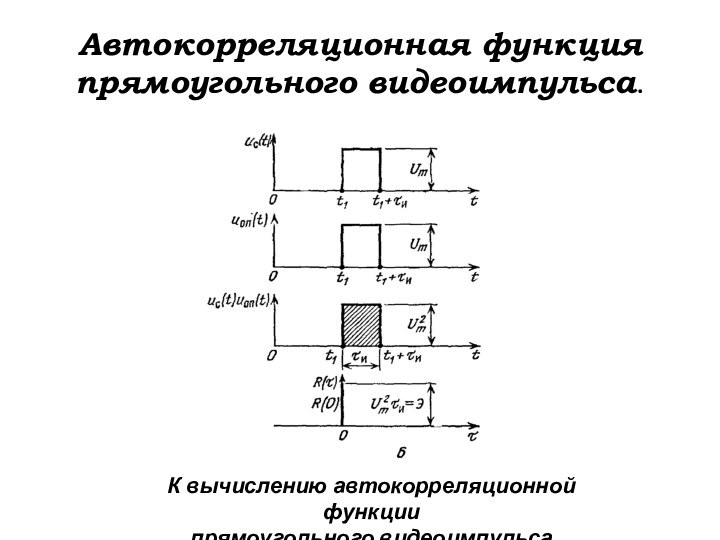
Автокорреляционная функция
прямоугольного видеоимпульса.
К вычислению автокорреляционной функции
прямоугольного видеоимпульса
Слайд 49
Автокорреляционная функция
прямоугольного видеоимпульса.
К вычислению автокорреляционной функции
прямоугольного видеоимпульса
Слайд 50
Автокорреляционная функция
прямоугольного видеоимпульса.
Слайд 51
Автокорреляционная функция
прямоугольного видеоимпульса.
Слайд 52
Автокорреляционная функция
прямоугольного видеоимпульса.
Слайд 53
Автокорреляционная функция
прямоугольного видеоимпульса.
Автокорреляционная функция прямоугольного
видеоимпульса
Слайд 54
Автокорреляционная функция
прямоугольного видеоимпульса.
Слайд 55
Автокорреляционная функция
прямоугольного видеоимпульса.
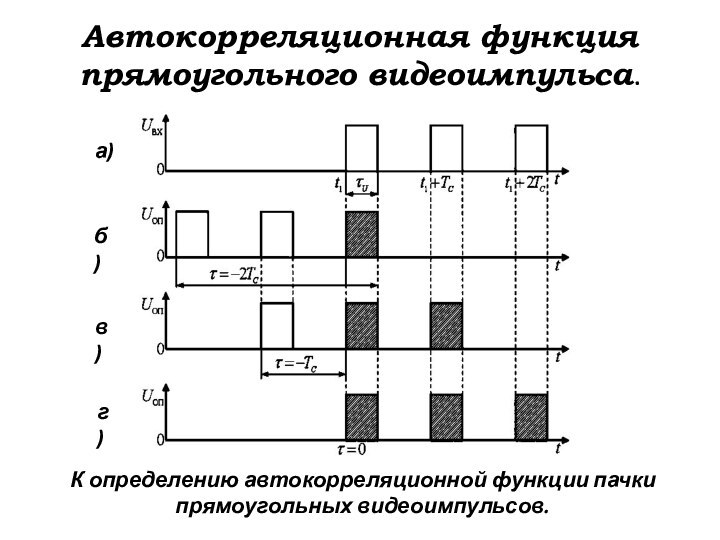
К определению автокорреляционной функции пачки
прямоугольных видеоимпульсов.
а)
б)
в)
г)
Слайд 56
Автокорреляционная функция
прямоугольного видеоимпульса.
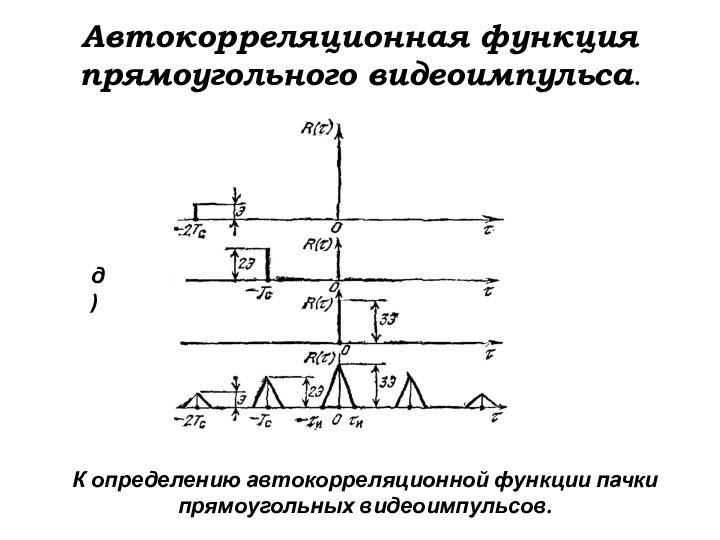
К определению автокорреляционной функции пачки
прямоугольных видеоимпульсов.
д)
Слайд 57
Автокорреляционная функция
прямоугольного видеоимпульса.
Слайд 58
Автокорреляционная функция
прямоугольного видеоимпульса.
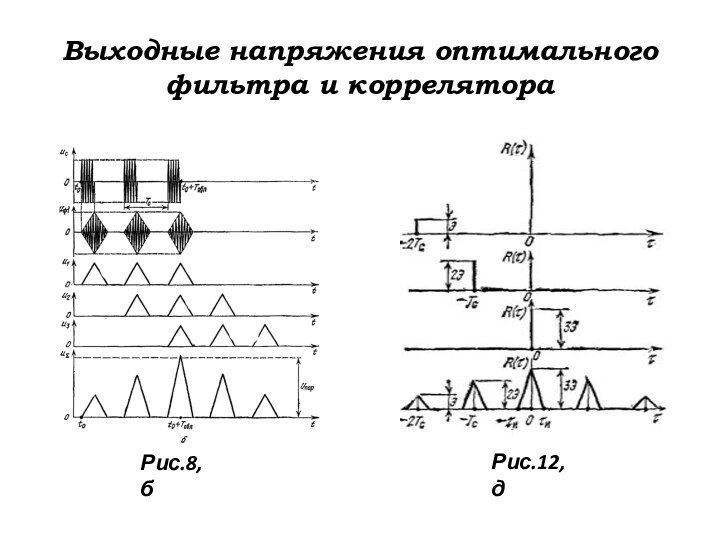
Сопоставляя рис.12, д
и рис.8, б, убеждаемся в полном совпадении выходных напряжений
оптимального фильтра
и коррелятора. Это не случайно: оптимальная фильтрация
и корреляционная обработка сводятся по существу
к внутрипериодному интегрированию одиночного импульса
и, кроме того, к межпериодному интегрированию в случае пачки импульсов.
Слайд 59
Выходные напряжения оптимального фильтра и коррелятора
Рис.8, б
Рис.12, д
Слайд 60
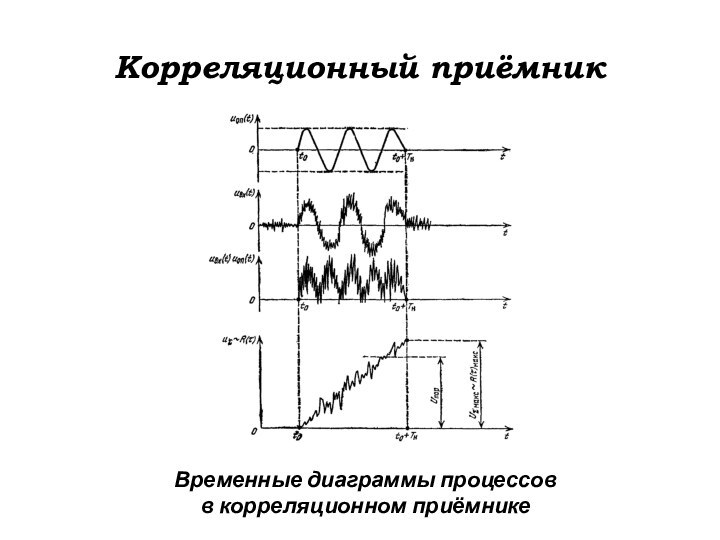
Корреляционный приёмник
Временные диаграммы процессов
в корреляционном приёмнике
Слайд 61
Корреляционный приёмник
которое равно нулю, когда нет опорного напряжения,
а следовательно, и сигнала.
Слайд 62
Корреляционный приёмник
….. (18)
Слайд 64
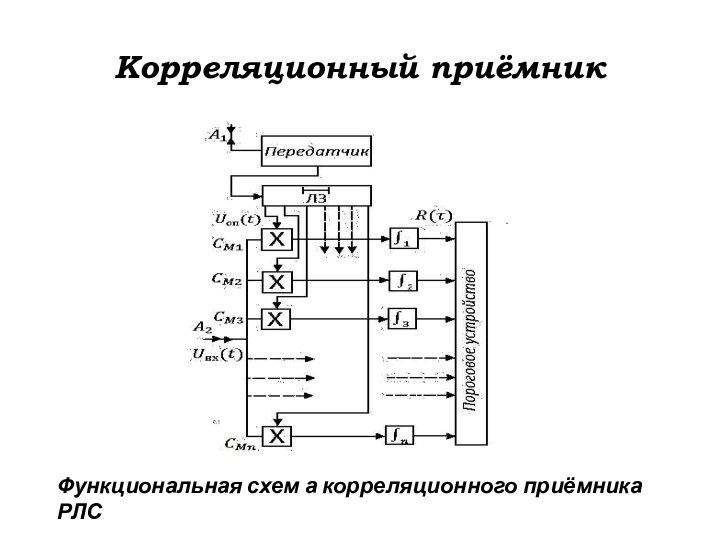
Корреляционный приёмник
Функциональная схем а корреляционного приёмника РЛС
Слайд 65
Корреляционный приёмник
Опорное напряжение для коррелятора
получают ответв-лением незначительной части излучения передатчик в линию задержки.
Значение задержки должно быть равно времени запаздывания отражённого сигнала (эхо-сигнала). Если это равенство не соблюдается, то опорный и отражённый сиг-налы не совпадают во времени, они не коррелируются и напряжение на выходе фильтра (интегратора) не достигает порогового. В связи с этим коррелятор должен быть многоканальным.
Слайд 66
Корреляционный приёмник
Так как через пороговую
схему проходят сигналы из тех каналов, где запаздывание эхо
- сигнала совпадает с задержкой опорного напряжения, то имеется возможность использовать это устройство и как многоканальный измеритель дальности.
Слайд 67
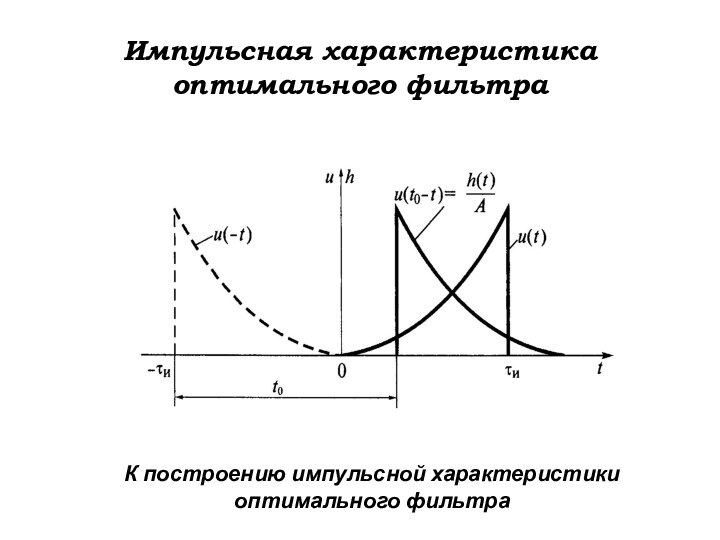
Импульсная характеристика оптимального фильтра
Чтобы определить
импульсную характеристику оптимального фильтра, вычислим обратное преобразование Фурье от
частотного коэффициента передачи.
Используя уже применяемую ранее формулу для определения импульсной характеристики через коэффициент передачи
получим
……(19)
Слайд 68
Импульсная характеристика оптимального фильтра
……(20)
Слайд 69
Импульсная характеристика оптимального фильтра
……(21)
Слайд 70
Импульсная характеристика оптимального фильтра
Слайд 71
Импульсная характеристика оптимального фильтра
К построению импульсной характеристики
оптимального
фильтра
Слайд 72
Построение импульсной характеристики оптимального фильтра
Слайд 73
Свойства оптимального фильтра
Фундаментальной особенностью оптимального
фильтра является то, что обнаружение с его помощью сигнала
в шумах зависит не от формы, а от его энергии.
В частности, за счёт увеличения длительности входного импульса можно надёжно обнаруживать сигналы небольшой амплитуды в шумах. Однако при этом приходится проигрывать в скоростях обработки информации.