- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Векторы
Содержание
- 2. Понятие вектораМногие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами
- 3. Понятие вектораОтрезок, для которого указано, какая его
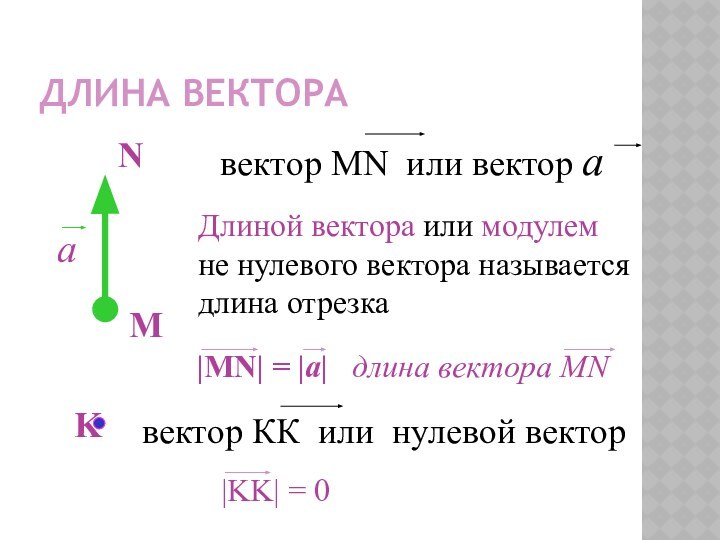
- 4. Длина вектораДлиной вектора или модулем не нулевого вектора называется длина отрезка
- 5. Нулевой вектор считается коллинеарным любому векторуКоллинеарные вектораНенулевые
- 6. Сонаправленные вектораКоллинеарные вектора имеющие одинаковое направление, называются сонаправленными векторами
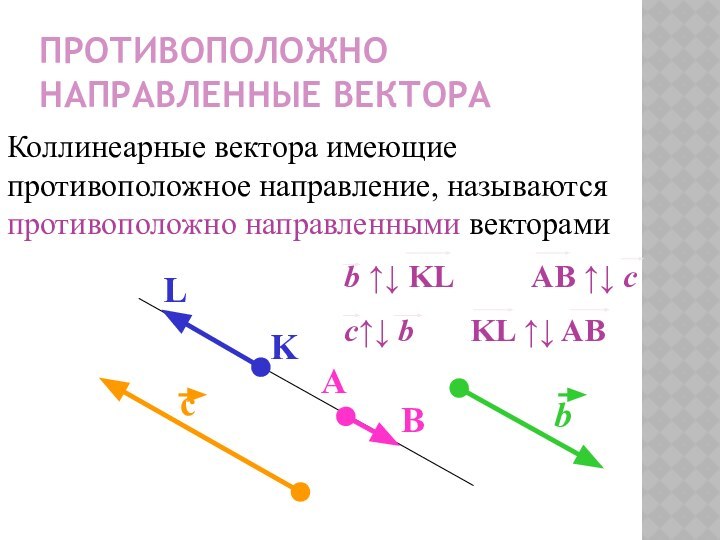
- 7. Противоположно направленные вектораКоллинеарные вектора имеющие противоположное направление, называются противоположно направленными векторами
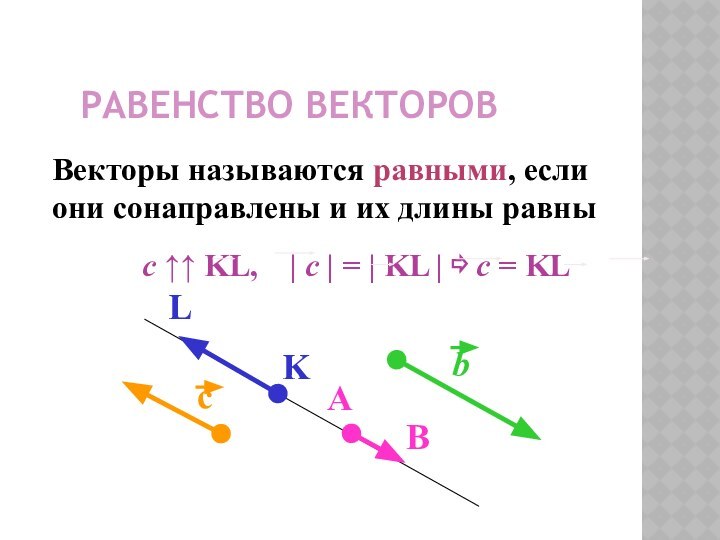
- 8. Равенство векторовВекторы называются равными, если они сонаправлены и их длины равны
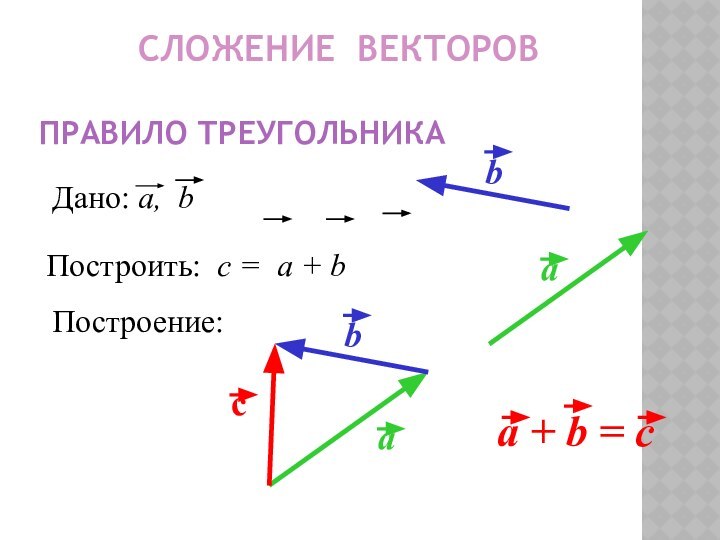
- 9. Сложение векторов Правило треугольникаПостроение:
- 10. Сложение векторов Правило параллелограммаПостроение:
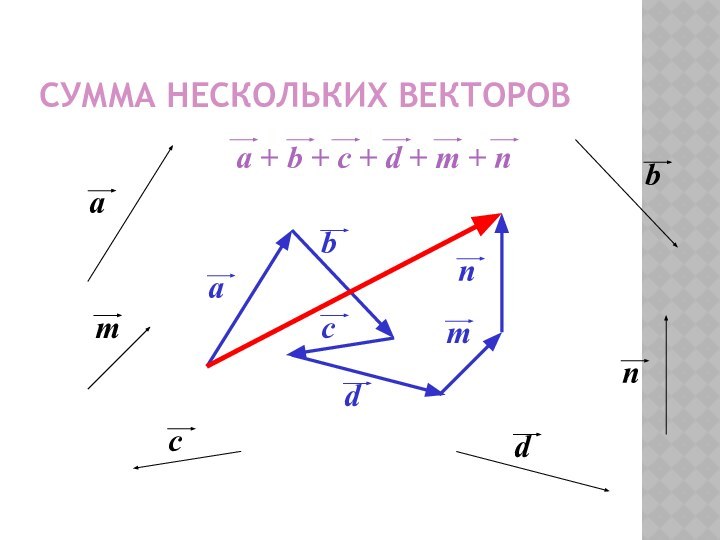
- 11. Сумма нескольких векторов
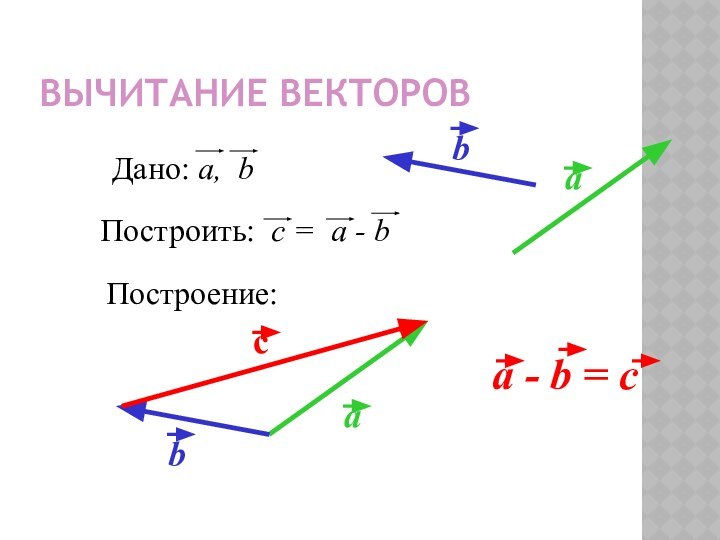
- 12. Вычитание векторовПостроение:
- 13. Умножение вектора a на число kk·a =
- 14. векторное пространство Множество векторов с действительными компонентами,
- 15. Свойства:х+у=у+х – коммутативное (переместительное) свойство сложения.(х+у)+z=x+(y+z) –
- 16. Линейное пространствоОтметим, что под х, у, z
- 17. Скалярным произведением двух векторов
- 18. Приложения скалярного произведения:Угол меду векторами:Условие перпендикулярности ненулевых векторов:
- 19. Приложения скалярного произведения:Работа постоянной силы: Пусть материальная
- 20. Евклидово пространствоСкалярное произведение имеет свойства:1°. ху=ух –
- 21. Линейное (векторное) пространство, в котором задано скалярное
- 22. Векторное произведение1.2.
- 23. Скачать презентацию
- 24. Похожие презентации
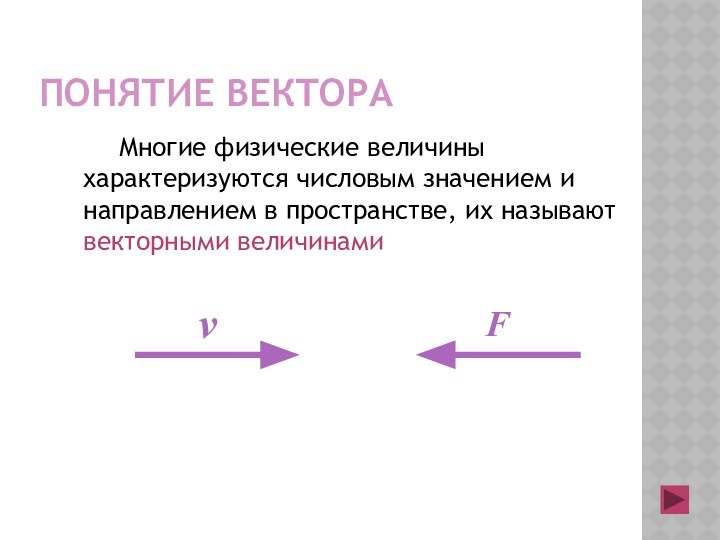
Понятие вектораМногие физические величины характеризуются числовым значением и направлением в пространстве, их называют векторными величинами












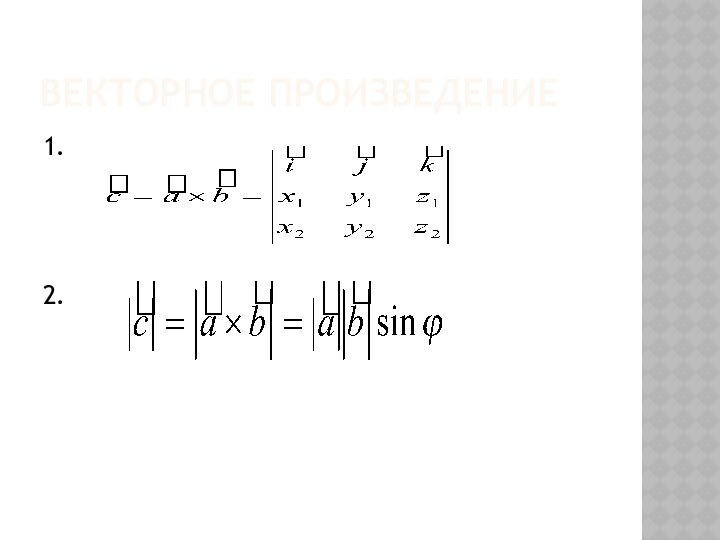

Слайд 2
Понятие вектора
Многие физические величины характеризуются числовым значением и
направлением в пространстве, их называют векторными величинами
Слайд 3
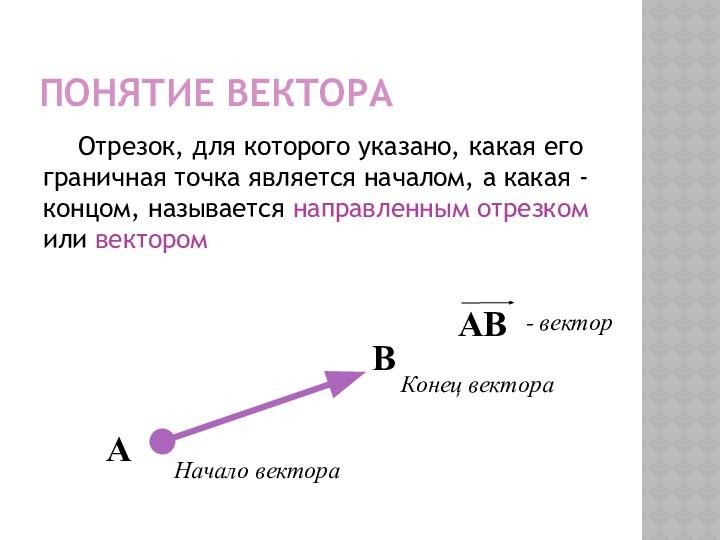
Понятие вектора
Отрезок, для которого указано, какая его граничная
точка является началом, а какая - концом, называется направленным
отрезком или векторомКонец вектора
Начало вектора
- вектор
Слайд 5
Нулевой вектор считается коллинеарным любому вектору
Коллинеарные вектора
Ненулевые вектора
называются коллинеарными, если они лежат на одной прямой или
на параллельных прямых
Слайд 6
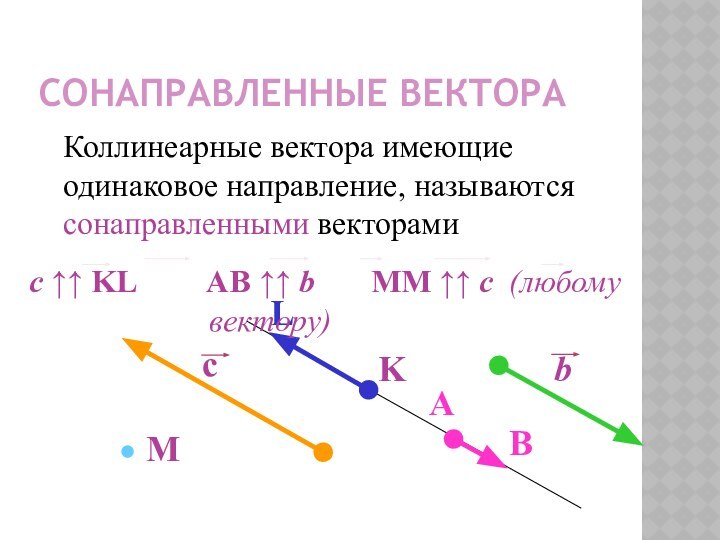
Сонаправленные вектора
Коллинеарные вектора имеющие одинаковое направление, называются сонаправленными
векторами
Слайд 7
Противоположно направленные вектора
Коллинеарные вектора имеющие противоположное направление, называются
противоположно направленными векторами
Слайд 13
Умножение вектора a на число k
k·a = b,
|a|
≠ 0, k – произвольное число
|b| = |k|·|a|,
если
k>0, то a ↑↑ bесли k<0, то a ↑↓ b
Слайд 14
векторное пространство
Множество векторов с действительными компонентами, в
котором определены операции сложения векторов и умножения вектора на
число, удовлетворяющее приведенным ниже восьми свойствам (рассматриваемым как аксиомы)
Слайд 15
Свойства:
х+у=у+х – коммутативное (переместительное) свойство сложения.
(х+у)+z=x+(y+z) – ассоциативное
(сочетательное) свойство сложения.
α(βх)=(αβ)х – ассоциативное свойство относительно числового множителя.
α(х+у)=αх+αу
– дистрибутивное (распределительное) свойство относительно суммы векторов.(α+β)х=αх+βх – дистрибутивное свойство относительно суммы числовых множителей.
Существует нулевой вектор 0=(0;0;…0) такой, что х+0=х для любого вектора х.
Для любого вектора х существует противоположный вектор (-х) такой, что х+(-х)=0.
1*х=х для любого вектора х.
Слайд 16
Линейное пространство
Отметим, что под х, у, z можно
рассматривать не только векторы, но и элементы (объекты) любой
природы. В этом случае множество элементов называется линейным пространством.
Слайд 18
Приложения скалярного произведения:
Угол меду векторами:
Условие перпендикулярности ненулевых векторов:
Слайд 19
Приложения скалярного произведения:
Работа постоянной силы:
Пусть материальная точка
перемещается прямолинейно из положения в положение под действием постоянной
силы , образующей угол с перемещением:
Слайд 20
Евклидово пространство
Скалярное произведение имеет свойства:
1°. ху=ух – коммутативное
свойство
2°. х(у+z)=xy+xz – дистрибутивное свойство
3°. (αх)у=α(ху) – для любого
действительного числа α4°. хх>0, если х – ненулевой вектор, хх=0, если х – нулевой вектор.





























