- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Расстояния в пространстве
Содержание
- 2. Цель занятия: научиться находить расстояния:-между
- 3. Для успешного решения задач
- 4. Простейшие задачи
- 5. Задача №1Ребро куба ABCDA1B1C1D1 равно 2. Найти
- 6. Решение:1) Соединим точки В1 и М и
- 7. Задача №2 Ребро куба
- 8. Решение:1)Проведем диагонали куба и обозначим точку их
- 9. Задача №3Ребро куба ABCDA1B1C1D1 равно 2. Найти
- 10. Решение:1)AC перпендикулярна плоскости BDD1В1 2)В плоскости
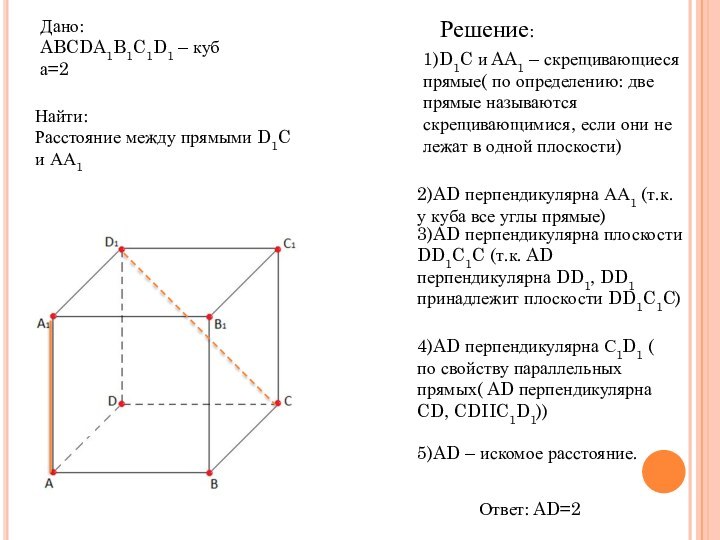
- 11. Задача №4 Ребро куба ABCDA1B1C1D1 равно 2. Найти расстояние между прямыми D1C и AA1
- 12. Решение:1)D1C и AA1 – скрещивающиеся прямые( по
- 13. Типичные задачи из части С2 ЕГЭ
- 14. Задача №1 В кубе ABCDA1B1C1D1
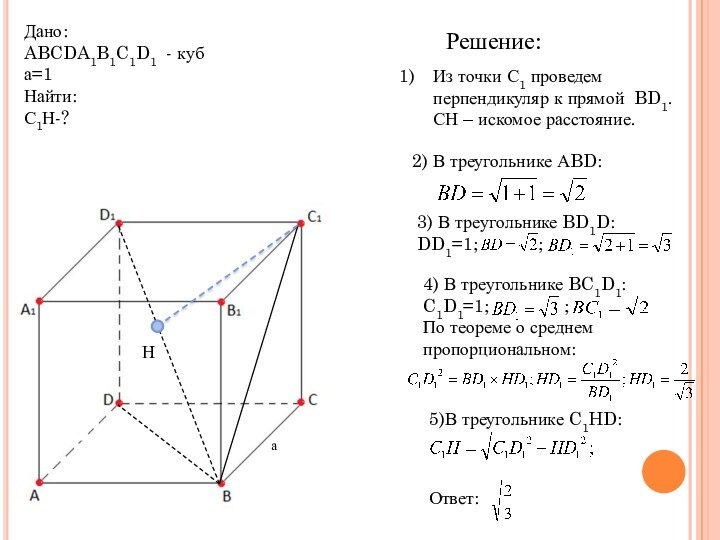
- 15. Решение:Из точки С1 проведем перпендикуляр к прямой BD1. СН – искомое расстояние.
- 16. Задача №2 В кубе ABCDA1B1C1D1 все ребра
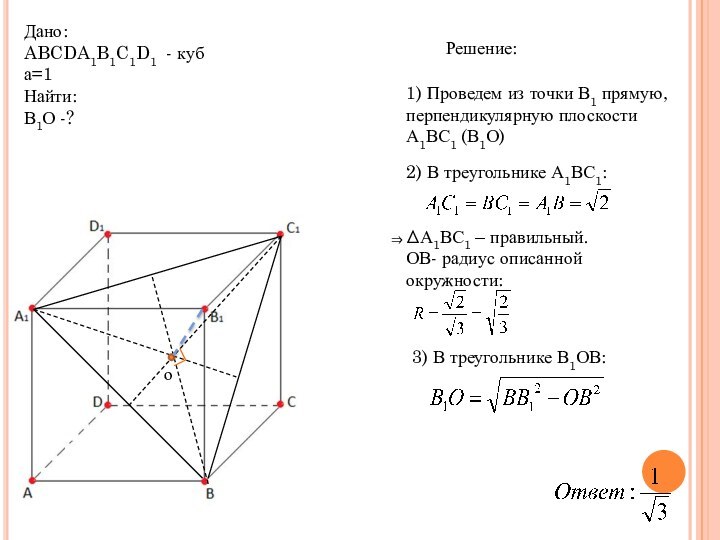
- 17. Решение:1) Проведем из точки В1 прямую, перпендикулярную плоскости А1ВС1 (В1О)
- 18. Задачи для самостоятельной работы
- 19. 1)В кубе ABCDA1B1C1D1 ребро равно 1. О1-точка
- 20. Скачать презентацию
- 21. Похожие презентации
Цель занятия: научиться находить расстояния:-между точками;-от точки до прямой;-от точки до плоскости;-между скрещивающимися прямыми.














Слайд 3 Для успешного решения задач повторите
определения указанных расстояний и следующие теоремы:
- о перпендикулярности прямой
и плоскости,- о перпендикулярности плоскостей,
- о трех перпендикулярах,
- о перпендикулярности двух параллельных прямых плоскости,
о параллельности двух прямых, перпендикулярных одной плоскости,
о параллельности прямой и плоскости,
о параллельности плоскостей.
Повторить определения и теоремы можно по любому учебнику геометрии (стереометрия) для 10-11 классов.
Слайд 5
Задача №1
Ребро куба ABCDA1B1C1D1 равно 2. Найти расстояние
между точками В1 и М, где М – середина
ребра АD.
Слайд 6
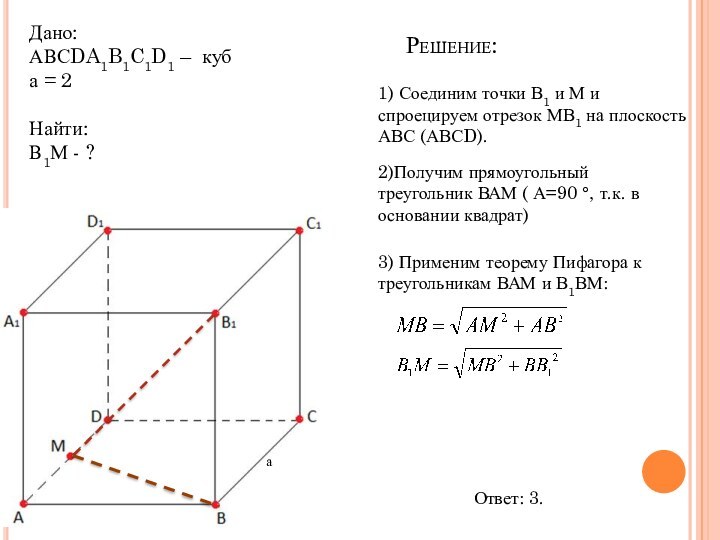
Решение:
1) Соединим точки В1 и М и спроецируем
отрезок МВ1 на плоскость АВС (АВСD).
2)Получим прямоугольный треугольник ВАМ
( А=90 °, т.к. в основании квадрат)3) Применим теорему Пифагора к треугольникам ВАМ и В1ВМ:
Ответ: 3.
Слайд 8
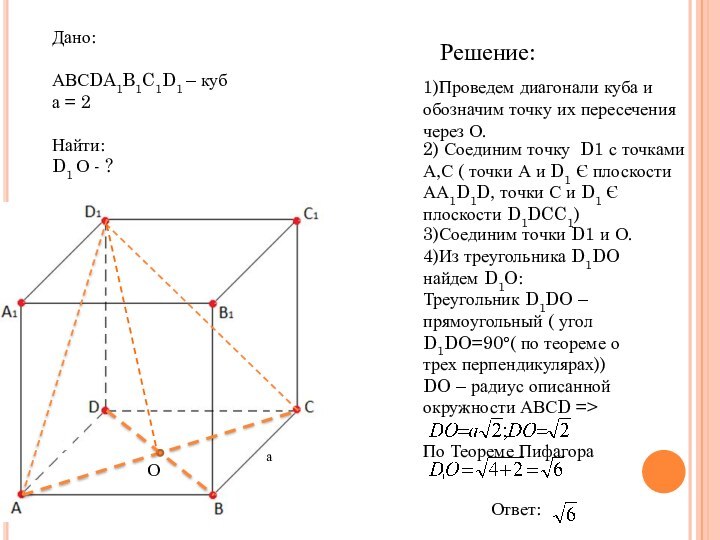
Решение:
1)Проведем диагонали куба и обозначим точку их пересечения
через О.
2) Соединим точку D1 с точками А,С (
точки А и D1 Є плоскости АА1D1D, точки С и D1 Є плоскости D1DCC1)3)Соединим точки D1 и О.
Слайд 9
Задача №3
Ребро куба ABCDA1B1C1D1 равно 2. Найти расстояние
от точки М, середины ребра СC1, - до плоскости
DBB1.
Слайд 10
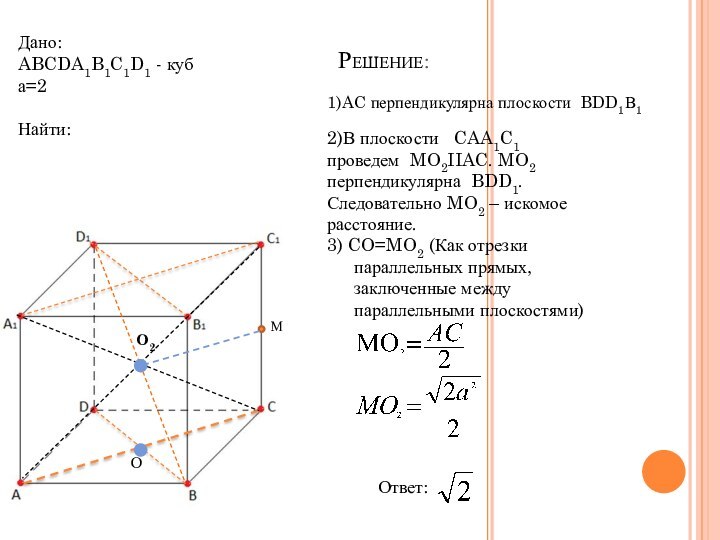
Решение:
1)AC перпендикулярна плоскости BDD1В1
2)В плоскости CAA1C1
проведем MO2IIAC. MO2 перпендикулярна BDD1. Следовательно MO2 – искомое
расстояние.
Слайд 12
Решение:
1)D1C и AA1 – скрещивающиеся прямые( по определению:
две прямые называются скрещивающимися, если они не лежат в
одной плоскости)2)AD перпендикулярна АА1 (т.к. у куба все углы прямые)
3)AD перпендикулярна плоскости DD1C1C (т.к. AD перпендикулярна DD1, DD1 принадлежит плоскости DD1C1C)
4)AD перпендикулярна С1D1 ( по свойству параллельных прямых( AD перпендикулярна CD, CDIIC1D1))
5)AD – искомое расстояние.
Ответ: AD=2
Слайд 16
Задача №2
В кубе ABCDA1B1C1D1 все ребра равны
1. Найдите расстояние от точки В1 до плоскости А1ВС1.
Слайд 19 1)В кубе ABCDA1B1C1D1 ребро равно 1. О1-точка пересечения
диагоналей верхней грани. Найти расстояние от О1 до прямой
ВС.2) В кубе ABCDA1B1C1D1 ребро равно 1. Найти расстояние от точки М – середины ребра ВВ1 – до плоскости АСС1.