Презентация на тему Решение транспортных задач линейного программирования.

Проектирование маршрутов городского транспорта.
Задача 1.



 Выбор трассы

новой автобусной линии в городе. Построен за городом новый жилой микрорайон, который нужно связать с центром города. Имеем исходную стратегическую игру(Ω ,A,L). Статистик пришел к выводу, что линию можно провести до пункта А1, или А2, или А3.Решение А = {а1, а2, а3}, где a1, означает проведение трассы до А1, а2 - до А2, а3 - до А3, причем А1 иА3 находятся в разных концах города. Множеством состояний природы Ω являются Θ1, Θ2, Θ3 - состояния, когда большинство жителей микрорайона работает соответственно в окрестности пунктаА1, пункта А2 и пункта А3, находящегося в самом центре города. Если принятое решение провести трассу не будет удовлетворять нужды жителей микрорайона, то транспортное предприятие понесет потери. Потери будут максимальными при ошибочном решении проложить трассу к пункту А3 вместо А1 или на­оборот. Решение. Функция L(Θ, а) потерь характеризуется матри­цей (табл.1).

(Ω, A, L) в статистическую (Ω, D, R) при учете информации о действительном

состоянии природы. Для этого проводится выборочный опрос жителей микрорайона. Результаты этого опроса образуют вектор

опрошенных (не менее 50 %), которые предлагают строительство трассы

до пунктов А1, А2, A3 соответственно; x4 — любое из трех направлений не получило решающего количества голосов. Действительные данные результата опроса показали следующие вероятности рекомендаций жителей (табл. 2) в зависимости от состояний природы Θ.

вероятности P(x1|Θ1) = P(x2|Θ2) = P(x3|Θ3) = 0,7. Пусть d(x) = а - нерандомизированная функция решения, преобразующая

множество Х результатов эксперимента в множество решений. Множество D  нерандомизированных решений при наличии четырех результатов эксперимента и трех возможных решений будет иметь 34 = 81 различную функцию решений статистика в статистической игре с природой (Ω, D, R}. Из них мы ограничимся шестью допустимыми функциями: d1, d2, ... , d6 (табл. 3).

функции решения — это все функции dϵD, которые не ставят в

соответствие хотя бы одному из результатов x1, x2, x3 решение а1, а2, a3 потому, что для этих функции значение риска R(Θ, d) будет всюду большим по сравнению с другими функциями решений. Результат х4 при этом во внимание не принимается, поскольку он не отражает конструктивного предложения.

Таблица 3.

потерь, вычислим математические ожидания функций потерь, т. е. получим

функции риска для допустимых функций решений:

х2 х3, х4 решение d4 будет соответствовать решению а1, d5→a2, d6→a3. Объединим все полученные решения в

табл. 4 и выпишем минимальные значения функции риска по строке и максимальные значения - по столбцу.


Таблица 4.

функций решений нет минимаксной функции: v1=0

надо искать во множестве D* рандомизированных функций δ. В данной статистической игре (Ω, D, R) в качестве оптимальной нужно принять минимаксную функцию решения. Для того чтобы найти рандомизированную минимаксную функцию решения δ0, следует обратиться к линейному программированию . Пусть δ - распределение вероятностей на множестве нерандомизированных функций решения d. Обозначим это распределение η1 = P(d1), η2 = P(d2), ... ,η6 = P(d6). Теперь обозначим через υ цену расширенной статистической игры (Ω, D*, R) при рандомизации функций решений и запишем в терминах линейного программирования задачу статистика, который решает ее в интересах транспортного предприятия. Для этого воспользуемся данными табл. 4:

введем дополнительные переменные q7, q8, q9. В результате перейдем от неравенств

к равенствам:

при qj > 0, j =  . Решим эту задачу линейного программирования симплексным методом (техника решения известна и здесь не излагается) и получим базисное оптимальное решение: q1 = q3 = 2/7; q2 = q4 = q5 = qб = 0. Значит, Zmax = q1 + q3 = 2/7 +2/7 = 4/7. Отсюда υ = l/Zmax = 2/7 = 1,75.

ηi - вероятности, с которыми следует сочетать соответствующие нерандомизированные функции решения di (i = 

). После перемножения получим рандомизированные функции δ: Итак, получена минимаксная рандомизированная функция решения δ0 с распределением вероятностей: P(d1) = 1/2; P(d3) = 1/2. Как ее охарактеризовать? Это смешанная стратегия δ0 с одинаковыми вероятностями чистых функций решения d1 и d3. Они различаются только результатом статистического эксперимента.

маршрута новой автобусной линии получена оптимальная минимаксная функция решения: •

если по эксперименту с анкетами получен результат х1, или x2, или x3, то следует принять решение а1 или а2, или a3 соответственно; • если получен результат х4, то нужно использовать механизм случайного выбора между решениями а1 (трассу вести до А1) и a3 (трассу вести до А3) с одинаковыми вероятностями, равными 0,5. Следует сделать одно важное замечание: в данном случае мы из расчетов получили одинаковые вероятности. (Это решение не имеет ничего общего с принципом равновероятности, который иногда необоснованно применяется при отсутствии информации о возможных вероятностях событии.)

сосредоточены запасы какого-либо однородного товара в определенных количествах, несколько

пунктов назначения, которые хотят получить этот товар в определенных количествах. Известно, что сумма заявок на получение груза из всех пунктов назначения равна сумме запасов товара, находящегося во всех пунктах отправления. Известна стоимость перевозки единицы товара от каждого пункта отправления до каждого пункта назначения. Требуется составить такой план перевозок, чтобы:
Все грузы из всех пунктов отправления были вывезены;
Заявки всех пунктов назначения были бы удовлетворены;
Суммарные затраты на перевозку были бы минимальны.
Рассмотрим конкретный пример.
Пусть имеется:
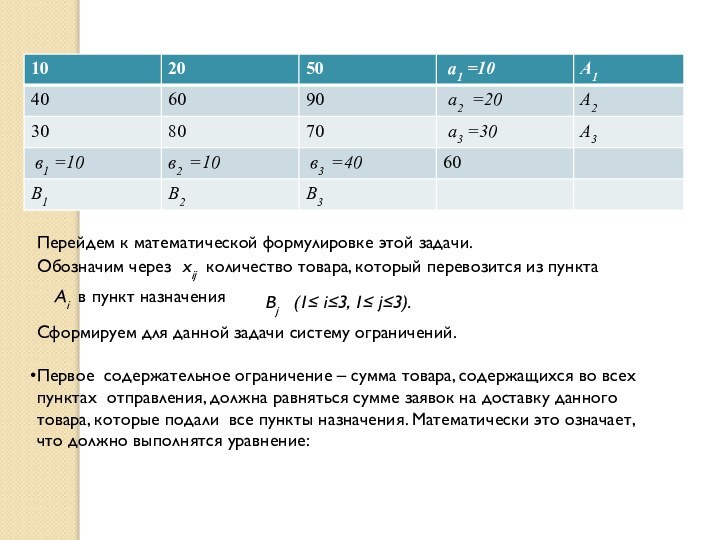
Три пункта отправления: города под названием  А1, А2,  А3, в которых сосредоточены запасы какого-либо товара (например машин) соответственно в количестве а1 =10, а2 =20, а3 =30;
три пункта назначения: города под названием В1, В2,  В3, в которых сосредоточены потребители товара, желающие получить его в количестве в1 =10, в2 =10, в3 =40;
установлено , что сумма заявок всех городов - потребителей товара равна суммарному количеству товара, т.е. :

= b1 + b2 + b3

=60

Известна стоимость перевозки одной единицы товара ( одной машины) из пункта отправления названием  Аi в пункт назначения Вi , т.е. задана матрица стоимостей перевозок:



С=



Требуется составить такой план перевозок, при котором весь имеющийся запас товара был бы из всех городов- поставщиков товара, являющихся пунктами отправления, вывезен, все заявки городов-потребителей удовлетворены, а стоимость перевозок всего товара , который перевозится от поставщиков к потребителям, была бы минимальна.

количество товара, который перевозится из пункта

 Аi в

пункт назначения

Bj (1≤ i≤3, 1≤ j≤3).

Сформируем для данной задачи систему ограничений.

Первое содержательное ограничение – сумма товара, содержащихся во всех пунктах отправления, должна равняться сумме заявок на доставку данного товара, которые подали все пункты назначения. Математически это означает, что должно выполнятся уравнение:

в данной задаче- все товары, содержащийся в каждом из

пунктов отправления, должны быть вывезены, возможно, различные пункты отправления. Математически это означает, что должны выполнятся следующие равенства:

в каждый пункт назначения изо всех пунктов отправления, должно

быть равно заявке, поданной данным пунктом. Математически это означает, что должны выполнятся следующие неравенства:

принимать отрицательное значение, т.е.


Цель задачи – в минимизации

перевозок. Математически это означает, что целевая функция


F=

F=

Таким образом, математическая задача состоит в нахождении такого плана перевозок X= ( ), который удовлетворял бы системе ограничений и составлял бы минимум целевой функции.
Отличительные особенности экономико-математической модели транспортной задачи:
Система ограничений представляет собой систему управлений;

два возможных значения: либо 0, либо 1;
Каждая переменная входит

в систему ограничений два раза.
Для математической формулировки транспортной задачи в общем виде введем следующие обозначения:
m- количество пунктов отправления, в которых сосредоточены товары;
аi - количество товара, сосредоточенного в пункте отправления Аi;
n- количество пунктов назначения, в которые должны быть перевезены товары;
bi – количество товара, которое заявлено пунктом Bj;
cij- стоимость перевозки единицы товара из пункта i в пункт j.
В этом случае система ограничений примет вид:

необходимо найти такой вектор X= (x 11, x12,…xmn), который

удовлетворял бы построенной системе ограничений и доставлял бы минимум целевой функции.
Важная особенность данной постановки задачи – соблюдение баланса между количеством товара, которые хотят приобрести по заявкам все пункты назначения, и количеством груза, имеющегося во всех пунктах отправления.
Такие транспортные задачи называются закрытыми. При несоблюдении этого условия транспортные задачи называются открытыми.

решена симплекс- методом. Однако в силу отмеченных выше особенностей

для нахождения ее оптимального решения могут быть применены и специальные методы решения ( например метод потенциалов).