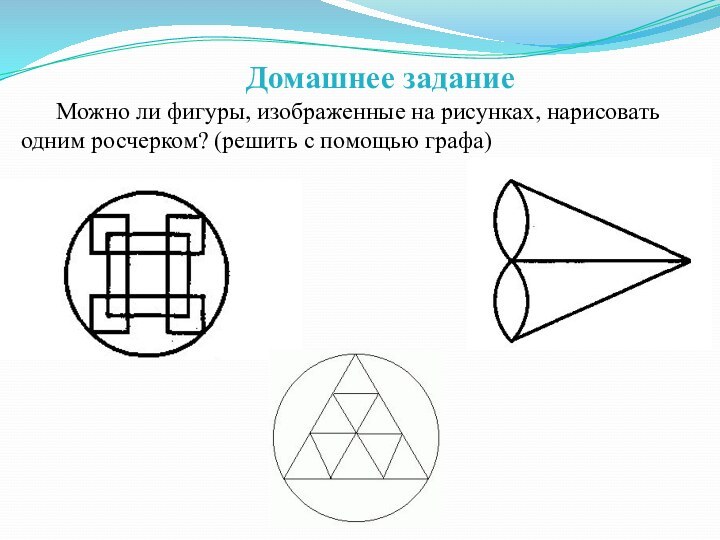
Презентация на тему Решение задач на Эйлеровы графы

математику Л.Эйлеру, появилась в 1736г. Вначале теория графов казалась

довольно незначительным разделом математики, так как она имела дело в основном с математическими развлечениями и головоломками. Однако дальнейшее развитие математики и особенно её приложений дало сильный толчок развитию теории графов. Уже в XIX столетии графы использовались при построении схем.

все ребра графа.
Эйлеровым циклом или эйлеровой цепью называется цикл,

содержащий все ребра графа и притом по одному разу. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Замкнутую линию, если ее можно начертить, не отрывая карандаша от бумаги, проходя при этом каждый участок в точности один раз, принято называть уникурсальной. Рисунок графа, обладающего эйлеровым путем или циклом, является уникурсальной линией.
Теорема 1. Если граф G(V,E) обладает эйлеровым циклом, то он связный и все его вершины четные.
Теорема 2. Если граф G(V,E) связный и все его вершины четные, то он обладает эйлеровым циклом.

мосты, проходя только один раз через каждый из этих

мостов?

тогда обход, о котором идет речь, возможен, и начать

этот обход можно с любого участка. Если же из этих вершин две нечетные, то и тогда можно совершить переход, как это предписано, но только начало обхода непременно должно быть взято в одной из этих двух вершин, а конец обхода непременно должен быть во второй нечетной вершине. Если, наконец, больше двух нечетных вершин, то тогда такое движение вообще невозможно...".

Если граф имеет цикл, содержащий все ребра графа по одному разу, то такой граф называется эйлеровым графом

Другими словами, эйлеров граф – это граф,который можно нарисовать одним росчерком

острова и берега, а ребра – мосты.
2. Определить

степень каждой вершины и подписать возле нее.
3. Посчитать количество нечетных вершин.
4. Обход возможен:
a. ЕСЛИ все вершины – четные, и его можно начать с любого участка.
b. ЕСЛИ 2 вершины – нечетные, но его нужно начать с одной из нечетных местностей.
5. Обход невозможен, если нечетных вершин больше 2.
6. Сделать ВЫВОД.
7. Указать Начало и Конец пути.

G. Если существует, найдите его.
Проверь себя!
  Решение:
    А) Так

как каждая вершина имеет чётную степень, то по критерию в этом графе существует эйлеров цикл: 1,4,6,9,10,8,5,3,2,4,7,10,11,8,6,5,2,1
    Б) В этом графе также каждая вершина имеет чётную степень, значит, существует и эйлеров цикл:  1,2,3,4,5,3,1,4,5,2,1
    В) Здесь каждая вершина имеет степень 5, то есть нечётную, следовательно, в этом графе (по критерию) нет эйлерова цикла.

и выход, чтобы можно было провести экскурсию по всем

залам, побывав в каждом из них в точности один раз?

Решение:
В этом графе вершины А и В имеют степень 3, то есть нечётную, следовательно, в нём существует эйлеров путь с началом в одной из этих вершин и концом в другой. Значит, вход и выход следует установить в вершинах А и В.

Проверь себя!

имеют эйлеров цикл.

вершина имеет чётную степень, то по критерию эйлерова графа,

данный граф имеет эйлеров цикл:
     a b e j i f c b d h j g f a c d e h g i a
б)  Этот граф связный, но т.к. все его вершины имеют  нечётную степень, то он не имеет эйлерова цикла.
в)  Этот граф связный, но т.к. все его вершины имеют степень 3, то есть нечётную, то он не имеет эйлерова цикла.
г)  Данный граф связный,  степени вершин а и с имеют нечётную степень, значит, этот граф не имеет эйлерова цикла.

Проверь себя!