- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Ряды динамики
Содержание
- 2. Элементы и виды рядов динамики Рядом динамики,
- 3. Ряды динамики состоят из двух элементов:
- 4. Время ряда отвечает конкретным моментам или периодам, к которым относятся уровни.
- 5. По признакам времени ряды динамики могут быть двух видов: моментные интервальные.
- 6. Моментными называют такие ряды динамики, уровни которых
- 7. Численность постоянного населения г. Воронежа (на начало года)
- 8. Уровни моментного ряда суммированию не подлежат, так
- 9. В то же время определенный смысл имеет
- 10. Интервальным называют такой ряд, уровни которого характеризуют
- 12. Уровни интервальных рядов дают итоговые, результирующие показатели,
- 13. Приведение рядов динамики к сопоставимому видуОдной
- 14. Сопоставимость уровней ряда динамики достигается такими путями:а) одинаковый
- 15. б) обеспечением одинаковой полноты охвата разных частей
- 16. в) разным учетом границ территории; так, при
- 17. г) использование единой методологии расчета уровней динамического ряда;
- 18. д) обеспечение одинаковых единиц измерения уровней ряда;
- 19. ж) использованием специальных приемов сопоставимости
- 20. Специальные приемы сопоставимости рядов динамикисмыкание рядов динамики
- 22. С целью выявления тенденции изменения объема производства
- 24. 2) приведение рядов динамики к одному основанию,
- 25. Поэтому целесообразно сравнивать относительные показатели, выраженные в
- 26. ПРИМЕРИмеются данные о динамике выпуска продукции и
- 28. Необходимо выполнить сравнительный анализ приведенных трех рядов
- 30. Анализ данных таблицы приводит к таким выводам:сравнение
- 31. анализ коэффициентов опережения (отношение темпов роста за
- 32. Следовательно, темпы роста факторов интенсивности производства (фондообеспеченость, электрообеспеченность) опережали темпы роста выхода валовой продукции;
- 33. 3. обеспечение одинаковости периодов интервального ряда, по
- 34. Например, необходимо построить ряд динамики реализации металлоконструкций
- 35. Показатели рядов динамикиДля оценки свойств динамики в
- 36. Расчет таких показателей базируется на сопоставлении уровней
- 37. Абсолютный прирост (или уменьшение) Δi соответствует скорости
- 38. Цепные и базисные абсолютные приросты связаны между собой зависимостью (сумма цепных приростов равняется конечному базисному):
- 39. Темп роста Ki. характеризует интенсивность изменений уровней
- 40. Произведение цепных темпов роста равняется конечному базисному:
- 41. Темп прироста Тi выражается в процентах и
- 42. Между темпом прироста и темпом роста существует такая связь:
- 43. Абсолютное значение одного процента прироста Аi характеризует
- 44. Расчет этого показателя имеет экономический смысл только
- 45. Абсолютное значение одного процента прироста Аi имеет
- 46. Необходимо отметить, что в динамических характеристиках (коэффициентах
- 47. В отличие от темпов прироста, которые нельзя
- 48. В состав аналитических показателей могут быть отнесены
- 49. При сопоставлении в динамике развития двух явлений
- 50. где и
- 51. С помощью этих коэффициентов могут сопоставляться ряды
- 52. Средние показатели рядов динамикиДля нахождения обобщающих характеристик
- 53. Методы вычисления средних уровней динамических рядов зависят от статистической структуры показателей.
- 54. В интервальном ряду с равными интервалами времени
- 55. В моментных динамических рядах с равными промежутками
- 56. Если отрезки времени между датами для моментных
- 57. Если для моментного ряда динамики есть данные
- 58. К средним из аналитических показателей относятся: средний абсолютный прирост; средний темп роста; средний темп прироста.
- 59. Средний абсолютный прирост характеризует среднюю скорость роста
- 60. Средний темп роста показывает, во сколько раз
- 61. Эту формулу можно записать иначе, если учесть,
- 62. На основе среднего темпа роста определяет средний
- 63. ВЫВОДДля всесторонней характеристики изменения социально-экономических явлений во
- 64. Методы обработки динамических рядов При анализе рядов
- 65. Часто уровни ряда со временем изменяются (колеблются),
- 66. Изучая ряды динамики, исследователи пытаются выявить главным
- 67. К способам и методам выравнивания динамических рядов
- 68. Наиболее простым способом выравнивания динамических рядов является
- 69. Вновь образованный ряд будет содержать увеличенные уровни,
- 70. ПримерДаны сведения об объеме реализации продукции помесячноЯнварь
- 71. Разные направления изменений по отдельным месяцам уровней
- 72. После увеличения интервалов основная тенденция роста продаж
- 73. Частным случаем рассмотренного способа является вычисление средних
- 74. Одним из распространенных методов выравнивания динамических рядов
- 75. Таким образом, каждый последующий интервал получается смещением
- 76. Получается новый ряд, составленный из скользящих средних.
- 77. Нахождение скользящей средней для четного количества уровней
- 78. В результате новый динамический ряд, построенный из
- 79. ПримерИспользование этого метода рассмотрим по данным о
- 81. Особенностью данных табл. является периодическое изменение квартальных
- 82. Для выявления тенденции развития методом скользящей средней
- 83. Поэтому при использовании метода скользящих средних их
- 86. Для четного числа уровней каждое значение скользящей
- 87. Для нахождения сглаженных уровней выполняется центрирование (графа
- 88. Полученные данные сглаженных уровней находятся в гр.
- 89. Недостатком выровненного ряда методом скользящей средней является
- 90. Использование в анализе рядов динамики способа увеличения
- 91. Сущность аналитического выравнивания динамического ряда заключается в
- 92. В основе метода лежит установление функциональной зависимости
- 93. При этом на практике чаще всего применяются
- 94. в) гиперболическая
- 95. На основе теоретического анализа выявляется характер развития
- 96. выравнивать динамические ряды по уравнению прямой линии
- 97. выравнивание динамических рядов по уравнению квадратичной параболы
- 98. выравнивание по степенной функции целесообразно использовать тогда,
- 99. В практической деятельности может возникнуть необходимость интерполяции
- 100. Интерполяция — это нахождение отсутствующих промежуточных уровней
- 101. Экстраполяция используется при прогнозировании общественных явлений в
- 102. На практике результат экстраполяции прогнозируемых уровней социально-экономических
- 103. где tg — коэффициент доверия t- распределения
- 104. Коэффициент доверия tg выбирается из статистических таблиц
- 105. Тогда окончательно с вероятностью P=1 — α
- 106. Измерение сезонных колебаний в рядах динамики
- 107. Скачать презентацию
- 108. Похожие презентации
Элементы и виды рядов динамики Рядом динамики, или динамическим рядом, называют ряд размещенных в хронологической последовательности численных данных (статистических показателей), которые характеризуют величину общественного явления на данный момент или за определенный период времени.



































































































Слайд 3
Ряды динамики состоят из двух элементов:
уровней ряда yi (i - 1...п)
времени
ti. Уровнями ряда называют численные данные того или другого показателя ряда динамики; они могут быть выражены в абсолютных, относительных и средних величинах и задаваться в табличной форме или графически.
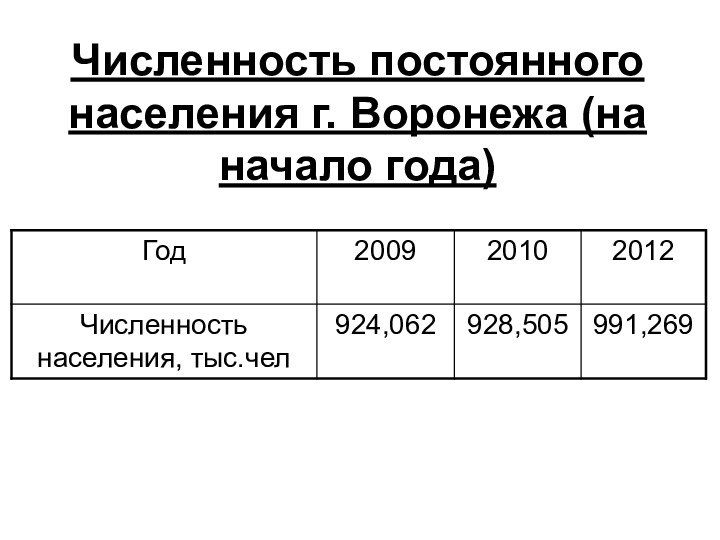
Слайд 6 Моментными называют такие ряды динамики, уровни которых фиксируют
состояние явления на данный момент времени (дату). Примером моментного
ряда динамики могут быть данные о численности населения г. Воронежа на начало года (тыс. чел.).
Слайд 8
Уровни моментного ряда суммированию не подлежат, так как
имеют элементы повторного счета (отдельные лица, которые учитывались в
2009 году, учитывались и в 2010 году).
Слайд 9
В то же время определенный смысл имеет расчет
разностей уровней моментного ряда, так как они характеризуют изменение
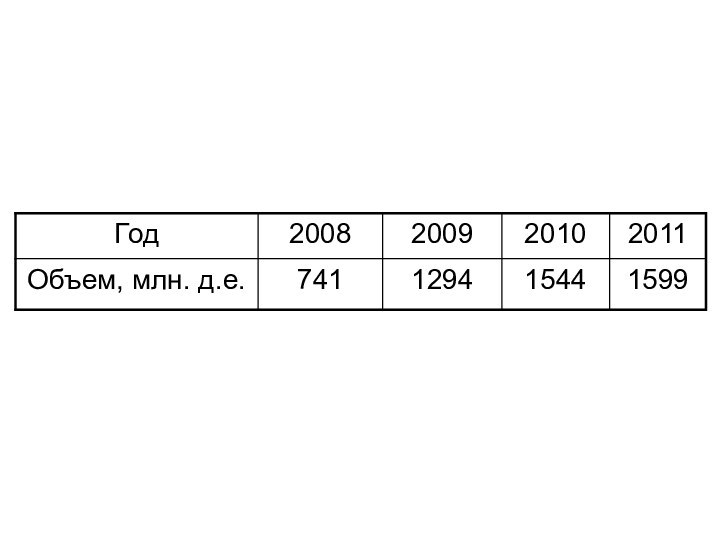
уровней за определенный промежуток времени: за период с 2009 по 2012 год численность населения увеличилась на 67,207 тыс. чел.Слайд 10 Интервальным называют такой ряд, уровни которого характеризуют явление
за определенный период времени. Примером интервального ряда динамики является
производство промышленной продукции региона за 2008-2011 гг.
Слайд 12
Уровни интервальных рядов дают итоговые, результирующие показатели, которые
отвечают интервалу времени, поэтому их можно складывать и делить.
При суммировании уровней ряда находят накопленные итоги.
Слайд 13
Приведение
рядов динамики к сопоставимому виду
Одной из самых
важных проблем построения рядов динамики является сопоставимость уровней этих
рядов, которая достигается либо в процессе сбора и обработки данных, либо путем их пересчета.
Слайд 14
Сопоставимость уровней ряда динамики достигается такими путями:
а) одинаковый подходом
к единицам совокупности на разных этапах формирования этой совокупности,
при котором учитывается сущность и цель явления, достигается однородность экономического содержания показателей ряда;Слайд 15 б) обеспечением одинаковой полноты охвата разных частей явления;
так, например, при характеристике динамики численности студентов высших учебных
заведений нельзя в одни годы учитывать только численность студентов дневной формы обучения, а в другие — численность студентов всех форм обучения;Слайд 16 в) разным учетом границ территории; так, при характеристике
экономического состояния страны необходимо использовать данные в изменяемых границах
территории, а при изучении темпов экономического развития — брать данные по территории в неизменных границах;Слайд 17 г) использование единой методологии расчета уровней динамического ряда; если
методология расчета уровней разная, то для сравнения уровней необходимо
пересчитать их по новой единой методологии;
Слайд 18
д) обеспечение одинаковых единиц измерения уровней ряда;
так,
количество продукции, произведенной в разные периоды, оценивают в ценах
одного периода, которые называют неизменными(фиксированными);
Слайд 20
Специальные приемы сопоставимости рядов динамики
смыкание рядов динамики с
целью получения единого ряда за весь период.
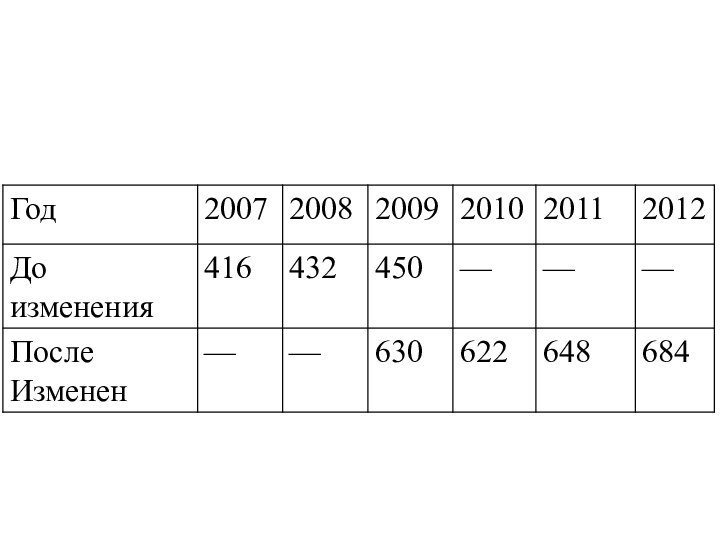
Например, имеются
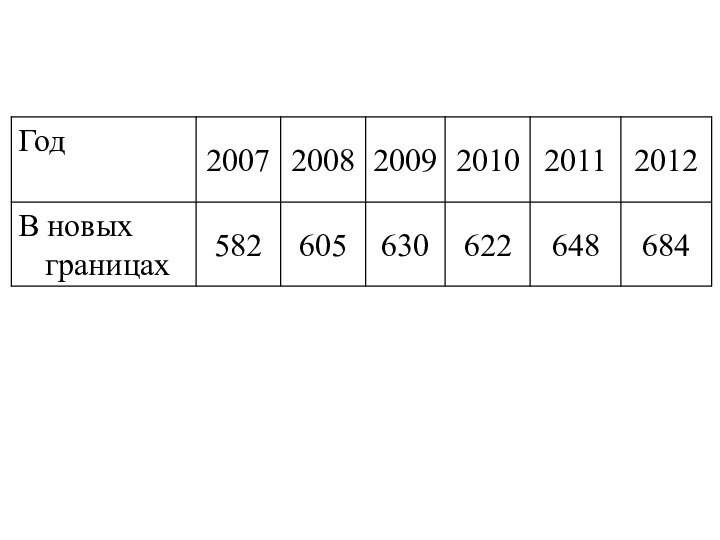
данные об объеме производства ОАО в составе которого произошли изменения в анализируемом периоде, то есть вошло новое предприятие в состав ОАО. Слайд 22 С целью выявления тенденции изменения объема производства и
приведения рядов динамики к сопоставимому виду необходимо осуществить их
смыкание. Для этого определяем в 2009 году коэффициент соотношения уровней двух рядов:Умножаем на этот коэффициент уровни первого ряда и достигаем его сопоставимости с уровнями второго ряда:
в 2007 г. — 416 • 1,4=582;
в 2008 г. — 432 • 1,4=605.
Слайд 24 2) приведение рядов динамики к одному основанию, то
есть к общей базе сравнения. При этом можно сравнивать
динамические ряды как одноименных, так и разноименных показателей применительно к разным территориям или составным частям целого. Абсолютные уровни таких рядов в силу разных причин могут быть несопоставимы.Слайд 25 Поэтому целесообразно сравнивать относительные показатели, выраженные в коэффициентах
или процентах, когда определяется одна общая база сравнения (единица
или 100%) и с ней сравнивают другие уровни ряда в относительном выражении.
Слайд 26
ПРИМЕР
Имеются данные о динамике выпуска продукции и основных
факторах интенсивности производства на предприятии за 2008-2012 гг. приведенные
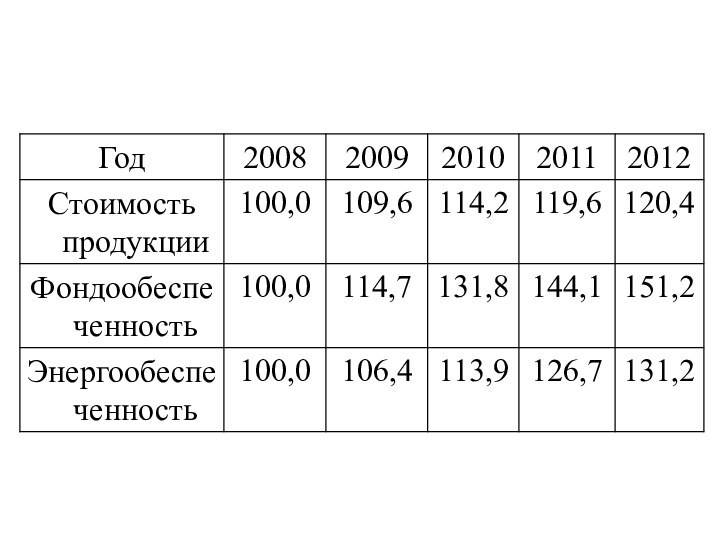
в таблицеСлайд 28 Необходимо выполнить сравнительный анализ приведенных трех рядов динамики,
используя их приведение к одной основе.
Сравнительный анализ разных рядов
динамики по абсолютным значениями их уровней невозможен в виду их различной природы и различных единиц измерения. Поэтому приведем сопоставимые ряды к одной основе, определив относительные уровни рядов: базисные темпы роста с постоянной базой сравнения — уровни за 2008 год. Полученные данные по базисным темпам роста в процентах приведены в таблице
Слайд 30
Анализ данных таблицы приводит к таким выводам:
сравнение темпов
роста выхода валовой продукции и факторов производства свидетельствуют об
опережающих темпах роста факторов интенсивности производства (в 1,3-1,5 раза) по сравнению с темпами роста выхода валовой продукции (в 1,2 раза). Это означает, что в хозяйстве выход валовой продукции в динамике на единицу факторов имел тенденцию к снижению;Слайд 31 анализ коэффициентов опережения (отношение темпов роста за одинаковые
отрезки времени по двум рядам динамики) свидетельствует о следующем:
рост фондообеспеченности по сравнению с ростом выхода валовой продукции составлял в относительном выражении 1,26 (1,512:1,204);
рост энергообеспеченности по сравнению с ростом выпуска продукции — 1,09 (1,312:1,204);
Слайд 32 Следовательно, темпы роста факторов интенсивности производства (фондообеспеченость, электрообеспеченность)
опережали темпы роста выхода валовой продукции;
Слайд 33
3. обеспечение одинаковости периодов интервального ряда, по которому
приводятся данные. Так, для характеристики степени ритмичности работы предприятия
данные о производстве продукции по соответствующим декадам сопоставлять нельзя, так как количество рабочих дней отдельных декад могут быть разными, что приводит к отличиям в объемах выпуска продукции.Слайд 34 Например, необходимо построить ряд динамики реализации металлоконструкций по
кварталам года(т):
I II III
IV2340 1820 1380 2024
Для приведения этого ряда к сопоставимому виду определим размер средней дневной реализации продукции с учетом количества дней торговли по кварталам (т):
I — 2340 : 90 = 26;
II— 1820 : 91 = 20;
III— 1380 : 92 = 15;
IV— 2024 : 92 = 22.
Тогда ряд динамики сопоставимых уровней средней дневной реализации хлебобулочных изделий в торговой сети города по кварталам года (т) будет иметь вид:
I II III IV
26 20 15 22
Слайд 35
Показатели рядов динамики
Для оценки свойств динамики в статистике
применяются взаимоувязанные характеристики, или аналитические показатели. Среди них:
абсолютный
прирост; темп роста;
темп прироста;
абсолютное значение одного процента прироста.
Слайд 36
Расчет таких показателей базируется на сопоставлении уровней ряда
уi. Если базой сравнения является начальный (постоянный) уровень ряда
у0, то соответствующие показатели называются базисными, когда база сравнения переменная и отвечает предыдущему уровню уi. то показатели называются цепными.Слайд 37 Абсолютный прирост (или уменьшение) Δi соответствует скорости изменения
уровней и рассчитывается как разность уровней ряда:
а) базисный
б) цепной
где n — количество уровней ряда динамики.
Слайд 38 Цепные и базисные абсолютные приросты связаны между собой
зависимостью (сумма цепных приростов равняется конечному базисному):
Слайд 39 Темп роста Ki. характеризует интенсивность изменений уровней ряда
и выражается относительными величинами в виде коэффициентов или в
процентах:а) базисный
б) цепной
Слайд 41 Темп прироста Тi выражается в процентах и показывает,
на сколько уровень yi. больше (меньше) уровня, взятого за
базу сравнения:а) базисный
б) цепной
Слайд 43 Абсолютное значение одного процента прироста Аi характеризует весомость
каждого процента прироста и рассчитывается как отношение абсолютного прироста
к темпу прироста:Слайд 44 Расчет этого показателя имеет экономический смысл только на
цепной основе, поскольку на базисной основе для всех уровней
будет получено то же значение показателя — сотая часть базисного (первого) уровня.Слайд 45 Абсолютное значение одного процента прироста Аi имеет важное
практическое значение в экономическом анализе; так, в динамических рядах,
уровни которых постоянно растут, темпы роста могут замедляться или оставаться на одном уровне, а значение одного процента прироста расти.Слайд 46 Необходимо отметить, что в динамических характеристиках (коэффициентах или
процентах) непосредственно сравнивать уровни можно путем определения их разности.
Эти разности получили название пунктов роста. Их вычисляют как разность уровней базисных коэффициентов (процентов) темпов роста или прироста двух смежных периодов.Слайд 47 В отличие от темпов прироста, которые нельзя суммировать
и умножить, пункты роста можно складывать, в результате чего
получаем темп прироста соответствующего периода в сравнении с базисным периодом.Слайд 48 В состав аналитических показателей могут быть отнесены коэффициенты
ускорения (замедления) Ky, которые рассчитываются как отношение двух соседних
темпов роста Кi и Кi-1 определенных цепным способомСлайд 49 При сопоставлении в динамике развития двух явлений можно
использовать показатели, которые представляют собой отношение темпов роста или
темпов прироста за одинаковые промежутки времени по двум динамическим рядам. Эти показатели называются коэффициентами опережения Kon:Слайд 51 С помощью этих коэффициентов могут сопоставляться ряды динамики
одинакового содержания, но имеющие отношение к разным территориям (районам,
областям, регионам и т. п.), разным предприятиям (организациям, учреждениям), а также ряды динамики разного содержания, которые характеризуют один и тот же объект.
Слайд 52
Средние показатели рядов динамики
Для нахождения обобщающих характеристик ряда
динамики рассчитывают также средние показатели:
средние уровни динамического ряда;
средние из аналитических показателей.
Слайд 53 Методы вычисления средних уровней динамических рядов зависят от
статистической структуры показателей.
Слайд 54 В интервальном ряду с равными интервалами времени применяют
среднюю арифметическую простую
а для неравных интервалов - среднюю арифметическую
взвешенную:где ti— промежуток времени, в течение которого сохранялось значение уровня уi; n — число уровней ряда.
Слайд 55 В моментных динамических рядах с равными промежутками между
датами средний уровень вычисляется по формуле средней хронологической для
уровнейСлайд 56 Если отрезки времени между датами для моментных рядов
разные, то используют формулу средней арифметической взвешенной:
где
— средние уровни отдельных интервалов времени где ti —длительность соответствующих интервалов
Слайд 57 Если для моментного ряда динамики есть данные только
на начало и конец периода, то средний уровень может
быть рассчитан по формуле:где y1, уn — уровни соответственно на начало и конец периода
Слайд 58
К средним из аналитических показателей относятся:
средний абсолютный прирост;
средний темп роста;
средний темп прироста.
Слайд 59 Средний абсолютный прирост характеризует среднюю скорость роста (или
уменьшения) п уровней ряда динамики. Для моментных и интервальных
рядов средний абсолютный прирост вычисляется по формуле:где т — число цепных абсолютных приростов (m = п -1).
Слайд 60 Средний темп роста показывает, во сколько раз в
среднем каждый данный уровень больше (или меньше) предыдущего уровня.
Для рядов динамики с равными интервалами средний темп роста рассчитывается по формуле средней геометрической:где Кi — темп роста за отдельные периоды времени; т — число цепных темпов роста (т=п-1).
Слайд 61
Эту формулу можно записать иначе, если учесть, что
где
у0, уm — начальный и конечный уровни ряда динамики
Слайд 62 На основе среднего темпа роста определяет средний темп
прироста , который показывает, на сколько процентов в среднем
увеличивается (уменьшается) этот уровень по сравнению с предыдущим. Его вычисляют по формуле:
Слайд 63
ВЫВОД
Для всесторонней характеристики изменения социально-экономических явлений во времени
определение только показателей динамики и их средних величин недостаточно.
В связи с этим статистика рекомендует ряд специальных приемов обработки и анализа рядов динамики.
Слайд 64
Методы обработки динамических рядов
При анализе рядов динамики
важно выявить общую тенденцию развития (тренд) социально-экономического явления, то
есть установить в каком направлении (рост, спад) и по какой зависимости (линейной или нелинейной) оно изменяется. Эта задача в статистке называется выравниванием динамических рядов.Слайд 65 Часто уровни ряда со временем изменяются (колеблются), но
это изменение для разных явлений неодинаково и может быть
вызвано разными причинами. Динамика ряда включает три компоненты:тенденцию (или долговременное движение);
кратковременное систематическое движение;
несистематическое случайное движение.
Слайд 66 Изучая ряды динамики, исследователи пытаются выявить главным образом
общую тенденцию (тренд) в изменениях уровней ряда, то есть
основную закономерность развития явления. Для этого ряды динамики подлежат специальной обработке — выравниванию.Она позволяет характеризовать особенности изменения по времени динамического ряда в наиболее общем виде, считая, что через фактор времени можно передать влияние всех главных факторов.
Слайд 67 К способам и методам выравнивания динамических рядов могут
быть отнесены такие:
а) увеличение интервалов;
б) вычисление средних уровней для
увеличенных интервалах;в) определение скользящей (подвижной) средней;
г) аналитическое выравнивание.
Слайд 68 Наиболее простым способом выравнивания динамических рядов является увеличение
их интервалов.
Суть этого подхода заключается в том, что
первоначальный ряд динамики заменяется другим, уровни которого относятся к большим по продолжительности периодам времени (дневные интервалы заменяются на пяти- или десятидневные, месячные интервалы — квартальными и т. п.). Слайд 69 Вновь образованный ряд будет содержать увеличенные уровни, которые
получены суммированием уровней первоначального ряда. При этом отклонения в
уровнях, обусловленных случайными причинами, взаимно гасятся, сглаживаются, и более явно проявляется действие основных факторов изменения уровней, то есть выявляется общая тенденция.
Слайд 70
Пример
Даны сведения об объеме реализации продукции помесячно
Январь
366
Февраль 310
Март 296
Апрель 380
Май 336
Июнь 295
Июль 380
Август 381
Сентябрь 392
Октябрь 444
Ноябрь 382
Декабрь 398
Слайд 71 Разные направления изменений по отдельным месяцам уровней данного
ряда динамики затрудняют выводы об основной тенденции продажи продукции.
Решение
этой задачи упрощается, если соответствующие месячные уровни соединить в квартальные: I квартал – 972 шт.,
II квартал – 1011шт.,
III квартал – 1153 шт.,
IVквартал -1224 шт.
Слайд 72 После увеличения интервалов основная тенденция роста продаж продукции
становится явной:
972 < 1011 < 1153 < 1224.
Слайд 73 Частным случаем рассмотренного способа является вычисление средних уровней
для увеличенных интервалов. При этом увеличенные уровни ряда динамики
заменяются средними уровнями для увеличенных интервалов.Слайд 74 Одним из распространенных методов выравнивания динамических рядов является
их сглаживание с помощью скользящей средней.
Сущность метода заключается
в том, что для первоначального ряда динамики формируются увеличенные интервалы, которые состоят из одинакового количества уровней т. Слайд 75 Таким образом, каждый последующий интервал получается смещением от
начального на один уровень.
Тогда для новых интервалов рассчитываются
средние уровни: и т.д.
которые как бы «сглаживают» уровни и «текут» по динамическому ряду с шагом, равным единице.
Слайд 76 Получается новый ряд, составленный из скользящих средних. Каждая
из средних относится к середине укрупненного интервала, поэтому технически
удобнее составлять увеличенные интервалы из нечетного количества уровней т (три, пять, семь и т. п.).Слайд 77 Нахождение скользящей средней для четного количества уровней представляет
неудобство, обусловленное тем, что средняя может находиться между двумя
уровнями и поэтому необходима дополнительная процедура — центрирование: вычисление средней из двух смежных средних для каждого интервала.Слайд 78 В результате новый динамический ряд, построенный из скользящих
средних, дает выраженную тенденцию развития явления за счет устранения
колебаний уровней в результате случайных причин. Это наглядно проявляется при графическом изображении фактических и сглаженных данных при выявлении тенденции развития явления (увеличения или уменьшения по времени).
Слайд 79
Пример
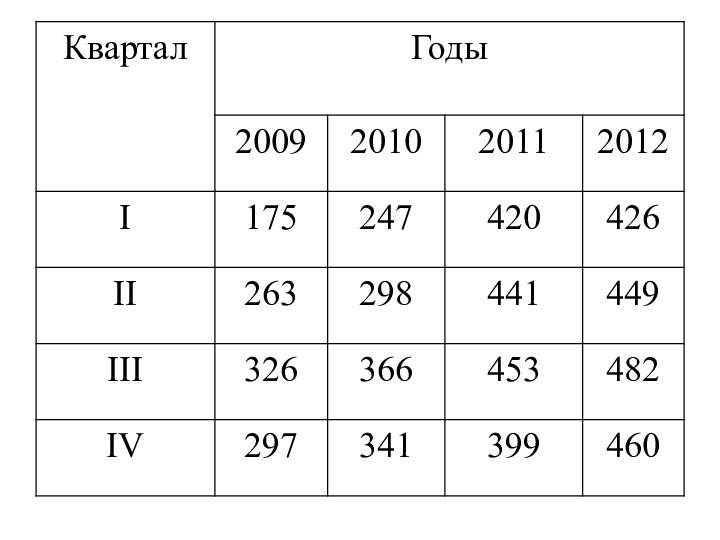
Использование этого метода рассмотрим по данным о реализации
продуктов питания в магазинах города (тыс. д. е.). Соответствующие
исходные данные сведены в таблицуСлайд 81 Особенностью данных табл. является периодическое изменение квартальных уровней:
увеличение продажи в II и III кварталах и снижение
в IV квартале. Основная тенденция здесь не просматривается.Слайд 82 Для выявления тенденции развития методом скользящей средней количество
уровней первоначального ряда объединяются в увеличенные интервалы. Обычно для
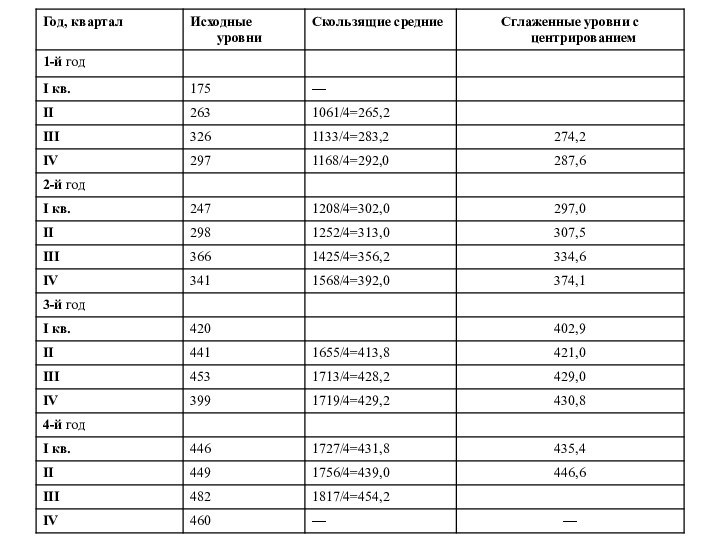
характеристики развития товарооборота магазинов по годам сопоставляются интервалы из четырех годовых кварталов.Слайд 83 Поэтому при использовании метода скользящих средних их расчет
заключается в определении средних величин из четырех уровней ряда
с отбрасыванием при расчете каждой новой скользящей средней одного уровня слева и присоединение одного уровня справа:В нашем примере рассчитывается 13 скользящих средних
Слайд 86 Для четного числа уровней каждое значение скользящей средней
приходится на промежуток между двумя смежными кварталами.
Так, первая
скользящая средняя (265,2) лежит между кварталами II и III, другая (283,2) — между кварталами III и IV и т. д. Слайд 87 Для нахождения сглаженных уровней выполняется центрирование (графа 4).
Для III квартала рассчитывается среднее значение между первой и
второй скользящими средними:(265,2+283,2)/2=274,2 тыс. д. е.;
для IV квартала центрируется вторая и третья скользящие средние:
(283,2+292,0)/2=287,6 тыс. д. е. и т. д.
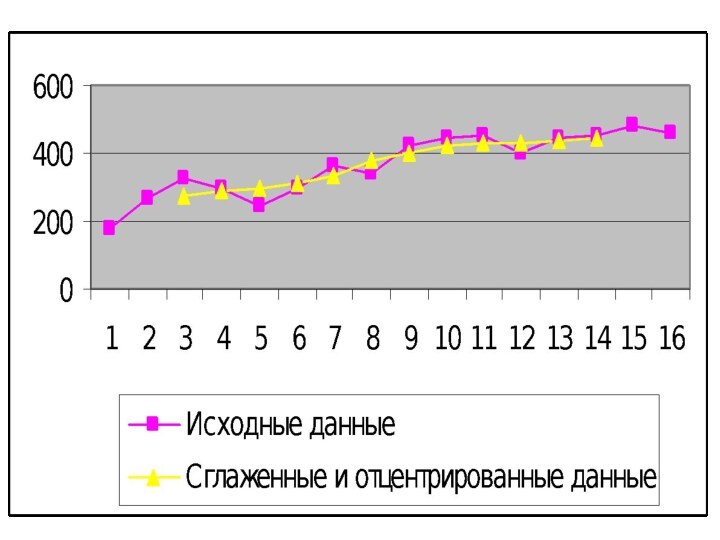
Слайд 88 Полученные данные сглаженных уровней находятся в гр. 4.
Их графическое изображение показывает тенденцию развития торговли магазинами города
с использованием метода скользящей средней .Слайд 89 Недостатком выровненного ряда методом скользящей средней является то,
что такой ряд «сокращается» по сравнению c первоначальным на (n-1)/2
уровней ряда с одного и второго концапод n понимают количество уровней первоначального ряда, по которым определяют скользящие средние.
Слайд 90 Использование в анализе рядов динамики способа увеличения интервалов
и метода скользящей средней позволяет выявить тренд для его
описания, но получить обобщающую статистическую оценку тренда этими подходами невозможно. Решение задачи — измерение тренда — достигается методом аналитического выравнивания.Слайд 91 Сущность аналитического выравнивания динамического ряда заключается в том,
что фактические уровни ряда заменяются плавными уровнями, вычисленными на
основе определенной линии (прямой или кривой), выбранной в предположении, что она точнее всего отображает общую тенденцию явления.Слайд 92 В основе метода лежит установление функциональной зависимости уровней
ряда от времени Yt = f( t) с использованием
корреляционно-регрессионного анализа, который описан в курсе эконометрики.
Слайд 93
При этом на практике чаще всего применяются математические
функции такого вида:
а) линейнаяYt = а9 + а1t
б) параболическая
;
Слайд 94
в) гиперболическая
г) степенная
где а9 , а1 –параметры, которые находят методом наименьших квадратов; t – порядковый номер периода.
Слайд 95
На основе теоретического анализа выявляется характер развития явления
во времени, и на этой основе выбирается тот или
другой вид аналитической функции. Практикой статистических исследований установлено, что принятие соответствующей аналитической функции осуществляется при таких условиях:Слайд 96 выравнивать динамические ряды по уравнению прямой линии целесообразно
тогда, когда более или менее постоянны цепные абсолютные приросты, то
есть тогда, когда уровни ряда пзменяются приблизительно в арифметической прогрессии;Слайд 97 выравнивание динамических рядов по уравнению квадратичной параболы необходимо
выполнять в тех случаях, когда изменение уровней ряда происходит с
приблизительно равномерным ускорением или замедлением цепных абсолютных приростов;Слайд 98 выравнивание по степенной функции целесообразно использовать тогда, когда
уровни ряда динамики выявляют тенденцию постоянства цепных темпов роста,
то есть в случае изменения уровней ряда динамики в геометрической прогрессии.Слайд 99 В практической деятельности может возникнуть необходимость интерполяции или
экстраполяции рядов динамики. Самым совершенным при этом является выравнивание
их по определенному аналитическому уравнению.Слайд 100 Интерполяция — это нахождение отсутствующих промежуточных уровней ряда.
Зная уравнение тренда для вычисления теоретических уровней и подставляя
в него промежуточные значения t между заданными, можно определить отвечающий им теоретический уровень результативного фактора .Слайд 101 Экстраполяция используется при прогнозировании общественных явлений в будущем
с предположением, что выявленная тенденция будет сохраняться и в
дальнейшем за пределами исследуемого ряда динамики. При этом значения t вне пределов динамического ряда подставляют в трендовое уравнение и получают точечное прогнозное значение уровня тренда Yпр будущем.Слайд 102 На практике результат экстраполяции прогнозируемых уровней социально-экономических явлений
обычно выполняют интервальными оценками. Для определения границ интервалов используется
интервальное неравенство:Слайд 103 где tg — коэффициент доверия t- распределения Стьюдента;
– остаточное среднее квадратическое отклонение
п — количество уровней рассматриваемого (базисного) ряда динамики;
т — количество параметров теоретической зависимости тренда;
(п-т) — число степеней свободы;
Уt — дискретное (точечное) значение прогнозного уровня.
Слайд 104 Коэффициент доверия tg выбирается из статистических таблиц распределения
Стьюдента в зависимости от числа степеней свободы (n -
т) и уровня значимости (0,01 или 0,05).
Слайд 105
Тогда окончательно с вероятностью
P=1 — α
прогнозный
уровень тренда в будущем Yt будет находиться в пределах:
верхний предел составляет
нижний предел — .