- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Символическая логика
Содержание
- 2. Символическая логикаона же символическаяформируется в XIX веке,
- 4. Логика высказываний
- 5. Высказываниемысль, выраженная повествовательным предложением, которая может быть истинной или ложной
- 6. Формальный аппаратА, В, С…. – пропозициональные переменные
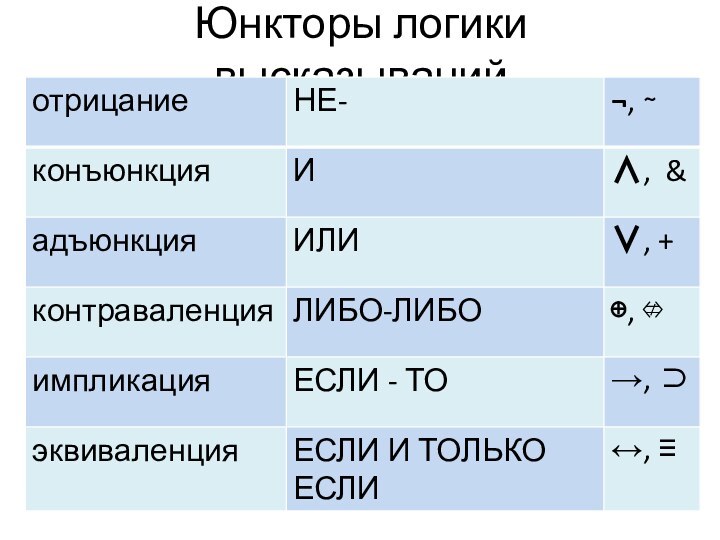
- 7. Юнкторы логики высказываний
- 8. Преобразование конъюнкции в дизъюнкцию(А В) =
- 9. Преобразование дизъюнкции в конъюнкцию(А В) =
- 10. Преобразование импликации в конъюнкцию(А → В) =
- 11. Преобразование строгой дизъюнкции в конъюнкцию(А В) = (А В) (А В)
- 13. Правило подстановкилюбую буквенную переменную в символическом выражении
- 14. Законы символической логики
- 15. Закон ассоциативности(А (В С)) =
- 16. Закон дистрибутивностидля двух переменных(А (В
- 17. Закон двойственностидля конъюнкции и дизъюнкции(А В)
- 18. Закон контрапозиции(А → В) = (А →
- 19. Закон транспозиции((А В) → С) =
- 20. Закон поглощения(А (А В)) =
- 21. результат реконструкции естественного языкаЗдесь есть точные правила
- 23. Именаобозначают отдельный объект, бывают простые и сложные.
- 24. Предметные функторызнаки так называемых предметных функций (функциональная
- 25. Предикатор(предикатная константа)- выражение языка (слова и словосочетания),
- 26. Язык логики предикатов
- 27. Определение терма
- 28. Примера – «Аполлон» в – «Венера» f1
- 29. Определение формулы
- 30. Область действия квантораЕсли формула А имеет вид
- 31. Пример«Если целое число больше 13, то его
- 32. Некоторые законы логики предикатов1. Взаимовыразимость кванторовхА
- 33. Некоторые законы логики предикатов4. Законы пронесения и
- 34. Примеры«Все люди интересуются строением космоса»,х(Р1(х) Q1(х,
- 35. Исчисление естественного выводапорождение одних формул из другихЗдесь нет аксиом. Знание не истинное, а доказуемое.
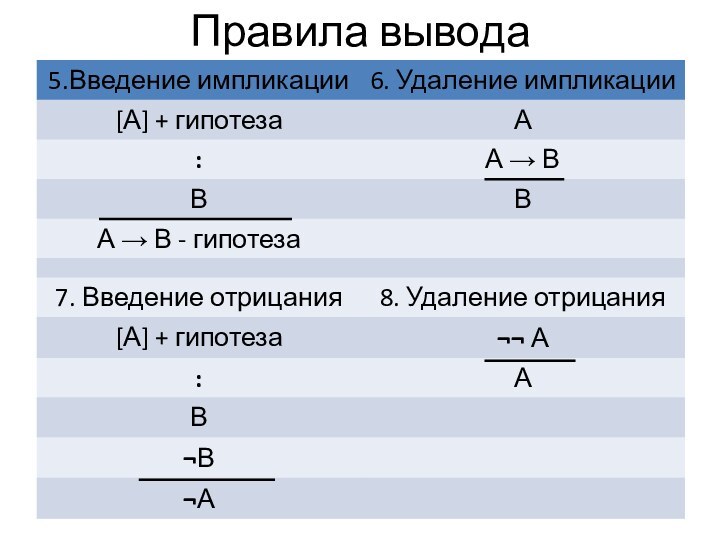
- 36. Правила вывода
- 37. Правила вывода
- 38. Пример«Семён сидит дома или разговаривает по телефону.
- 39. Скачать презентацию
- 40. Похожие презентации
Символическая логикаона же символическаяформируется в XIX веке, благодаря Готлобу Фреге и Бертрану Расселусостоит в обширном использовании символов для привычных логических форм, которые делают логическое рассуждение более сжатым и наглядным



































Слайд 2
Символическая логика
она же символическая
формируется в XIX веке,
благодаря
Готлобу Фреге и Бертрану Расселу
для привычных логических форм, которые делают логическое рассуждение более сжатым и наглядным
Слайд 5
Высказывание
мысль, выраженная повествовательным предложением, которая может быть истинной
или ложной
Слайд 6
Формальный аппарат
А, В, С…. – пропозициональные переменные (формулы),
отражающие независимый факт;
– униарная связка-юнктор;
, ,
… – бинарные связки-юнкторы;() – технические знаки;
(А В), ( А)…. – формулы.
Слайд 13
Правило подстановки
любую буквенную переменную в символическом выражении можно
заменять на произвольную формулу
Например,
(p p)
p = (a ↔
b)((a ↔ b) (a ↔ b))
Слайд 15
Закон ассоциативности
(А (В С)) = ((А
В) С)
(А (В С))
= (А В) С) Закон коммутативности
(А В) = (В А)
(А В) = (В А)
Слайд 16
Закон дистрибутивности
для двух переменных
(А (В С))
= (А В) (А С)
(А
(В С)) = (А В) (А С) для большего количества переменных
(А В) (С D) = (А C) (А D) (B C) (B D)
(А В) (C D) = (А C) (А D) (B C) (B D)
Слайд 17
Закон двойственности
для конъюнкции и дизъюнкции
(А В) =
(А В)
(А В) = (А В)
для
эквивалентности и строгой дизъюнкции(А ↔ В) = ( В А)
(А В) = ( В ↔ А)
Слайд 18
Закон контрапозиции
(А → В) = (А → В)
((А
В) → С) = (С →(А В))
Закон импортации
(А
→ (В → С)) = ((А В) → С) Закон экспортации
((А В) → С) = (А → (В → С))
Слайд 20
Закон поглощения
(А (А В)) = А
(А
(А В)) = А
Закон выявления
(А С)
(В С) = (А С) (В С) (А В) (А С) (В С) = (А С) (В С) (А В)
Слайд 21
результат реконструкции естественного языка
Здесь есть точные правила построения
высказываний (формул)
и сложных имен (термов)
Этот язык предназначен для
аксиоматического построения теорий, для анализа содержания высказываний естественного языка и выявления логических отношений между ними, для описания правил рассуждения, построения выводов и доказательствЛогика предикатов
Слайд 23
Имена
обозначают отдельный объект, бывают простые и сложные.
Простые
не содержат никакой информации об обозначаемых индивидах (имена собственные).
Сложные имена не только обозначают предмет, но и указывают на какие-либо его свойства
Слайд 24
Предметные функторы
знаки так называемых предметных функций (функциональная константа)
Наряду
с математическими функциями «синус», «логарифм», «умножение» и т.п. сюда
относятся такие особые характеристики предметов, как скорость, плотность, возраст, пол, профессия, агрегатное состояние, место жительства и др.
Слайд 25
Предикатор
(предикатная константа)
- выражение языка (слова и словосочетания), предметными
значениями которого являются свойства (одноместные предикаторы) или отношения (многоместные
предикаторы)
Слайд 28
Пример
а – «Аполлон»
в – «Венера»
f1 –
«красавец»
g2 – «молодой»
f1(a) – Аполлон – красавец.
g2(a,в)
– Аполлон и Венера – молоды. g2(f1(a),в) – Красавец Аполлон и Венера – молоды.
f1(g2(a,в)) – Красавцы, молодые Аполлон и Венера.
Слайд 30
Область действия квантора
Если формула А имеет вид хВ
или хВ, то областью действия квантора или
по переменной х является формула В
Слайд 31
Пример
«Если целое число больше 13, то его квадрат
делится без остатка на 4 или на 5»
х((Рх
Q2(х, 13)) (R(g(х, х), 4) R (g(х, х), 5)), где
Р - «быть целым числом»,
Q2 - «больше чем»,
R - «делится на»
Слайд 32
Некоторые законы логики предикатов
1. Взаимовыразимость кванторов
хА хА,
хА
хА.
2. Отрицание кванторов
хА хА,
хА хА.
3. Перестановка
кванторовxyА yxА,
xyА yxА,
xyА yxА.
Слайд 33
Некоторые законы логики предикатов
4. Законы пронесения и вынесения
кванторов
а) конъюнкция
a(А В) (aА aВ);,
a(А
В) (aА aВ), б) дизъюнкция
a(А В) (aА aВ),
(aА aВ) a(А В),
в) импликация
a(А В) (aА aВ),
(aА aВ) a(А В).
Слайд 34
Примеры
«Все люди интересуются строением космоса»,
х(Р1(х) Q1(х, f(a))
где
Р1 – «быть человеком», Q1 – «интересоваться», f –
«строение …», a – «космос»«Некоторые звёзды не видны невооружённым глазом, но видны в телескоп»
х(Р2(х) уz((Р3(у) Р4(z)) (Q2(х, y) Q2(х, z))))
где Р2 – «быть звездой», Р3 – «быть невооружённым органом зрения», Р4 – «быть телескопом», Q2 – «виден с помощью»