- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Содержание:
Содержание
- 2. Содержание:Связь между алгеброй логики и двоичным кодированиемЛогические высказыванияОперации над высказываниямиАлгебра высказыванийАлгебра логикиОсновные законы логики
- 3. 1666 год - немецкий ученый Лейбниц попытался
- 4. Понятие высказыванияПростое высказывание –некоторое повествовательное предложение, которое
- 5. Тождественная истина и тождественная ложьФормула А, всегда
- 6. Операции над высказываниямиДизъюнкция VКонъюнкция &Отрицание aИмпликация
- 7. Дизъюнкция a V b (логическое сложение) Запись
- 8. Конъюнкция a&b (логическое умножение) Запись читается «а
- 9. Отрицание (инверсия ┐) Запись читается «не
- 10. Импликация a b Запись читается «а импликация
- 11. Эквивалентность a b Запись читается «а
- 12. Жегалкинское сложение a b Запись читается
- 13. Алгебры для работы с высказываниями Используются две алгебры для работы над высказываниями
- 14. Алгебра высказыванийОперации дизъюнкция, конъюнкция, отрицание, импликация и эквивалентность составляют сигнатуру алгебры высказываний
- 15. Алгебра Буля (алгебра логики)Алгебраическая система, содержащая в
- 16. Логические функцииВ алгебре высказываний и алгебре логики
- 17. Порядок выполнения логических операцийИнверсия - ┐Конъюнкция -
- 18. Построение таблицы сложного выражения
- 19. Таблица истинности сложного выражения
- 20. Построить таблицу истинности для формулы F( x1,
- 21. Дана функция f(x,
- 22. Основные законы логикиЗакон идемпотентности: А ٨ А=
- 23. Дистрибутивность (распределение): Умножения относительно сложения:(А۷В) ٨ С
- 24. Законы де Моргана:¬(А٨В)= ¬А۷¬В¬ (А۷В) = ¬А
- 25. ¬ (А۷В) = ¬А ٨¬В¬(А٨В)= ¬А۷¬ВЗаконы де Моргана
- 26. Формализация логических высказываний
- 27. Формализация логических высказыванийabВетрено бывает тогда и только
- 28. Алгоритм формализации высказыванийвыделить из составного высказывания простые
- 29. Представление логических функциональных элементов· единицей 1,
- 30. Представление элементов
- 31. Метод построения логических схемПостроим таблицу истинности для
- 32. Пример 1Построить схему для функции f(x1, x2,
- 33. Пример 1МДНФ = x1x2 x4 + x1x3
- 35. Скачать презентацию
- 36. Похожие презентации
Содержание:Связь между алгеброй логики и двоичным кодированиемЛогические высказыванияОперации над высказываниямиАлгебра высказыванийАлгебра логикиОсновные законы логики






















Слайд 2
Содержание:
Связь между алгеброй логики и двоичным кодированием
Логические высказывания
Операции
над высказываниями
Слайд 3 1666 год - немецкий ученый Лейбниц попытался перевести
законы мышления (формальную логику) из словесных форм, полных неопределенностей,
в математику, где отношения между объектами или высказываниями определяются в виде математических соотношений.В 1847 год- Буль написал статью на тему «Математический анализ логики»
В 1854 году Буль развил свои идеи в работе «Исследование законов мышления»
Связь между алгеброй логики и двоичным кодированием.
Математический аппарат алгебры логики удобен для описания функционирования аппаратных средств компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, значений логических переменных тоже : “1” и “0”
Историческая справка
Слайд 4
Понятие высказывания
Простое высказывание –некоторое повествовательное предложение, которое может
быть либо истинно, либо ложно, но не то и
другое одновременноОбозначается маленькими латинскими буквами a, b, c, …
Высказывания, получаемые из простых с помощью грамматических связок «и», «или», «не», «тогда и только тогда», «либо…либо…», «если …то…» называются составными или формулами
Обозначаются большими латинскими буквами A, B, C, …
.
Слайд 5
Тождественная истина и тождественная ложь
Формула А, всегда истинная,
называется тождественно истинной формулой или тавтологией, А=1
Формула В, всегда
ложная, называется тождественно ложной формулой, В=0Рассматривая высказывания, мы абстрагируемся от их смысла, нас интересует их истинность или ложность
.
Слайд 6
Операции над высказываниями
Дизъюнкция V
Конъюнкция &
Отрицание a
Импликация
Эквивалентность
Жегалкинское сложение
Значение каждой логической
операции описывается таблицей истинности
Слайд 7
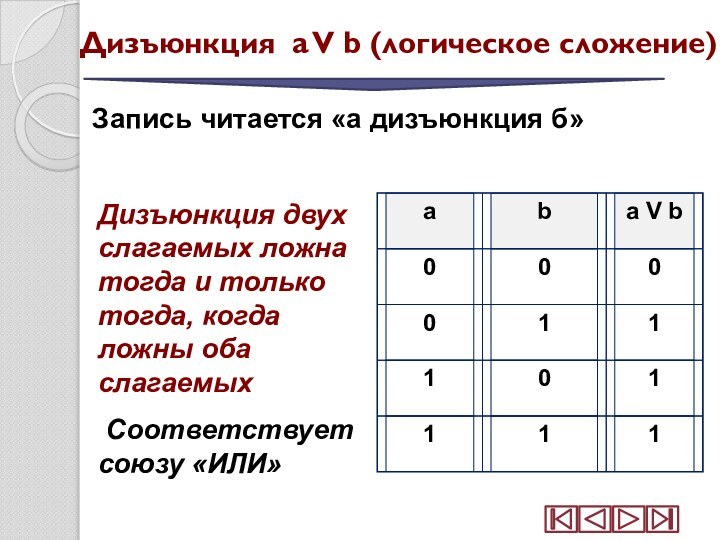
Дизъюнкция a V b (логическое сложение)
Запись
читается «а дизъюнкция б»
Дизъюнкция двух слагаемых ложна тогда
и только тогда, когда ложны оба слагаемыхСоответствует союзу «ИЛИ»
Слайд 8
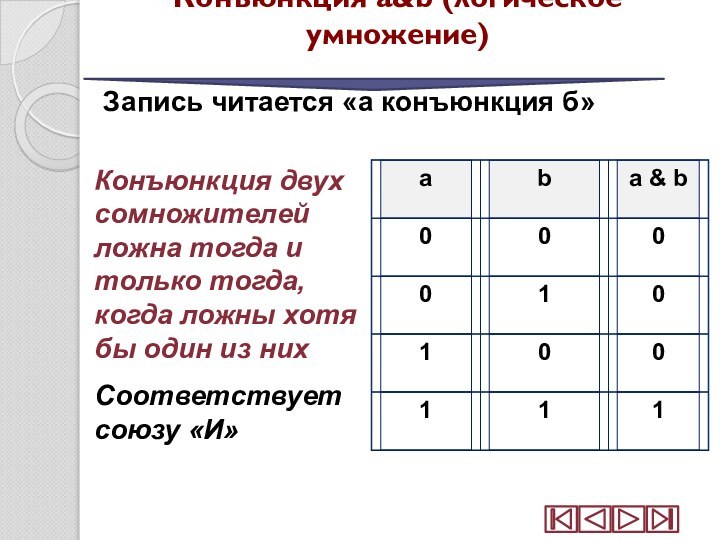
Конъюнкция a&b (логическое умножение)
Запись читается «а конъюнкция
б»
Конъюнкция двух сомножителей ложна тогда и только тогда,
когда ложны хотя бы один из них Соответствует союзу «И»
Слайд 9
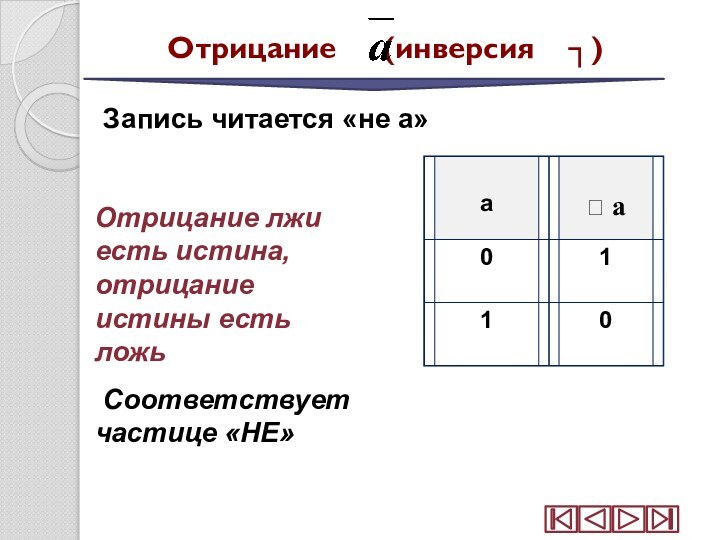
Отрицание (инверсия ┐)
Запись читается «не а»
Отрицание лжи есть истина, отрицание истины есть ложь
Соответствует частице «НЕ»
Слайд 10
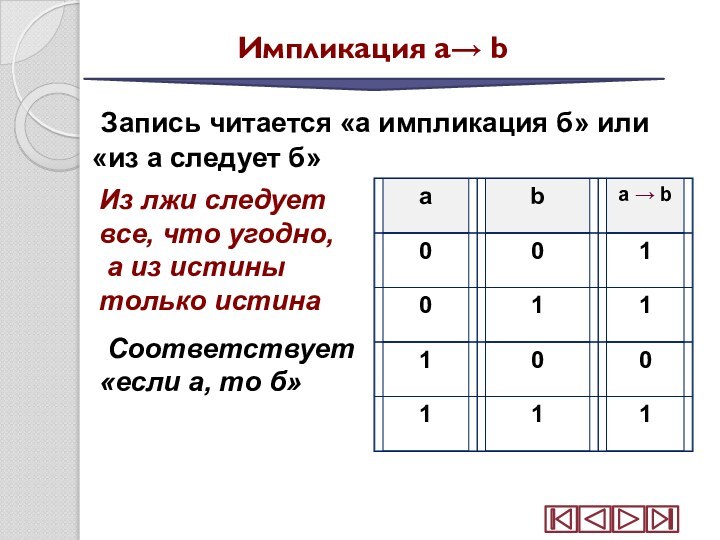
Импликация a b
Запись читается «а импликация
б» или «из а следует б»
Из лжи следует
все, что угодно,а из истины только истина
Соответствует «если а, то б»
Слайд 11
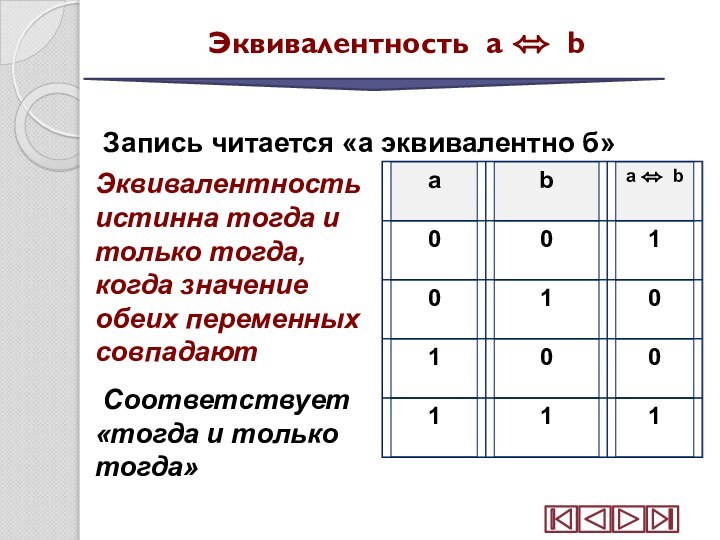
Эквивалентность a b
Запись читается «а
эквивалентно б»
Эквивалентность истинна тогда и только тогда, когда
значение обеих переменных совпадаютСоответствует «тогда и только тогда»
Слайд 12
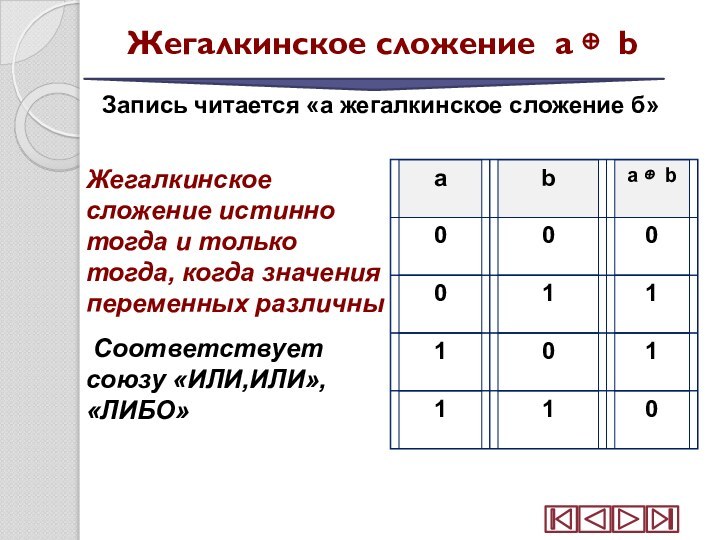
Жегалкинское сложение a b
Запись читается
«а жегалкинское сложение б»
Жегалкинское сложение истинно тогда и
только тогда, когда значения переменных различны Соответствует союзу «ИЛИ,ИЛИ», «ЛИБО»
Слайд 14
Алгебра высказываний
Операции дизъюнкция, конъюнкция, отрицание, импликация и эквивалентность
составляют сигнатуру алгебры высказываний
Слайд 15
Алгебра Буля (алгебра логики)
Алгебраическая система, содержащая в качестве
сигнатуры логическое умножение, логическое сложение и отрицание, которые позволяет
производить тождественные преобразования логических выражений, и множество {0, 1} в качестве носителя, называется алгеброй Буля (алгеброй логики)Aб= <{0, 1} ,+, ->
.
Слайд 16
Логические функции
В алгебре высказываний и алгебре логики используются
только логические переменные, которые принимают значения либо 0 (ложь),
либо 1 (истина)Функции, которые определены на этих переменных и принимают значения 0 или 1, также называются логическими, или булевыми
Слайд 17
Порядок выполнения логических операций
Инверсия - ┐
Конъюнкция - &
или ٨
Дизъюнкция – ۷
Импликация –
Эквивалентность -
Для изменения порядка выполнения логических операций используются круглые скобки.Например: D = ┐( A ۷ B ٨ C)
Слайд 18
Построение таблицы сложного выражения
Пример
построения таблицы истинности для сложного (составного) логического выражения:
D = ┐A ٨ (B ۷ C)Необходимо спланировать таблицу, то есть установить число строк и столбцов таблицы
При определении числа строк необходимо перебрать все возможные сочетания логических значений 0 и 1 исходных выражений А, В и С, из которых формируется заданное сложное логическое выражение
При добавлении третьего аргумента записываются первые 4 строки таблицы, сочетания с значением третьего аргумента равным 0 , а затем записываются эти же 4 строки, но с значением третьего аргумента, равным 1
Для трех аргументов в таблице оказывается 8 строк
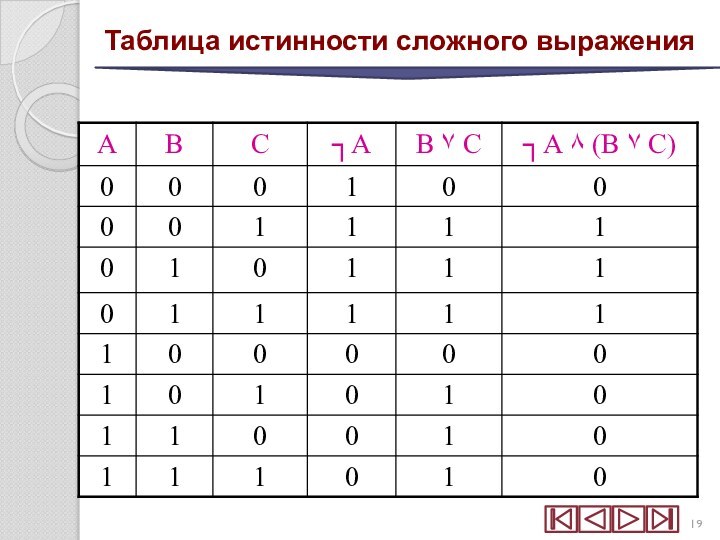
Слайд 20
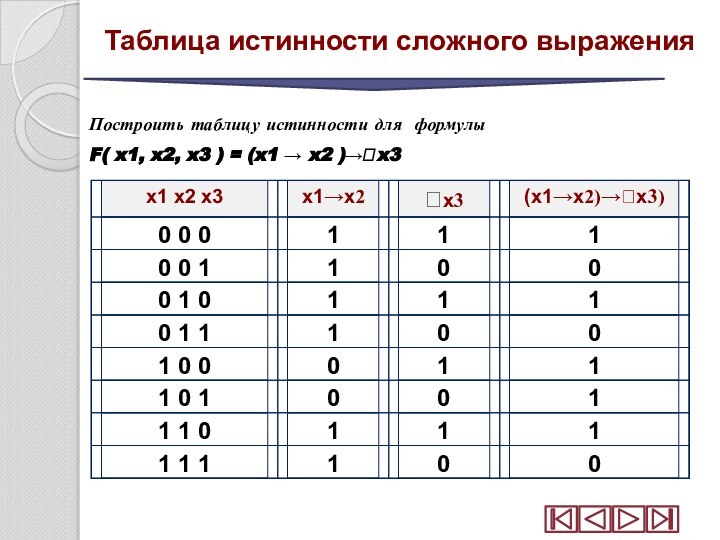
Построить таблицу истинности для формулы
F( x1, x2,
x3 ) = (x1 x2 )x3
Таблица истинности
сложного выражения
Слайд 21
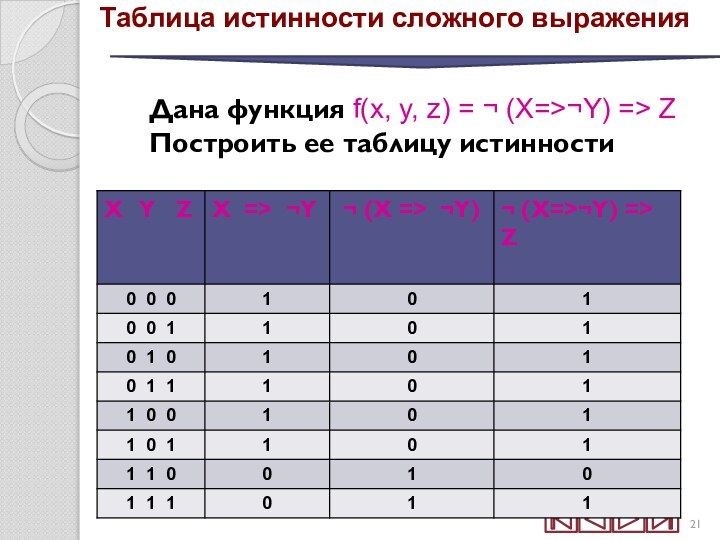
Дана функция f(x, y,
z) = ¬ (X=>¬Y) => Z
Построить ее таблицу истинностиТаблица истинности сложного выражения
Слайд 22
Основные законы логики
Закон идемпотентности: А ٨ А= А;
А ۷ А= А
Двойное отрицание (инволюция): ¬(¬А) = А
Закон
исключения третьего: А۷¬ А=1 (всегда истина)Закон противоречия: А ٨ ¬ А= 0 (всегда ложь)
Закон коммутативности:
А۷ В= В ۷ А; А ٨ В = В ٨ А
Закон ассоциативности:
(А۷В) ۷ С = А ۷ (В۷С); (А٨В) ٨ С = А ٨ (В٨С)
Слайд 23
Дистрибутивность (распределение):
Умножения относительно сложения:
(А۷В) ٨ С =
(А٨С) ۷ (В٨С)
и наоборот:
(А٨В) ۷ (В٨С) =
В ٨ (А۷С)Сложения относительно умножения:
А۷В٨С = (А۷В) ٨ (А۷С)
Основные законы логики(продолжение)
Слайд 24
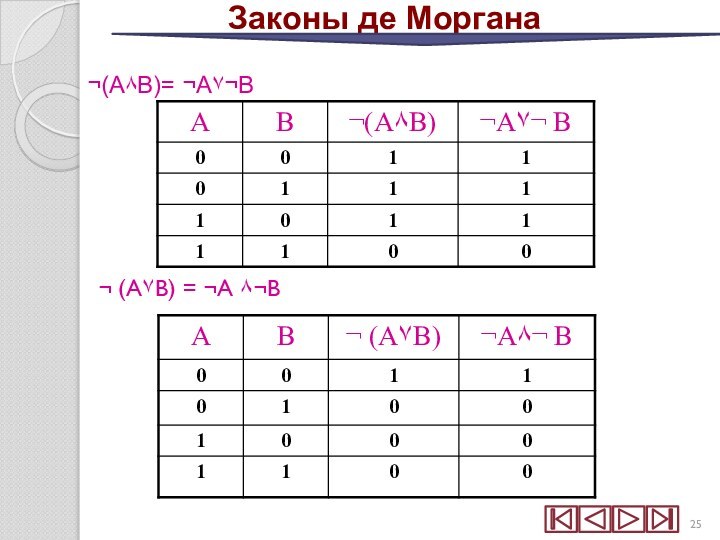
Законы де Моргана:
¬(А٨В)= ¬А۷¬В
¬ (А۷В) = ¬А ٨¬В
Законы
работы с константами 0 и 1:
А۷1 = 1 0۷1
= 1 А٨1 = А 0٨1 = 0
А٨0 = 0
В ٨ 1= В
Основные законы логики(продолжение)
Слайд 27
Формализация логических высказываний
ab
Ветрено бывает тогда и только тогда,
когда идет дождь
b a
а тогда и только тогда,
когда б
Слайд 28
Алгоритм формализации высказываний
выделить из составного высказывания простые высказывания
и обозначить их латинскими буквами
построить дерево синтаксического разбора, в
котором каждой вершине соответствует логическая связка (операция), а концевым вершинам – простые высказываниязаписать логическую формулу путем обхода дерева с учетом структуры дерева и старшинства логических операций
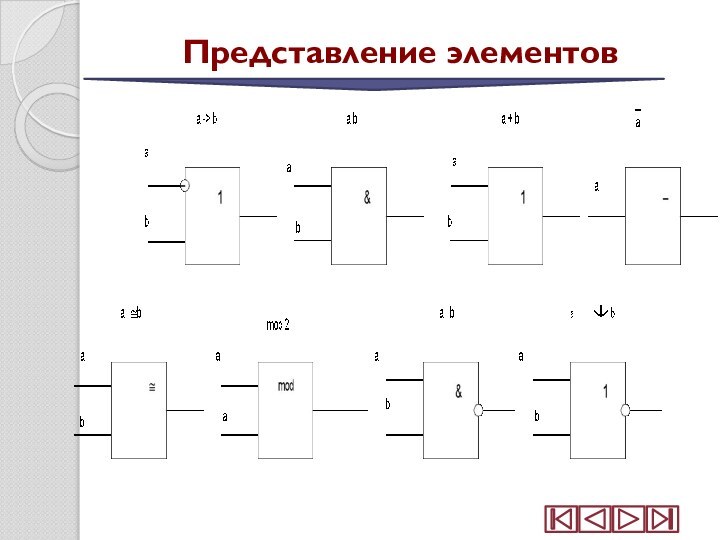
Слайд 29
Представление логических
функциональных элементов
· единицей 1, если он
реализует логическое сложение
· знаком конъюнкции «&», если реализует логическое умножение
·
М2, если соответствует сложению по модулю два (жегалкинскому сложению)· «», если реализует функцию эквивалентности
.
Слайд 31
Метод построения логических схем
Построим таблицу истинности для рассматриваемой
функции
Построим совершенную ДНФ (т.е. логическую сумму наборов, на которых
функция задана как истинная)Упростим СовДНФ с помощью законов алгебры логики
Приведем функцию к виду, удобному для реализации в заданном базисе
Проведем анализ функции и построим схему из функциональных элементов
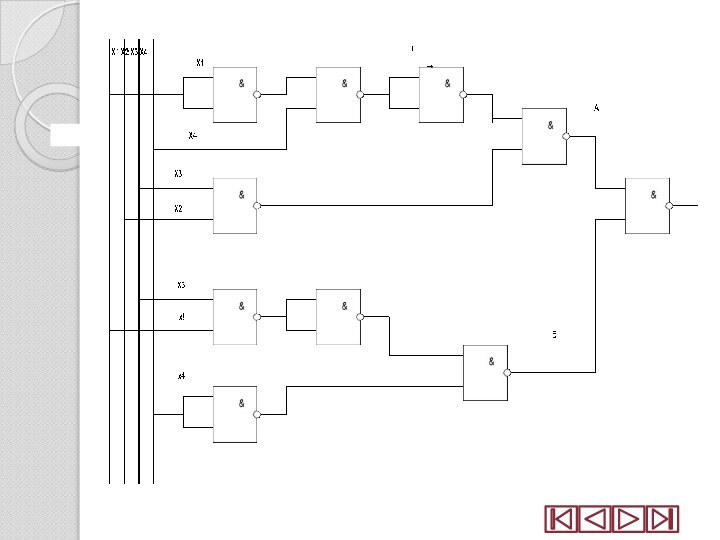
Слайд 32
Пример 1
Построить схему для функции
f(x1, x2, x3,
x4), истинной на наборах
1, 3, 5, 10 и
14 на функциональных элементах И - НЕ СДНФ =





























