Слайд 2
Логические представления – описание системы, процесса или явления
в виде совокупности сложных высказываний, составленных из простых (элементарных)
высказываний и логических связок между ними.
Логические представления и их составляющие характеризуются определёнными свойствами и набором допустимых преобразований, реализующих правильные методы рассуждений – законы логики, разработанные в формальной (математической) логике.
Слайд 3
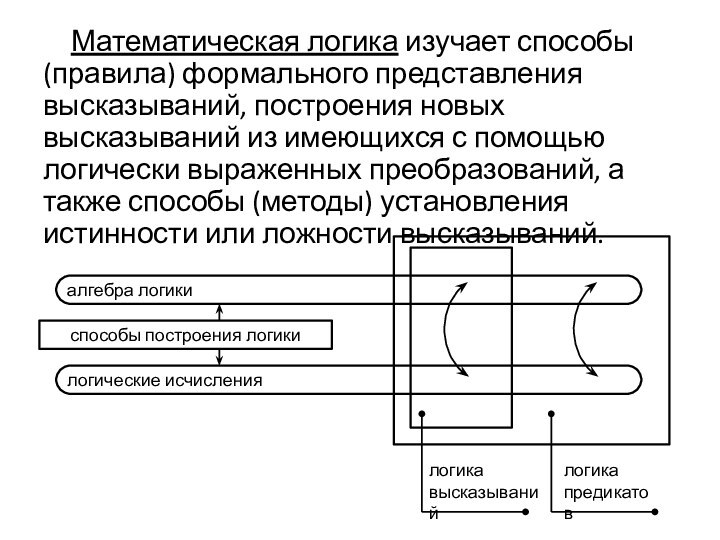
Математическая логика изучает способы (правила) формального представления высказываний,
построения новых высказываний из имеющихся с помощью логически выраженных
преобразований, а также способы (методы) установления истинности или ложности высказываний.
алгебра логики
логические исчисления
способы построения логики
логика
высказываний
логика
предикатов
Слайд 4
Основными объектами разделов логики являются высказывания.
Высказывание – последовательное
предложение (утверждение, суждение), о котором можно говорить, что оно
истинно или ложно. Для того, чтобы оперировать высказываниями, необходимо знать их истинное значение (истинность).
Слайд 5
4.1. Основные понятия.
Простое (элементарное) высказывание – рассматривается как
неделимое целое. Обычно это высказывания не содержащие логических связок.
Сложное
(составное) высказывание – составляется из простых с помощью логических связок.
«и», «или», «не», «если … то …»,
«либо … либо …» (в разделительном смысле), «тогда и только тогда»
и др.
Слайд 6
Основные логические связки (операции) логики высказываний:
Конъюнкция (операция «И»,
логическое произведение)
- P&Q, P∧Q, P∙Q
- «P и Q»
Дизъюнкция (операция
«ИЛИ», логическая сумма)
-P∨Q, P+Q
- «P или Q»
- понимается как неразделительное «или»
Слайд 7
Отрицание (инверсия)
- P, P
- «не P»,
«неверно, что P»
Импликация (логическое следование)
- P→Q, P⊂Q
- «если P,
то Q», «P влечет Q», «из P следует Q»
- P-посылка импликации, Q-заключение
Эквивалентность (равнозначность)
- P∼Q, P≡Q, P↔Q
- «P эквивалентно Q», «P, если и только если Q»
Слайд 8
Неравнозначность (исключающее «ИЛИ»)
- P⊕Q, P∆Q
- «либо P, либо
Q», «или P, или Q»
- понимаются в разделительном смысле
Алфавит
логики высказываний – буквы, обозначающие высказывания, логические связки, скобки.
Логическая формула – выражение, составленное из обозначений высказываний, связок и скобок ,удовлетворяющие условиям:
любая переменная, обозначающая высказывание, - формула;
если A и B – формулы, то (A∧B), (A∨B), A, A→B, A↔B, A⊕B – формулы;
других формул нет.
Слайд 9
Пример 1.
Представить логическими формулами следующие высказывания:
Сегодня понедельник или
вторник.
Идёт дождь или снег.
Если идёт дождь, то крыши мокрые.
Дождя нет, а крыши мокрые.
Что в лоб, что по лбу.
A⊕B
A∨B
(A→B)&(A&B)
A∼B
Слайд 10
Пример 2.
Записать логическими формулами следующие высказывания:
Если допоздна работаешь
с компьютером и при этом пьёшь много кофе, то
утром просыпаешься в дурном расположении духа или с головной болью.
Если исследования показывают, что потребитель отдаёт предпочтение удобству и многообразию выбора, то фирме следует сделать упор на усовершенствование товара или увеличение многообразия новых форм.
(X&Y)→(A∨B).
42=16 различных логических интерпретаций.