характеристикам, идут навстречу друг другу. Нас интересует возникающее колебательное
движение среды, в которой распространяются волны.Различие в направлении распределения учитывается различием в знаках координаты в уравнении волны.
Наложение двух волн, бегущих в противоположные стороны
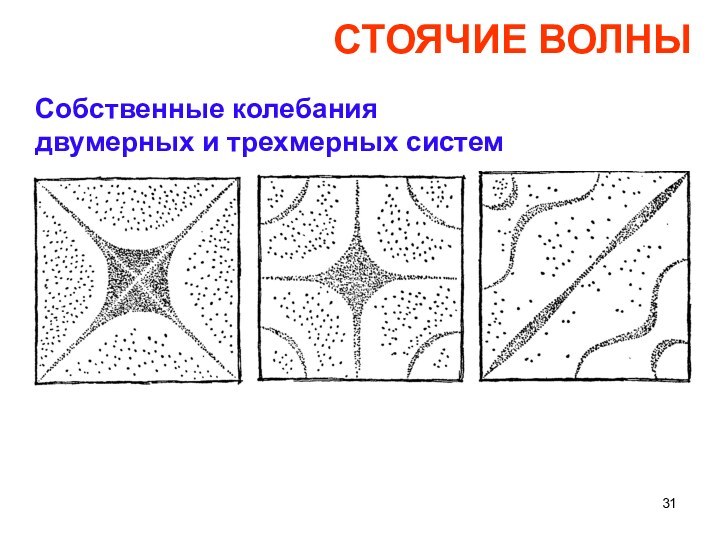
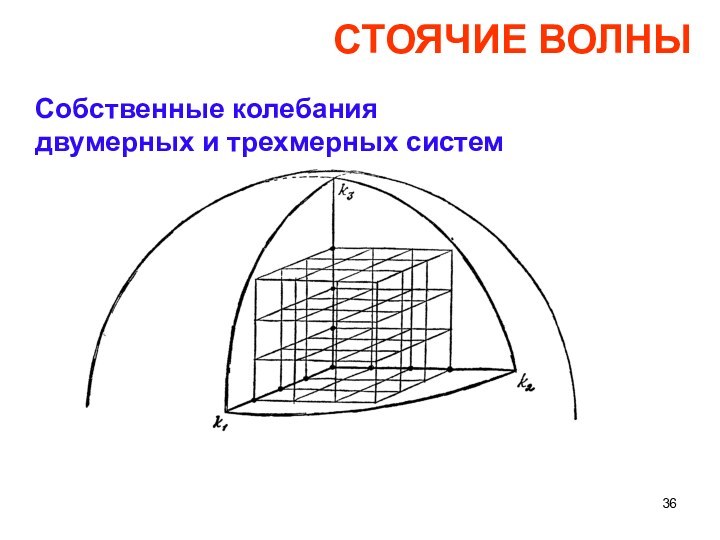
СТОЯЧИЕ ВОЛНЫ