Слайд 2
Учебные вопросы:
1. Масштаб карты.
2. Измерение по карте расстояний.
3.Определение
по карте прямоугольных и географических координат точек. Нанесение точек
на карту по известным координатам.
4. Углы положения, их взаимосвязь и измерение. Понятие тысячной. Поправка направления.
Слайд 3
Бызов Б.Е. «Военная топография». М.: Воениздат, 1980г.
Псарев А.А.
«Военная топография». М.: Воениздат, 1986г.
Бубнов И.А. «Военная топография». М.:
Воениздат, 1976г.
Маслак Ю.Г. «Военная топография». М.: Академический проект; Екатеринбург: Деловая книга, 2005г.
Николаев А.С. «Военная топография». М.: Воениздат, 1997г.
Говорухин А.М. «Справочник по военной топографии». М.: 1980г.
Бесчасный В.И. «Учебное пособие по военной топографии». Псков, 1997г.
Литература:
Слайд 4
1. Масштаб карты.
Масштаб карты - одна из важнейших
ее характеристик. Он определяет степень уменьшения линий на карте
относительно горизонтальных проложений соответствующих им линий на местности.
Масштаб указан на каждом листе карты под южной (нижней) стороной рамки в числовом (численный масштаб) и графическом (линейный масштаб) виде:
Слайд 5
Численный масштаб в общем, виде, т.е. безотносительно к
какой-либо определенной системе линейных мер, обозначается на картах в
виде отношения 1:М, где М - число, указывающее, во сколько раз уменьшены длины линий на местности при изображении их на карте. Так, масштаб 1:50 000 означает, что любой единице длины на карте соответствует 50 000 таких же единиц на местности.
Для практического использования при измерениях по карте численный масштаб, кроме того, представляют именованным числом, указывая непосредственно величину масштаба, т.е. расстояние на местности, соответствующее 1 см карты. Так, 1:50 000 карты величина масштаба равна 500 метров.
Слайд 6
Линейный масштаб представляет собой график, предназначенный для непосредственного
отсчета по нему расстояний (км, м), измеряемых или откладываемых
на карте. Однако в полевых условиях, когда работать приходится на сложенной карте, им пользуются сравнительно редко, а отрезки на карте измеряют с помощью миллиметровой линейки (масштабной).
Слайд 7
2. Измерение по карте расстояний.
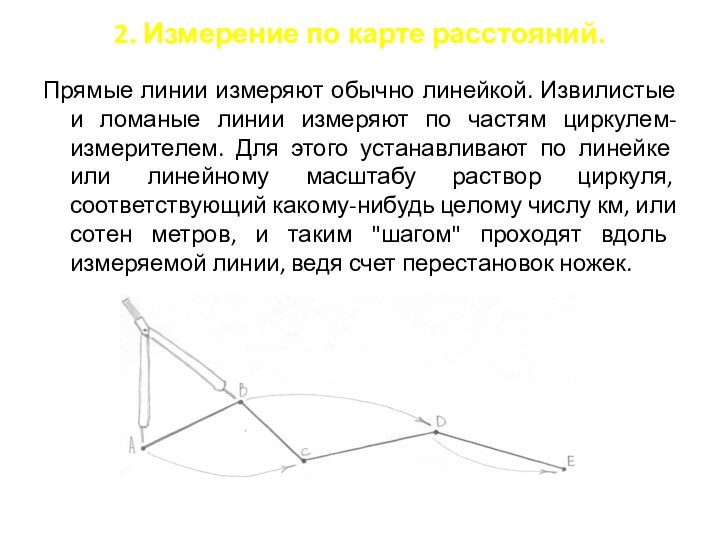
Прямые линии измеряют обычно
линейкой. Извилистые и ломаные линии измеряют по частям циркулем-измерителем.
Для этого устанавливают по линейке или линейному масштабу раствор циркуля, соответствующий какому-нибудь целому числу км, или сотен метров, и таким "шагом" проходят вдоль измеряемой линии, ведя счет перестановок ножек.
Слайд 8
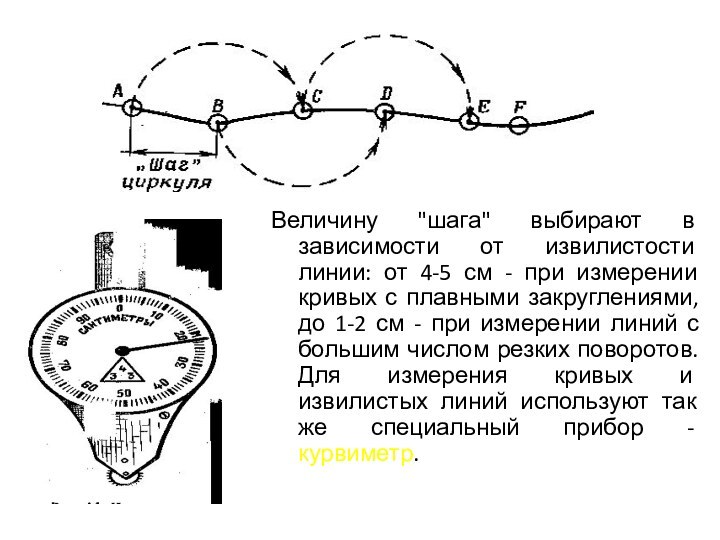
Величину "шага" выбирают в зависимости от извилистости линии:
от 4-5 см - при измерении кривых с плавными
закруглениями, до 1-2 см - при измерении линий с большим числом резких поворотов. Для измерения кривых и извилистых линий используют так же специальный прибор - курвиметр.
Слайд 9
Точность измерения расстояний по карте.
Опытным путем установлено, что
с помощью циркуля измерение прямолинейных отрезков на карте и
других чертежах не могут быть выполнены точнее, чем 0,2 мм. Расстояние на местности, соответствующее 0,2 мм на карте, называют предельной точностью масштаба карты.
Однако точность определения расстояний по карте зависит не только от точности измерений, но и от погрешностей самой карты, неизбежных при ее составлении и печатании, которые могут достигать 0,5 мм, а на картах горных районов - 0,75 мм.
Источниками ошибок измерений являются также помятость и деформация бумаги. С учетом этого фактическая точность измерения прямых линий по карте, как показывает практика, колеблется в пределах 0,5 - 1,0 мм,
что в масштабе 1:25 000 на местности составляет 12 - 25 м,
а в масштабе 1:50 000 - 25-50 м,1:100 000 - 50- 100 м.
Слайд 10
Поправки расстояний на наклон и извилистость линий.
Измеренное по

карте расстояние всегда несколько короче действительного. Одна из причин
этого состоит в том, что по карте измеряются горизонтальные проложения, В то время как соответствующие им линии на местности наклонные, т.е. длиннее своих горизонтальных проложений.
При точных расчетах, например при подготовке данных для стрельбы артиллерии в горной местности, это обстоятельство приходится учитывать и вводить соответствующие поправки.
(Поправочные коэф. для такого перехода приведены в таблице измер.в град)
Длина маршрута, измеренного по карте, бывает короче действительного не только вследствие влияния рассмотренной выше причины, но и потому, что в масштабе карты не всегда возможно изобразить все извилины дорог. При составлении карт дороги, как правило, спрямляются, и тем больше, чем мельче масштаб карты. Это особенно заметно на картах горной и холмистой местности.
Существуют таблицы в которых приведены поправочные коэффициенты в длины маршрутов, измеренных по карте. Они установлены опытным путем и учитывают как наклон, так и извилистость дорог.
(Например: горная, холмистая либо равнинная местность(данные от характера местности)
Слайд 11
Слабопересеченная местность имеет незначительное количество естественных и искусственных
препятствий, легко преодолеваема боевой и другой техникой в любом
направлении. На такой местности естественные препятствия занимают менее 10% площади. Рельеф обычно равнинный, реже холмистый.
Среднепересеченная местность имеет около 20% площади, занятой естественными препятствиями. Это наиболее распространенная разновидность хорошо обжитой местности.
Сильнопересеченная местность отличается большим количеством труднопроходимых естественных препятствий – гор с крутыми склонами, оврагов, промоин, рек, каналов и канав, болот и т.п. Площадь под естественными препятствиями составляет более 30%. Для такой местности характерны горные районы, территории с овражно-балочным и долинно-балочным рельефом.
Слайд 12
3. Определение по карте прямоугольных и географических координат
точек.
Нанесение точек на карту по их координатам.
Системы координат,
применяемые в топографии.
Координатами называются угловые и линейные величины (числа), определяющие положение точки на какой-либо поверхности или в пространстве.
В топографии применяются различные системы координат, к их числу относятся
географические,
плоские прямоугольные,
полярные
биполярные координаты.
Слайд 13
3. Определение по карте географических координат точек.
Нанесение
точек на карту по их координатам.
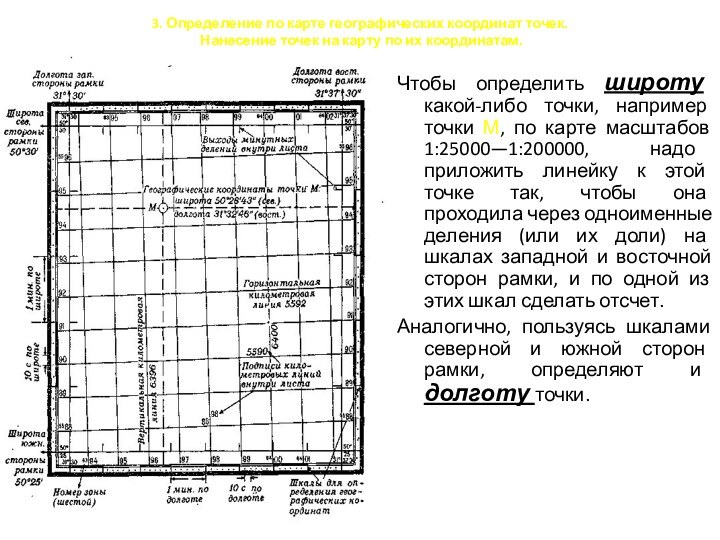
Чтобы определить широту какой-либо
точки, например точки М, по карте масштабов 1:25000—1:200000, надо приложить линейку к этой точке так, чтобы она проходила через одноименные деления (или их доли) на шкалах западной и восточной сторон рамки, и по одной из этих шкал сделать отсчет.
Аналогично, пользуясь шкалами северной и южной сторон рамки, определяют и долготу точки.
Слайд 14
На всех листах карт, (кроме карты 1:1000 000)
имеется сетка квадратов, которую называют прямоугольной координатной сеткой.
Линии сетки
проведены параллельно осям координат через 2 см на картах масштабов 1:50 000 - 1:500 000 и через 4 см на карте масштаба 1:25 000, что соответствует целому числу км. на местности. Поэтому прямоугольную координатную сетку называют так же километровой.
Километровая сетка используется для определения прямоугольных координат точек, отыскания на карте местоположения различных объектов при докладах, постановке задач, составлении донесений, для быстрой глазомерной оценки расстояний и ориентирования карты.
Километровые линии, ближайшие к углам рамки листа карты, подписывают полным числом км, остальные - сокращенно, последними двумя цифрами.
Прямоугольная координатная сетка на топографических картах.
Слайд 15
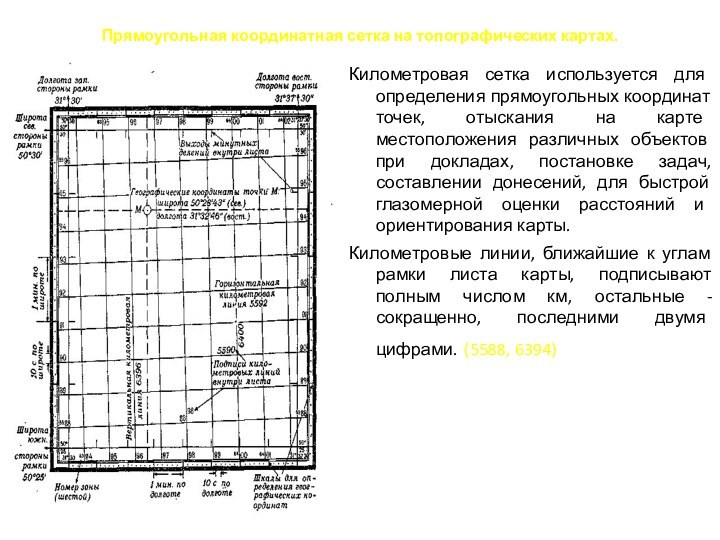
Прямоугольная координатная сетка на топографических картах.
Километровая сетка используется
для определения прямоугольных координат точек, отыскания на карте местоположения
различных объектов при докладах, постановке задач, составлении донесений, для быстрой глазомерной оценки расстояний и ориентирования карты.
Километровые линии, ближайшие к углам рамки листа карты, подписывают полным числом км, остальные - сокращенно, последними двумя цифрами. (5588, 6394)
Слайд 16
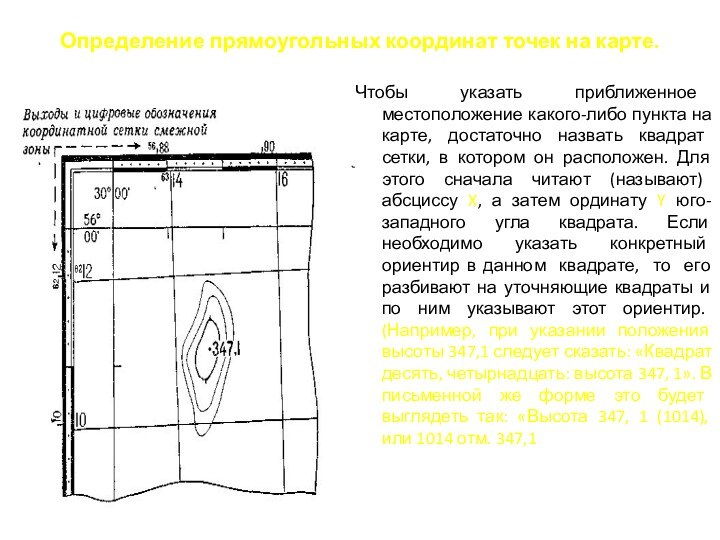
Определение прямоугольных координат точек на карте.
Чтобы указать приближенное
местоположение какого-либо пункта на карте, достаточно назвать квадрат сетки,
в котором он расположен. Для этого сначала читают (называют) абсциссу X, а затем ординату Y юго-западного угла квадрата. Если необходимо указать конкретный ориентир в данном квадрате, то его разбивают на уточняющие квадраты и по ним указывают этот ориентир. (Например, при указании положения высоты 347,1 следует сказать: «Квадрат десять, четырнадцать: высота 347, 1». В письменной же форме это будет выглядеть так: «Высота 347, 1 (1014), или 1014 отм. 347,1
Слайд 17
Определение прямоугольных координат точек на карте.
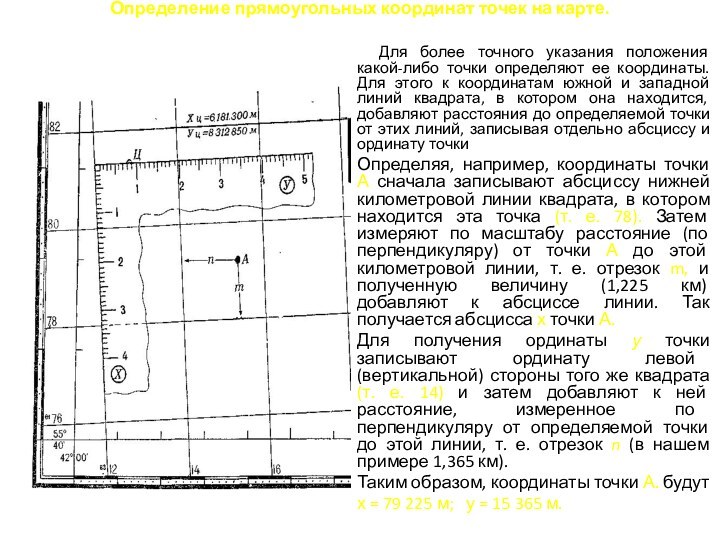
Для более точного
указания положения какой-либо точки определяют ее координаты. Для этого
к координатам южной и западной линий квадрата, в котором она находится, добавляют расстояния до определяемой точки от этих линий, записывая отдельно абсциссу и ординату точки
Определяя, например, координаты точки А сначала записывают абсциссу нижней километровой линии квадрата, в котором находится эта точка (т. е. 78). Затем измеряют по масштабу расстояние (по перпендикуляру) от точки А до этой километровой линии, т. е. отрезок m, и полученную величину (1,225 км) добавляют к абсциссе линии. Так получается абсцисса х точки А.
Для получения ординаты у точки записывают ординату левой (вертикальной) стороны того же квадрата (т. е. 14) и затем добавляют к ней расстояние, измеренное по перпендикуляру от определяемой точки до этой линии, т. е. отрезок n (в нашем примере 1,365 км).
Таким образом, координаты точки А. будут
х = 79 225 м; у = 15 365 м.
Слайд 18
Определение прямоугольных координат точек на карте.
Так как в
данном случае при определении координат точки цифровое обозначение километровых
линий было записано не полностью а, лишь последними двумя цифрами (78 и 14), то такие координаты называют сокращенными координатами точки А.
Если же оцифровку километровых линий записывать полностью, то получим полные координаты для точки А т.е дописываем число полных километров подписанные в ближайших к углам рамки листа карты
х = 6 179225 м; у = 8315365 м.
Слайд 19
4. Углы положения, их взаимосвязь и измерение. Понятие
тысячной.
Поправка направления.
Азимуты и дирекционные углы.
В качестве начального направления
обычно принимают:
-направление, параллельное вертикальной километровой линии карты;
-направление географического меридиана, называемого также истинным меридианом;
-направление магнитной стрелки компаса, т.е. направление магнитного меридиана.
В зависимости от того, какое направление принято за начальное, различают три вида углов, определяющих направления на точки:
дирекционный угол а,
истинный азимут А
магнитный азимут Аm.
Слайд 20
Углы положения, их взаимосвязь и измерение. Понятие тысячной.
Поправка направления.
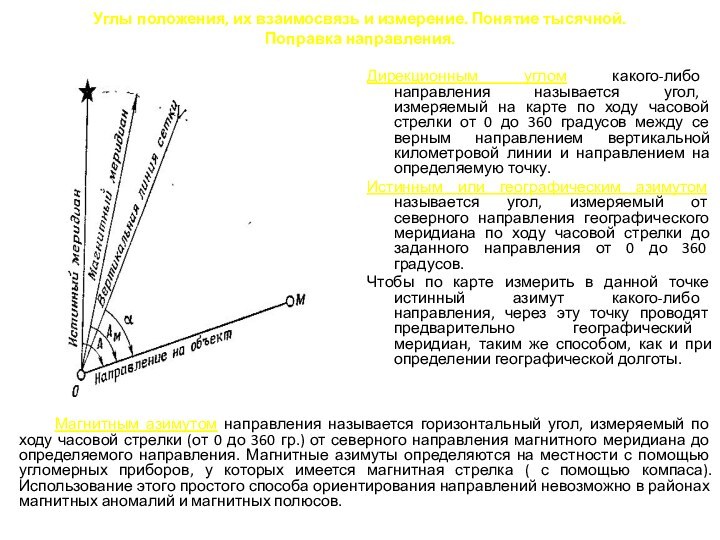
Дирекционным углом какого-либо направления называется угол, измеряемый на
карте по ходу часовой стрелки от 0 до 360 градусов между северным направлением вертикальной километровой линии и направлением на определяемую точку.
Истинным или географическим азимутом называется угол, измеряемый от северного направления географического меридиана по ходу часовой стрелки до заданного направления от 0 до 360 градусов.
Чтобы по карте измерить в данной точке истинный азимут какого-либо направления, через эту точку проводят предварительно географический меридиан, таким же способом, как и при определении географической долготы.
Магнитным азимутом направления называется горизонтальный угол, измеряемый по ходу часовой стрелки (от 0 до 360 гр.) от северного направления магнитного меридиана до определяемого направления. Магнитные азимуты определяются на местности с помощью угломерных приборов, у которых имеется магнитная стрелка ( с помощью компаса).Использование этого простого способа ориентирования направлений невозможно в районах магнитных аномалий и магнитных полюсов.
Слайд 21
Измерение и построение дирекционных углов на карте.
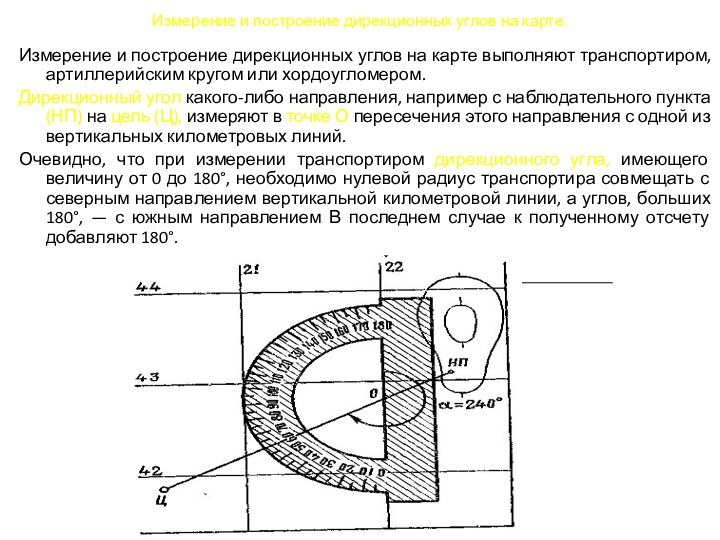
Измерение
и построение дирекционных углов на карте выполняют транспортиром, артиллерийским
кругом или хордоугломером.
Дирекционный угол какого-либо направления, например с наблюдательного пункта (НП) на цель (Ц), измеряют в точке О пересечения этого направления с одной из вертикальных километровых линий.
Очевидно, что при измерении транспортиром дирекционного угла, имеющего величину от 0 до 180°, необходимо нулевой радиус транспортира совмещать с северным направлением вертикальной километровой линии, а углов, больших 180°, — с южным направлением В последнем случае к полученному отсчету добавляют 180°.
Слайд 22
Понятие тысячной.
Шкалы транспортиров построены чаще всего в градусной
мере, артиллерийских кругов и хордоугломеров — в делениях угломера.
В делениях угломера окружность разделена на 60 больших или 6000 малых делений Одно малое деление угломера называют также тысячной. Такое название объясняется тем, что длина отрезка дуги окружности, соответствующего одному малому делению, равна округленно тысячной доле радиуса этой окружности, так как
В этом и заключается преимущество данной меры углов по сравнению с градусной: единицей измерения угла здесь служит линейный отрезок, равный тысячной доле дистанции. Это позволяет быстро и легко посредством простейших арифметических действий переходить от угловых измерений к линейным и обратно.
Слайд 23
Понятие тысячной.
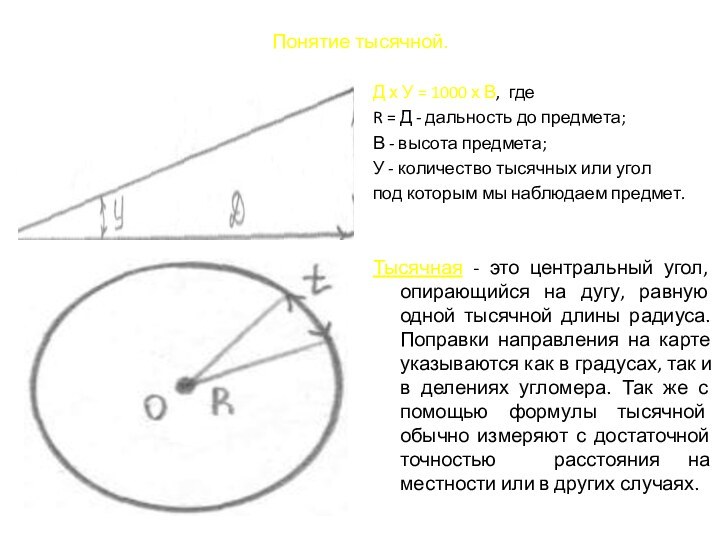
Д х У = 1000 х В,
где
R = Д - дальность до предмета;
В - высота
предмета;
У - количество тысячных или угол
под которым мы наблюдаем предмет.
Тысячная - это центральный угол, опирающийся на дугу, равную одной тысячной длины радиуса. Поправки направления на карте указываются как в градусах, так и в делениях угломера. Так же с помощью формулы тысячной обычно измеряют с достаточной точностью расстояния на местности или в других случаях.
Слайд 24
Понятие тысячной.
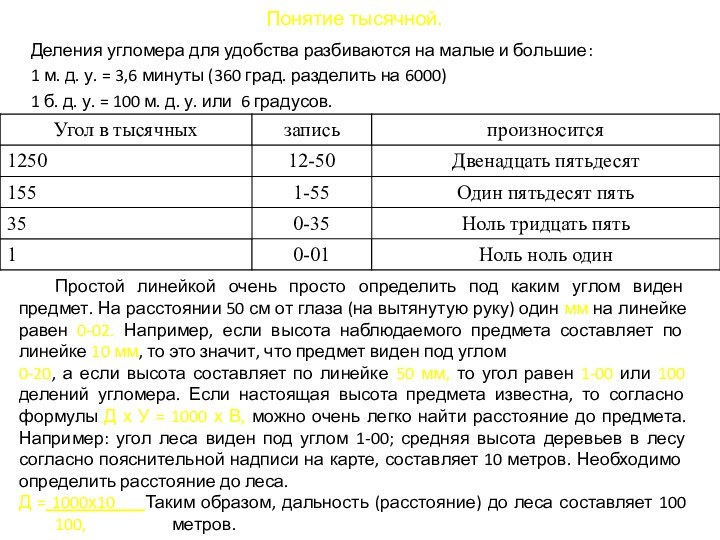
Деления угломера для удобства разбиваются на малые
и большие:
1 м. д. у. = 3,6 минуты (360
град. разделить на 6000)
1 б. д. у. = 100 м. д. у. или 6 градусов.
Простой линейкой очень просто определить под каким углом виден предмет. На расстоянии 50 см от глаза (на вытянутую руку) один мм на линейке равен 0-02. Например, если высота наблюдаемого предмета составляет по линейке 10 мм, то это значит, что предмет виден под углом
0-20, а если высота составляет по линейке 50 мм, то угол равен 1-00 или 100 делений угломера. Если настоящая высота предмета известна, то согласно формулы Д х У = 1000 х В, можно очень легко найти расстояние до предмета. Например: угол леса виден под углом 1-00; средняя высота деревьев в лесу согласно пояснительной надписи на карте, составляет 10 метров. Необходимо определить расстояние до леса.
Д = 1000х10 Таким образом, дальность (расстояние) до леса составляет 100 100, метров.
Слайд 25
Переход от дирекционного угла к магнитному азимуту и
обратно. Поправка направления.
Переход от дирекционного угла к магнитному азимуту
и обратно выполняют тогда, когда на местности необходимо с помощью компаса найти направление, дирекционный угол которого измерен по карте, или наоборот, когда на карту необходимо нанести направление, магнитный азимут которого измерен на местности с помощью компаса.
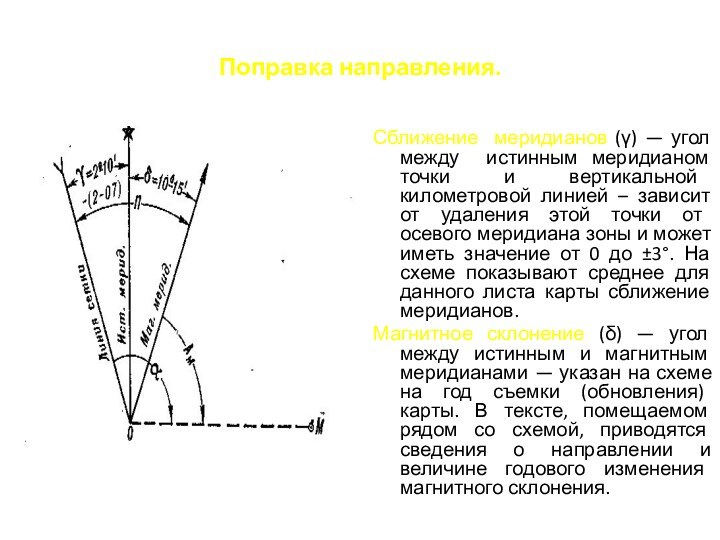
Для решения этой задачи необходимо знать величину отклонения магнитного меридиана данной точки от вертикальной километровой линии. Эту величину называют поправкой направления.
Поправка направления и составляющие ее углы - сближение меридианов и магнитное склонение - указывают на карте под южной стороной рамки в виде схемы