1 февраля 2011 года банк заданий содержал 82 прототипа
заданий В12.Среди них задач на проценты
16 прототипов.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Текстовые задачи на проценты в заданиях ЕГЭ по математике
Содержание
- 2. Открытый банк заданий ЕГЭ по математике
- 7. В ситуациях образования одних сплавов из
- 8. Полезные формулыА – вещество в сплавеМ –
- 9. Способ 15*0,12=0,6(л.)-вещества содержится в 5 литрах 12%
- 10. 2Хл.Хл.Хл.+=15%19% y%15Х+19Х=2ХYY=17Ответ: 17% - концентрация получившегося
- 11. № 99572 Смешали некоторое количество 15-процентного раствора
- 12. 10л.6л.4Л.+= 15% 25% Х%15*4+6*25=10Х60+150=10ХХ=21 Ответ: 21%
- 13. Х кг(200-Х) кг200кг+=10%30%25%1. 10Х + 30(200-Х) =
- 14. Х кг(3+Х)кг(2Х+3)кг+= 10% 40% 30%1. 10Х
- 15. (Х+у+10)кгУ кгХ кг+ =30% 60%
- 16. {30Х + 60 У = 36(Х+У+10)30Х +
- 17. 50кг20кг30кг+=Х%У%68%2ZкгZкг+= Х% У%70%Zкг№ 99578 Имеются два сосуда.
- 18. {30Х + 20 У = 50*68ZX +
- 19. Закон сохранения массы сухого веществаВ задачах о
- 20. Виноград Х кгВлажность 90%Сухое вещество 10%Изюм 20 кгВлажность 5%Сухое вещество 95%20кг. –
- 21. 400000 * 1,08 = 43200 чел.
- 22. 1. Хр. – 100% Ур. –
- 23. 1. Ур. – 100% 4Хр. –
- 24. Увеличение прибыли на 300% означает, что Бубликов
- 25. № 99568Семья состоит из мужа, жены и
- 26. 1) Пусть новая стоимость холодильника через год
- 27. В презентации использованы материалы: Текстовые задачи из открытого банка заданий ЕГЭ по математике http://www.mathege.ru
- 28. Скачать презентацию
- 29. Похожие презентации
Открытый банк заданий ЕГЭ по математике На 1 февраля 2011 года банк заданий содержал 82 прототипа заданий В12. Среди них задач на проценты 16 прототипов.
Слайд 7 В ситуациях образования одних сплавов из других
обычно (если другое не оговорено в условии задачи) принимается
закон сохранения массы: общая масса сплава равна сумме масс составляющих его частей (сплавов) и общая масса каждого вещества в сплаве равна сумме масс этого вещества во всех составляющих частях. В промышленности часто используют не чистые металлы, а их смеси – сплавы. В сплаве свойства разных компонентов удачно взаимно дополняются.
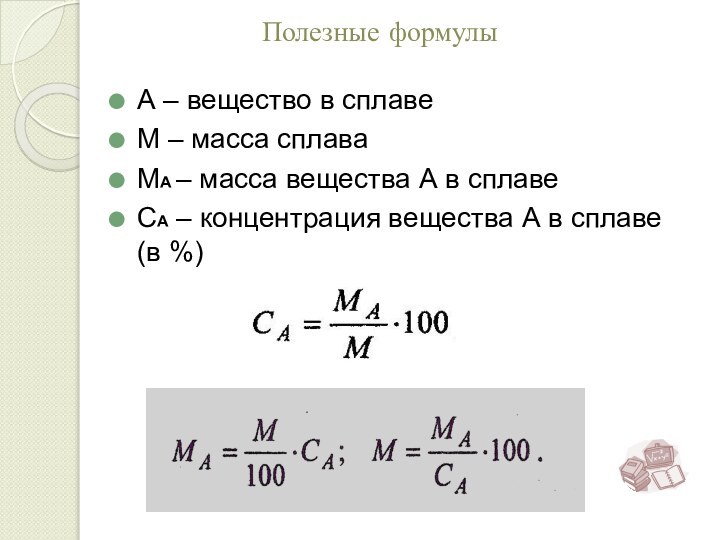
Раствор – это гомогенная система, состоящая из 2х или более веществ, содержание которых можно изменить в определенных пределах без нарушения однородности.
Состав растворов обычно передается содержанием в них растворенного вещества в виде массовой доли или концентрации.
Основные понятия в задачах на смеси, сплавы, растворы
Слайд 8
Полезные формулы
А – вещество в сплаве
М – масса
сплава
МА – масса вещества А в сплаве
СА – концентрация
вещества А в сплаве (в %)
Слайд 9
Способ 1
5*0,12=0,6(л.)-вещества содержится в 5 литрах 12% раствора
5+7=12(л.)
– объем получившегося раствора
12л.--- 100%
0,6л. --- X%
Х=5%
Ответ: 5% -
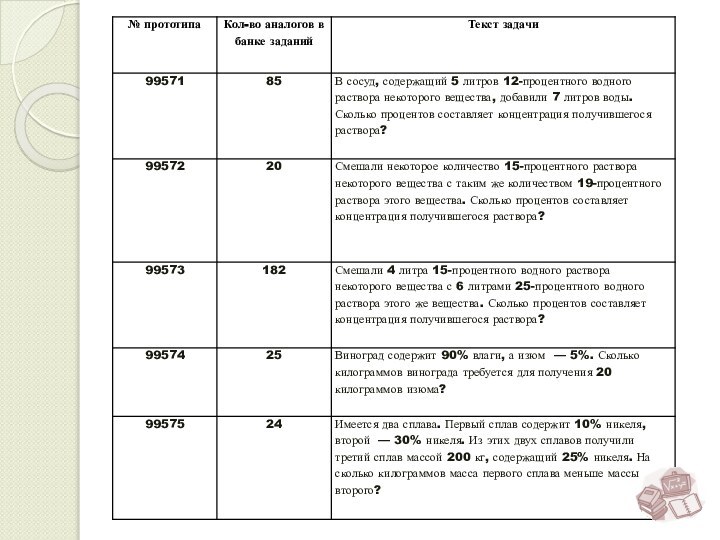
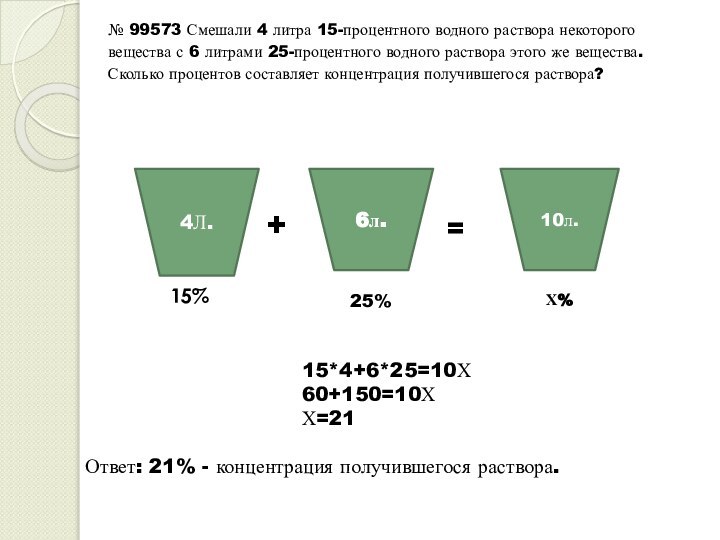
концентрация получившегося раствора.№ 99571 В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Слайд 10
2Хл.
Хл.
Хл.
+
=
15%
19%
y%
15Х+19Х=2ХY
Y=17
Ответ: 17% - концентрация получившегося раствора.
№
99572 Смешали некоторое количество 15-процентного раствора некоторого вещества с
таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?Слайд 11 № 99572 Смешали некоторое количество 15-процентного раствора некоторого
вещества с таким же количеством 19-процентного раствора этого вещества.
Сколько процентов составляет концентрация получившегося раствора?Если массы исходных растворов равны, то концентрация их смеси равна среднему арифметическому концентраций смешиваемых жидкостей.
Ответ : 17% концентрация получившегося
раствора
(15+19) : 2 = 17
Слайд 12
10л.
6л.
4Л.
+
=
15%
25%
Х%
15*4+6*25=10Х
60+150=10Х
Х=21
Ответ: 21% -
концентрация получившегося раствора.
№ 99573 Смешали 4 литра 15-процентного водного
раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Слайд 13
Х кг
(200-Х) кг
200кг
+
=
10%
30%
25%
1. 10Х + 30(200-Х) = 200*25
10Х + 6000 - 30Х = 5000
Х=50(кг) –масса первого сплава.2. 200 – 50 = 150 (кг) – масса второго сплава
3. 150 – 50 = 100 (кг)
Ответ: на 100 кг масса первого сплава
меньше массы второго сплава.
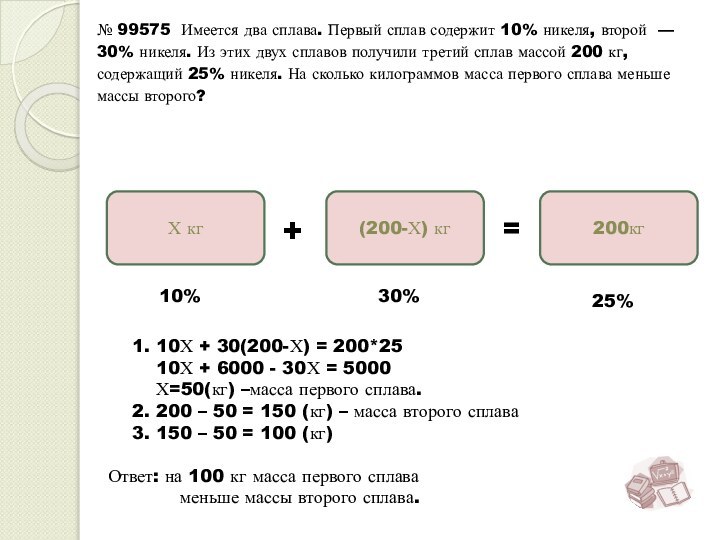
№ 99575 Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Слайд 14
Х кг
(3+Х)кг
(2Х+3)кг
+
=
10%
40%
30%
1. 10Х +
40(3 + Х) = 30(2Х+3)
10Х + 120
+ 40Х = 60Х + 90Х=3(кг) –масса первого сплава.
2. 2*3+3=9(кг)
Ответ: 9 кг масса третьего сплава.
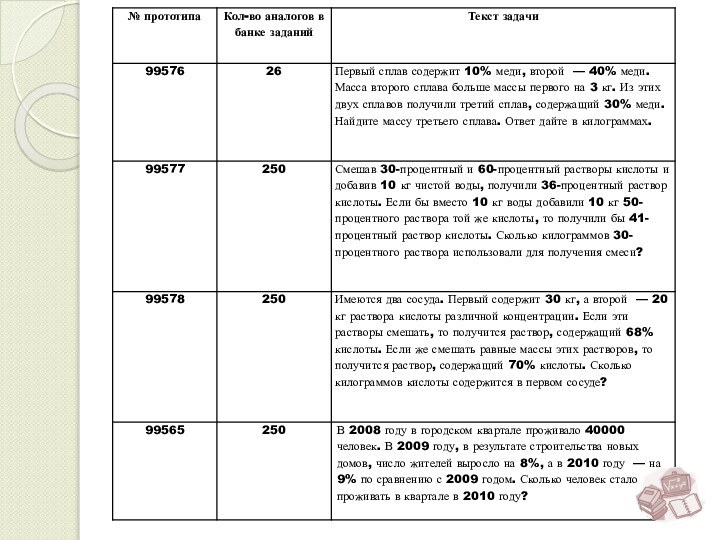
№ 99576 Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Слайд 15
(Х+у+10)кг
У кг
Х кг
+
=
30%
60%
36%
+
10кг
0%
(Х+у+10)кг
У кг
Х кг
+
=
30%
60%
41%
+
10кг
50%
№ 99577
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Слайд 16
{
30Х + 60 У = 36(Х+У+10)
30Х + 60
У + 500 = 41(Х+У+10)
-6Х + 24У = 360
-11Х
+ 19У = -90{
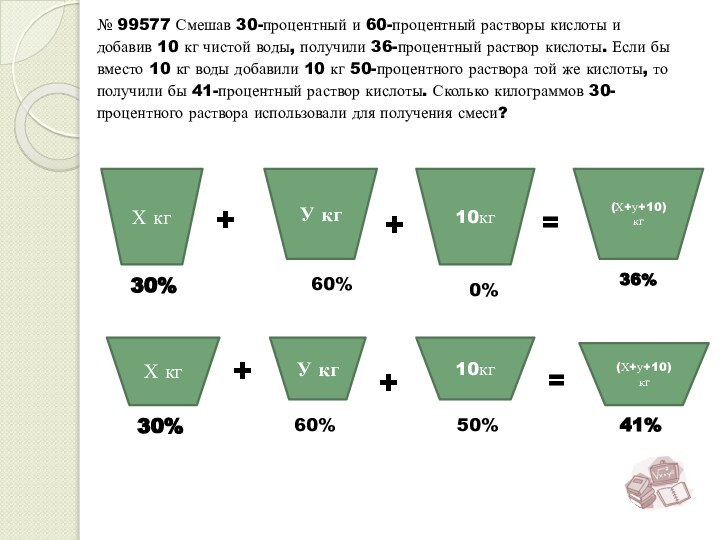
Х- 4У = -60
-11Х + 19У = -90
{
11Х – 44У = -660
-11Х + 19У = -90
{
Х = 60
Ответ: для получения смеси использовали 60 кг
30 – процентного раствора
Слайд 17
50кг
20кг
30кг
+
=
Х%
У%
68%
2Zкг
Zкг
+
=
Х%
У%
70%
Zкг
№ 99578 Имеются два сосуда. Первый
содержит 30 кг, а второй — 20 кг раствора
кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Слайд 18
{
30Х + 20 У = 50*68
ZX + ZУ
= 140Z
{
3Х + 2 У = 340
X + У
= 140{
3Х + 2 У = 340
-2X - 2У = -280
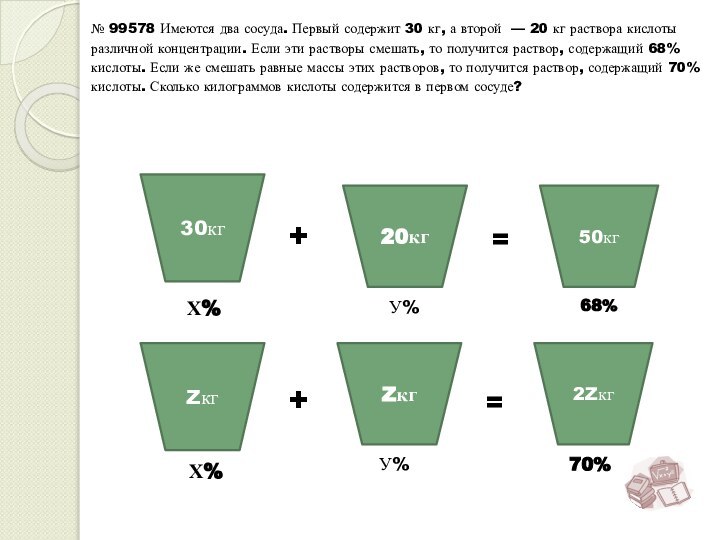
X=60% - процентная концентрация первого раствора
30*60/100 = 18 (кг)
Ответ : в первом растворе содержится 18 кг кислоты
Слайд 19
Закон сохранения массы сухого вещества
В задачах о просушивании
зерна, травы в процессе ее превращения в сено, винограда
в процессе его превращения в изюм и др. просушиваемый продукт представляется состоящим из воды и сухого вещества.Концентрацию воды в этом продукте называют влажностью.
Ключевым моментом решения подобной задачи является использование закона сохранения массы сухого вещества в процессе просушивания рассматриваемого продукта.
В процессе просушивания продукта влажность изменяется, а сухое вещество остается прежним.
Слайд 20
Виноград Х кг
Влажность 90%
Сухое вещество 10%
Изюм 20 кг
Влажность 5%
Сухое вещество 95%
20кг. – 100%:
У
кг . - 95%
У= 19 кг – сухого
вещества содержится в 20 кг. изюма2. Xкг. – 100%
19кг. – 10%
Х=190 кг
Ответ : для получения 20 кг. изюма требуется 190 кг винограда
№99574 Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Слайд 21 400000 * 1,08 = 43200 чел. –
проживало
в городском квартале в 2009 году
2.
43200 * 1,09 = 47088 чел.Ответ : в городском квартале в 2010 году проживало 47088 человек
№ 99565 В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году — на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
Слайд 22
1. Хр. – 100%
Ур. – (100
+ t)%
У = 0,01Х * (100 +t)
– рублей стоят акции в понедельник
2. 0,01Х * (100 +t)р. – 100%
Zр. - (100-t)%
Z = 0,0001Х *(10000- t2)р. – стоят акции во вторник
3. Хр. – 100%
0,0001Х *(10000- t2)р. – 96%
96 Х = 0,01Х * (10000- t2)
9600 = 10000 - t2
t = 20
Ответ : акции подорожали в понедельник на 20%
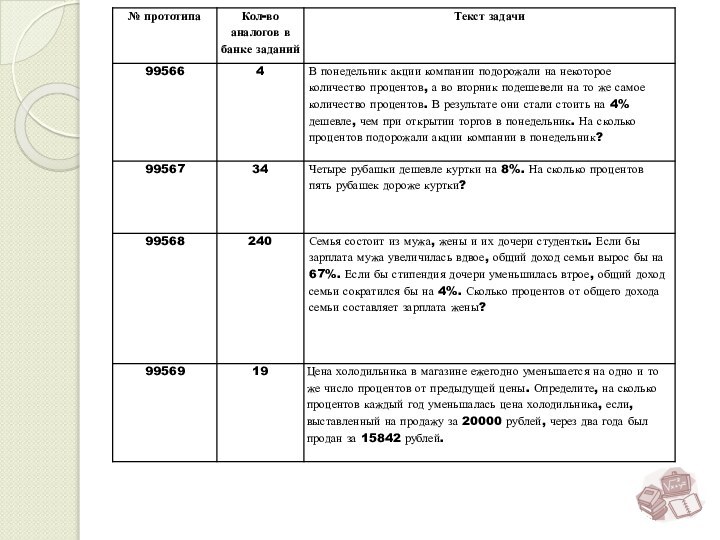
№ 99566 В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Слайд 23
1. Ур. – 100%
4Хр. – 92%
4Х = 0,92У
Х = 0,23У р.
– стоит одна рубашка2. 0,23У *5 = 1,15 Ур. – стоят 5 рубашек
3. Ур. – 100 %
1,15Ур. – t%
t = 115 % - составляет 5 курток
4. 115 – 100= 15%
Ответ : на 15% 5 рубашек дороже куртки.
№99567 Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?
Слайд 24 Увеличение прибыли на 300% означает, что Бубликов заработал
400% от прибыли прошлого года.
Ответ: в 2003 году прибыли
составила 320000 руб.№ 99586
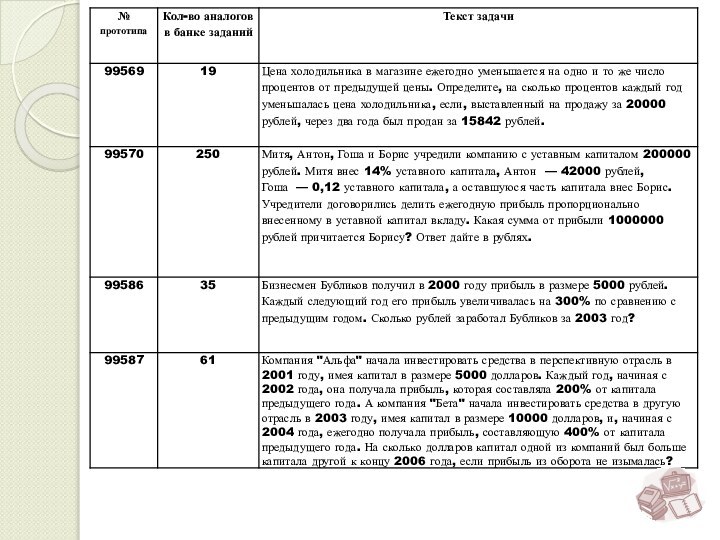
Бизнесмен Бубликов получил в 2000 году прибыль в размере 5000 рублей. Каждый следующий год его прибыль увеличивалась на 300% по сравнению с предыдущим годом. Сколько рублей заработал Бубликов за 2003 год?
Слайд 25
№ 99568
Семья состоит из мужа, жены и их
дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий
доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?Пусть х - общий доход семьи
Рассмотрим уравнения (М-доход мужа, Ж-доход жены, Д- доход дочери)
1. М + Ж + Д = х
2. 2М + Ж + Д = 1,67х
3. М + Ж + Д/3 = 0,96х
Из 2-го уравнения вычитаем 1-е уравнение
М = 0,67х
Из 1-го уравнения вычитаем 3-е уравнение
2Д/3 = 0,04х
Д = 0,06х
Отсюда
Ж = х - М - Д = х - 0,67х - 0,06х = 0,27х
Ответ: 27%
Слайд 26 1) Пусть новая стоимость холодильника через год составляет
х % от первоначальной стоимости. Тогда можно составить уравнение:
20000*0,01Х*0,01Х=15842
Х=89
2)100-89=11%
Ответ:
цена холодильника ежегодно уменьшалась на 11% № 99569 Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рублей.
Слайд 27
В презентации использованы материалы:
Текстовые задачи из открытого
