Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Тема 12. САМОИНДУКЦИЯ И ВЗАИМНАЯ ИНДУКЦИЯ.

Содержание

2. 12.1. Явление самоиндукцииДо сих пор мы рассматривали
3. Здесь возможны два случая: при изменении тока
4. ЭДС индукции, возникающая в
5. Джозеф. Генри
6. Явление самоиндукции: Ток I, текущий в любом
7. Т.к. магнитная индукция В пропорциональна току
8. За единицу индуктивности в СИ
9. Вычислим индуктивность соленоида L. Если длина
10. Мы знаем, что
11. Можно найти размерность для μ0 При изменении
12. 12.2. Влияние самоиндукции на ток при размыкании
13. Это приводит к тому, что при замыкании
14. Случай 2. При переводе ключа
15. Случай 3. Размыкание цепи содержащей индуктивность L.
16. Ei резко возрастает по сравнению с
17. 12.3. Взаимная индукцияВозьмем два контура, расположенные недалеко
18. При изменении тока I1 во втором контуре
19. Контуры называются связанными, а явление – взаимной
20. а – при движении зарядов контура
21. Непрерывно меняющийся ток в катушке
22. 12.4. Индуктивность трансформатораЯвление взаимной индукции используется в
23. Рассчитаем взаимную индуктивность двух катушек L1 и
24. Через вторую обмотку проходит полный магнитный поток
25. Тогда переменная ЭДС в первичной обмотке:
26. 12.5. Энергия магнитного поляРассмотрим случай, о котором
27. (12.5.2)Эта работа пойдет
28. Выразим энергию через параметры магнитного
29. Обозначим w – плотность энергии,
30. Энергия однородного магнитного поля в длинном соленоиде
31. Скачать презентацию
32. Похожие презентации

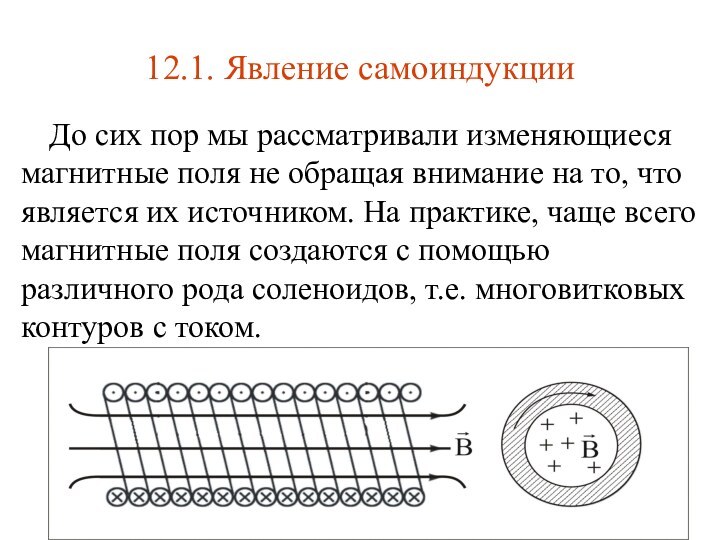
12.1. Явление самоиндукцииДо сих пор мы рассматривали изменяющиеся магнитные поля не обращая внимание на то, что является их источником. На практике, чаще всего магнитные поля создаются с помощью различного рода соленоидов, т.е. многовитковых контуров с током.

Главная
Разное
Тема 12. САМОИНДУКЦИЯ И ВЗАИМНАЯ ИНДУКЦИЯ.

Тема 12. САМОИНДУКЦИЯ И ВЗАИМНАЯ ИНДУКЦИЯ. 12.1. Явление самоиндукции.12.2. Влияние самоиндукции на

12.1. Явление самоиндукцииДо сих пор мы рассматривали изменяющиеся магнитные поля не обращая

Здесь возможны два случая: при изменении тока в контуре изменяется магнитный поток,

ЭДС индукции, возникающая в самом же контуре называется ЭДС

Явление самоиндукции: Ток I, текущий в любом контуре создает магнитный поток Ψ,

Т.к. магнитная индукция В пропорциональна току I (В = μμ0nI),

За единицу индуктивности в СИ принимается индуктивность такого контура, у

Вычислим индуктивность соленоида L. Если длина соленоида l гораздо больше его

Можно найти размерность для μ0 При изменении тока в контуре в нем

12.2. Влияние самоиндукции на ток при размыкании и замыкании цепи, содержащей индуктивностьСлучай

Это приводит к тому, что при замыкании ключа К установление тока I2

Случай 2. При переводе ключа из положения 1 в 2

Случай 3. Размыкание цепи содержащей индуктивность L. Т.к. цепь разомкнута, ток не

Ei резко возрастает по сравнению с E0 и даже может быть

12.3. Взаимная индукцияВозьмем два контура, расположенные недалеко друг от другаВ первом контуре

При изменении тока I1 во втором контуре наводится ЭДС индукции (12.3.2)Аналогично, ток I2

Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты L21 и L12

а – при движении зарядов контура 2 в магнитном поле контура

Непрерывно меняющийся ток в катушке (а) создает переменное магнитное поле,

12.4. Индуктивность трансформатораЯвление взаимной индукции используется в широко распространенных устройствах – трансформаторах.Трансформатор

Рассчитаем взаимную индуктивность двух катушек L1 и L2, намотанных на общий сердечник

Через вторую обмотку проходит полный магнитный поток Ψ2 сцепленный со второй обмоткой (12.4.2)К

Тогда переменная ЭДС в первичной обмотке: (12.4.4)Во вторичной обмотке,

12.5. Энергия магнитного поляРассмотрим случай, о котором мы уже говорили: Сначала замкнем соленоид

(12.5.2)Эта работа пойдет на нагревание проводников. Но откуда

Выразим энергию через параметры магнитного поля. Индуктивность соленоида

Обозначим w – плотность энергии, или энергия в объеме V,

Энергия однородного магнитного поля в длинном соленоиде может быть рассчитана по формуле

Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из

Слайды презентации

Слайд 2 12.1. Явление самоиндукции
До сих пор мы рассматривали изменяющиеся

12.1. Явление самоиндукцииДо сих пор мы рассматривали изменяющиеся магнитные поля не

магнитные поля не обращая внимание на то, что является

их источником. На практике, чаще всего магнитные поля создаются с помощью различного рода соленоидов, т.е. многовитковых контуров с током.

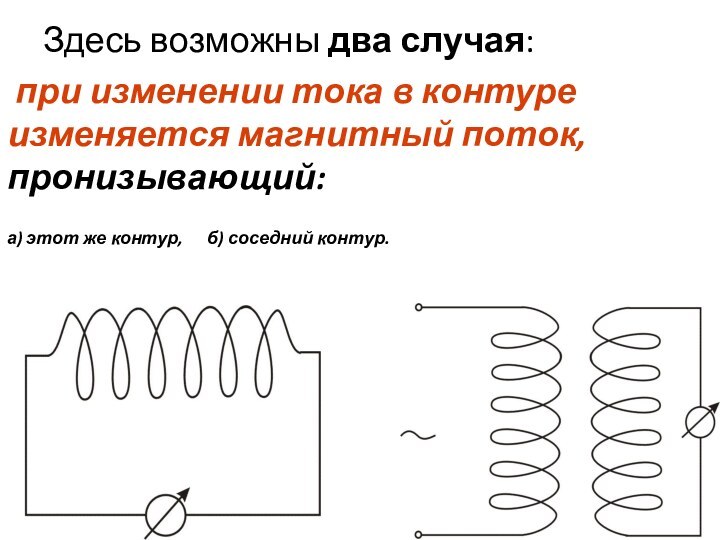
Слайд 3 Здесь возможны два случая:
при изменении тока в

Здесь возможны два случая: при изменении тока в контуре изменяется магнитный

контуре изменяется магнитный поток, пронизывающий:

а) этот же контур,

б) соседний контур.

Слайд 4 ЭДС индукции, возникающая в самом

же контуре называется ЭДС самоиндукции, а само явление –

самоиндукция.

Если же ЭДС индукции возникает в соседнем контуре, то говорят о явлении взаимной индукции.

Ясно, что природа явления одна и та же, а разные названия – чтобы подчеркнуть место возникновения ЭДС индукции.
Явление самоиндукции открыл американский ученый Дж. Генри в 1831 г.

Слайд 5 Джозеф. Генри (1797

– 1878г) президент Национальной АН

США
Работы посвящены электро- магнетизму.
Кроме принципа магнитной индукции Генри изобрел электромагнитное реле, построил электродвигатель, телеграф
на территории колледжа в Пристоне.

Слайд 6 Явление самоиндукции:

Ток I, текущий в любом контуре

Явление самоиндукции: Ток I, текущий в любом контуре создает магнитный поток

создает магнитный поток Ψ, пронизывающего этот же контур.
При

изменении I, будет изменятся Ψ , следовательно в контуре будет наводится ЭДС индукции.

Слайд 7 Т.к. магнитная индукция В пропорциональна току I

(В = μμ0nI), следовательно
Ψ = LI,
где

L – коэффициент пропорциональности, названный индуктивностью контура.

L = const, если внутри контура нет ферромагнетиков, т.к. μ = f(I) = f(H)

Индуктивность контура L зависит от геометрии контура: числа витков, площади витка контура.

Слайд 8 За единицу индуктивности в СИ принимается

индуктивность такого контура, у которого при токе I

= 1А возникает полный поток Ψ = 1Вб.
Эта единица называется Генри (Гн).
Размерность индуктивности

Слайд 9 Вычислим индуктивность соленоида L.
Если длина соленоида

Вычислим индуктивность соленоида L. Если длина соленоида l гораздо больше

l гораздо больше его диаметра d ( l >>

d), то к нему можно применить формулы для бесконечно длинного соленоида.
Тогда
(12.1.1)
Здесь N – число витков.
Поток через каждый из витков Ф = ВS
Потокосцепление
(12.1.2)

Слайд 10 Мы знаем, что

,

тогда индуктивность соленоида
(12.1.3)
где n – число витков на единицу длины, т.е.

V – объем соленоида, значит

Слайд 11 Можно найти размерность для μ0

При изменении тока

Можно найти размерность для μ0 При изменении тока в контуре в

в контуре в нем возникает ЭДС самоиндукции, равная

(12.1.5)

Знак

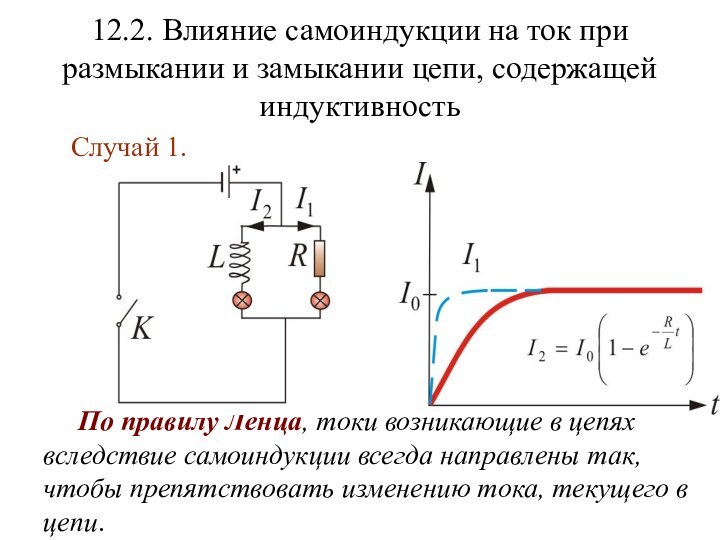
минус в этой формуле обусловлен правилом Ленца.

Слайд 12 12.2. Влияние самоиндукции на ток при размыкании и

12.2. Влияние самоиндукции на ток при размыкании и замыкании цепи, содержащей

замыкании цепи, содержащей индуктивность
Случай 1.

По правилу

Ленца, токи возникающие в цепях вследствие самоиндукции всегда направлены так, чтобы препятствовать изменению тока, текущего в цепи.

Слайд 13
Это приводит к тому, что при замыкании ключа

Это приводит к тому, что при замыкании ключа К установление тока

К установление тока I2 в цепи содержащей индуктивность L

,будет происходить не мгновенно, а постепенно.
Сила тока в этой цепи будет удовлетворять уравнению

(12.2.1)
Скорость возрастания тока будет характеризоваться постоянной времени цепи
(12.2.2)
В цепи, содержащей только активное сопротивление R ток I1 установится практически мгновенно.

Слайд 14 Случай 2.

При переводе ключа из

положения 1 в 2 в момент времени t0, ток

начнет уменьшаться но ЭДС самоиндукции будет поддерживать ток в цепи, т.е. препятствовать резкому уменьшению тока. В этом случае убывание тока в цепи можно описать уравнением

(12.2.3)
Оба эти случая говорят, что чем больше индуктивность цепи L и чем меньше сопротивление R, тем больше постоянная времени τ и тем медленнее изменяется ток в цепи.

Слайд 15 Случай 3. Размыкание цепи содержащей индуктивность L.

Т.к.

Случай 3. Размыкание цепи содержащей индуктивность L. Т.к. цепь разомкнута, ток

цепь разомкнута, ток не течёт, поэтому рисуем зависимость Ei(t)

.
При размыкании цепи в момент времени t0
Это приводит к резкому возрастанию ЭДС индукции, определяемой по формуле

Происходит этот скачок вследствие большой величины скорости изменения тока .

Слайд 16

Ei резко возрастает по сравнению с E0

и даже может быть в несколько раз больше E0.

Нельзя резко размыкать цепь, состоящую из трансформатора и других индуктивностей.

Слайд 17 12.3. Взаимная индукция
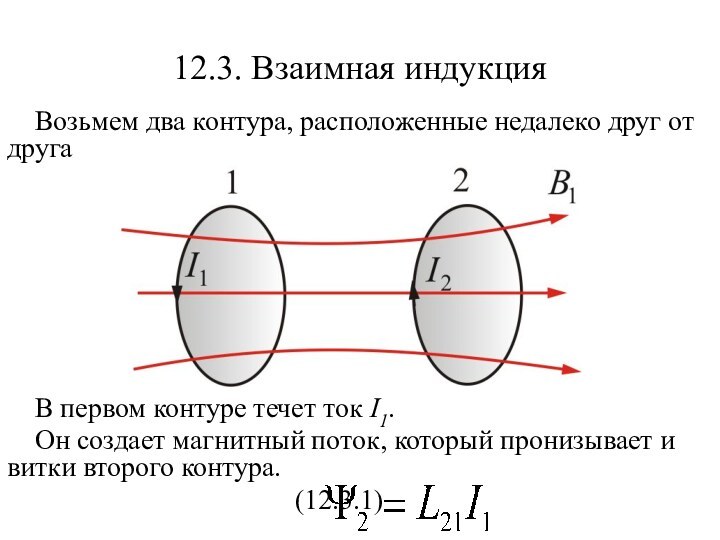
Возьмем два контура, расположенные недалеко друг

12.3. Взаимная индукцияВозьмем два контура, расположенные недалеко друг от другаВ первом

от друга

В первом контуре течет ток I1.
Он создает

магнитный поток, который пронизывает и витки второго контура.
(12.3.1)

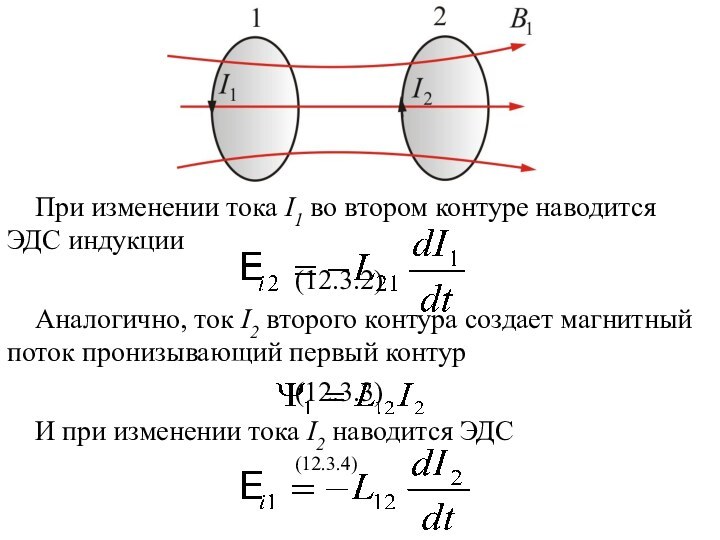
Слайд 18 При изменении тока I1 во втором контуре наводится

При изменении тока I1 во втором контуре наводится ЭДС индукции (12.3.2)Аналогично, ток

ЭДС индукции
(12.3.2)
Аналогично, ток I2 второго контура создает магнитный поток

пронизывающий первый контур
(12.3.3)
И при изменении тока I2 наводится ЭДС
(12.3.4)

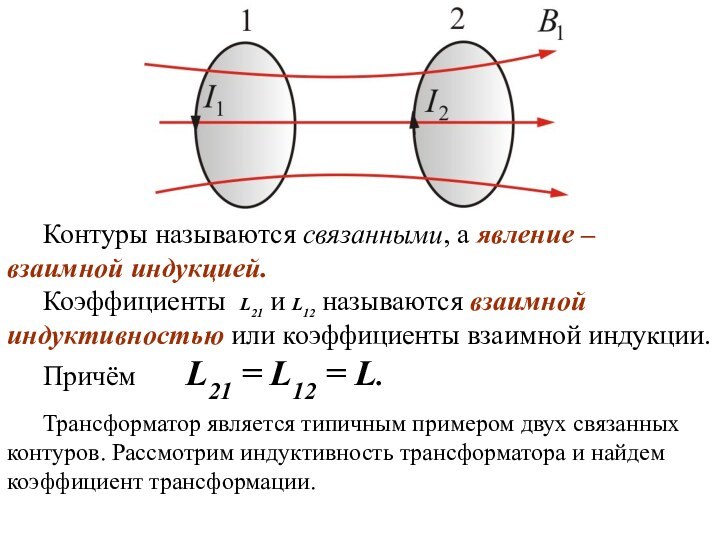
Слайд 19 Контуры называются связанными, а явление – взаимной индукцией.

Контуры называются связанными, а явление – взаимной индукцией. Коэффициенты L21 и

Коэффициенты L21 и L12 называются взаимной индуктивностью или коэффициенты

взаимной индукции.
Причём L21 = L12 = L.

Трансформатор является типичным примером двух связанных контуров. Рассмотрим индуктивность трансформатора и найдем коэффициент трансформации.

Слайд 20
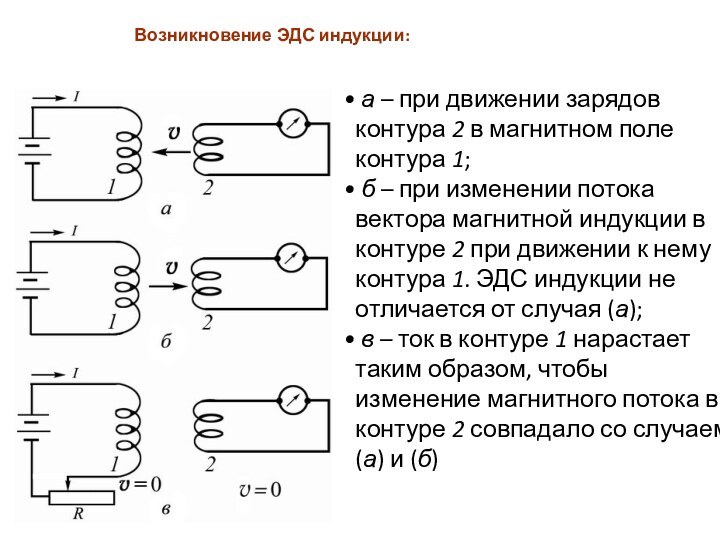
а – при движении зарядов контура 2

а – при движении зарядов контура 2 в магнитном поле

в магнитном поле контура 1;
б – при изменении

потока вектора магнитной индукции в контуре 2 при движении к нему контура 1. ЭДС индукции не отличается от случая (а);
в – ток в контуре 1 нарастает таким образом, чтобы изменение магнитного потока в контуре 2 совпадало со случаем (а) и (б)

Возникновение ЭДС индукции:

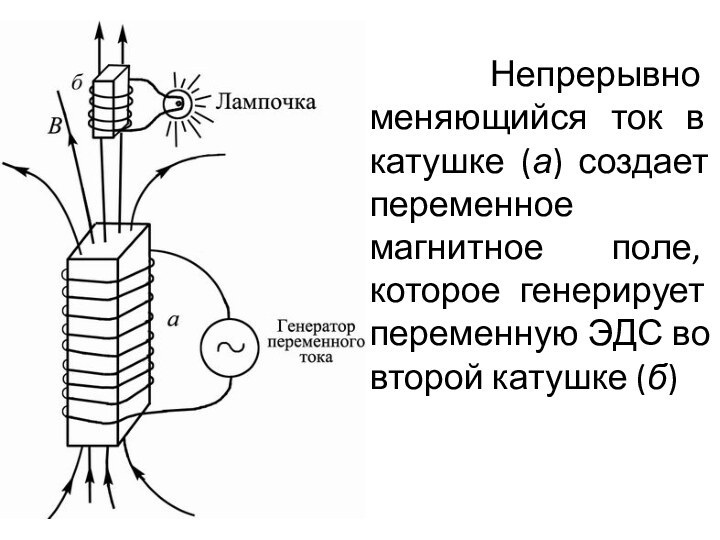
Слайд 21 Непрерывно меняющийся ток в катушке (а)

создает переменное магнитное поле, которое генерирует переменную ЭДС во

второй катушке (б)

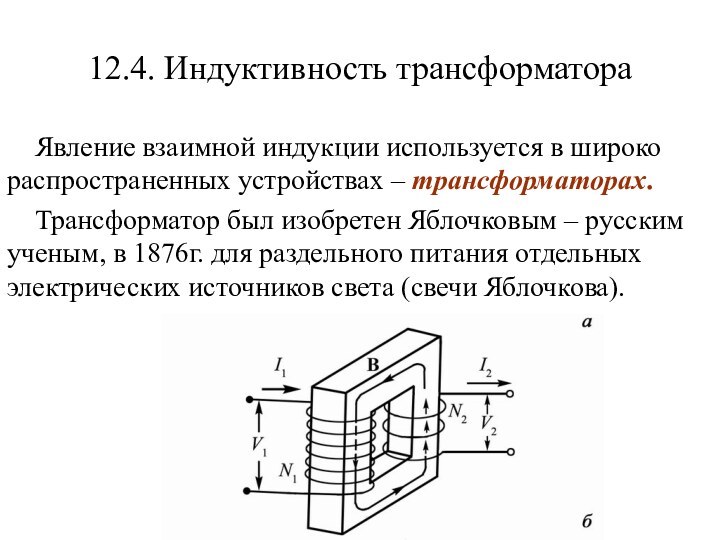
Слайд 22 12.4. Индуктивность трансформатора
Явление взаимной индукции используется в широко

12.4. Индуктивность трансформатораЯвление взаимной индукции используется в широко распространенных устройствах –

распространенных устройствах – трансформаторах.
Трансформатор был изобретен Яблочковым – русским

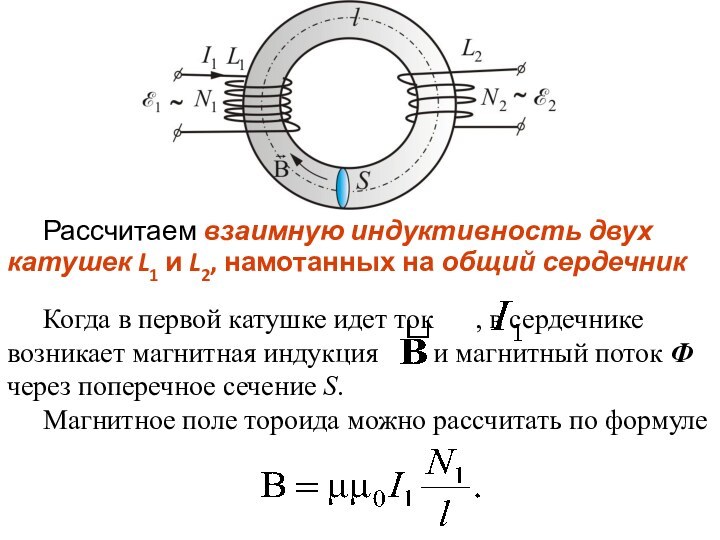
ученым, в 1876г. для раздельного питания отдельных электрических источников света (свечи Яблочкова).

Слайд 23 Рассчитаем взаимную индуктивность двух катушек L1 и L2,

Рассчитаем взаимную индуктивность двух катушек L1 и L2, намотанных на общий

намотанных на общий сердечник
Когда в первой катушке идет

ток , в сердечнике возникает магнитная индукция и магнитный поток Ф через поперечное сечение S.
Магнитное поле тороида можно рассчитать по формуле

Слайд 24 Через вторую обмотку проходит полный магнитный поток Ψ2

Через вторую обмотку проходит полный магнитный поток Ψ2 сцепленный со второй

сцепленный со второй обмоткой
(12.4.2)

К первичной обмотке подключена переменная ЭДС

E1.
По закону Ома ток в этой цепи будет определятся алгебраической суммой внешней ЭДС и ЭДС индукции.
(12.4.3)

где R1 – сопротивление обмотки.
R1 – делают малым (медные провода) и

Слайд 25 Тогда переменная ЭДС в первичной обмотке:

Тогда переменная ЭДС в первичной обмотке: (12.4.4)Во вторичной обмотке, по

(12.4.4)

Во вторичной обмотке, по аналогии

отсюда

(12.4.5)

Если пренебречь потерями, предположить, что R » 0, то
E1I1 » E2I2 (12.4.6)

Коэффициент трансформации

Слайд 26 12.5. Энергия магнитного поля
Рассмотрим случай, о котором мы

12.5. Энергия магнитного поляРассмотрим случай, о котором мы уже говорили: Сначала замкнем

уже говорили:

Сначала замкнем соленоид L на источник ЭДС E0.

В нем будет протекать ток I0.
Затем в момент времени t0 переключим ключ в положение 2 – замкнем соленоид на сопротивление R.
В цепи будет течь убывающий ток I.
Будет совершена работа: dA = EiIdt (12.5.1)

Слайд 27

(12.5.2)

Эта работа пойдет на

(12.5.2)Эта работа пойдет на нагревание проводников. Но откуда взялась

нагревание проводников.
Но откуда взялась эта энергия? Поскольку других

изменений кроме исчезновения магнитного поля в окружном пространстве не произошло, остается заключить: энергия была локализована в магнитном поле.
Значит, проводник, с индуктивностью L, по которой течет ток I, обладает энергией

(12.5.3)