- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Транспортная задача
Содержание
- 2. Описание транспортной задачи
- 3. Решить транспортную задачу – это найти оптимальный
- 4. Общая стоимость перевозок F, выраженная в тонно-километраххіjсіj - количество тонно-километровая характеристика перевозки.
- 6. Нахождение оптимального плана перевозок (х11, х12,….). Сводится
- 7. Примечание Если сij означает расстояния между базами
- 8. Если суммарный объем груза, содержащийся на базах,
- 11. 1. Формирование опорного решения
- 12. Формирование опорного решения методом северо-западного углаВначале заполняется
- 18. Стоимость перевозок по опорному (первоначальному) плану составит:
- 19. Решение транспортной задачи методом потенциалов
- 20. Пересчитывать опорный план можно с помощью потенциалов.
- 22. Значение одного из данных неизвестных можно выбирать
- 23. Значение одного из данных неизвестных можно выбирать
- 24. .Посчитаем алгебраические суммы свободных клетокs14 = c14
- 25. Тариф свободной клетки обозначают как cij и
- 26. Новая стоимость перевозок находится по формуле: Т.е стоимость перевозок уменьшится на число:
- 27. 3. Циклы пересчета в таблице перевозок
- 28. Для уменьшения стоимости перевозок используются циклы пересчета.
- 29. в каждый цикл может входить только одна
- 30. Если для свободной клетки исходной таблицы, заполненной
- 31. Перераспределение груза происходит по следующим правилам:а) снабдим
- 32. Циклы пересчета №1Выбрали свободную клетку, построил цикл.
- 33. Циклы пересчета №1Расставили знаки
- 34. Циклы пересчета №1в клетках, отмеченных знаком () выберем наименьшее из чисел
- 35. Циклы пересчета №1Из клеток, отмеченных знаком (),
- 36. F = 70·170 + 50·110 +
- 37. Следует сравнить стоимость перевозок в каждом цикле
- 38. Примечание. Если минимальное значение среди базисных переменных
- 39. 4. Критерий оптимальности решения транспортной задачи
- 40. Изменение стоимости перевозок в каждом цикле связано
- 41. Факт увеличения или уменьшения стоимости перевозок определяется
- 42. Критерий оптимальности решенияОчередное решение определяет оптимальный план
- 44. Циклы пересчета строятся только для тех свободных клеток, для которых алгебраические суммы тарифов отрицательны.
- 45. Принимается наибольшее уменьшение стоимости перевозок.Строим таблицу, соответствующую самому выгодному циклу:
- 47. К новой таблице применяют еще раз метод
- 48. Fопт. = 70 ·140 + 50 ·
- 49. Скачать презентацию
- 50. Похожие презентации
Описание транспортной задачи




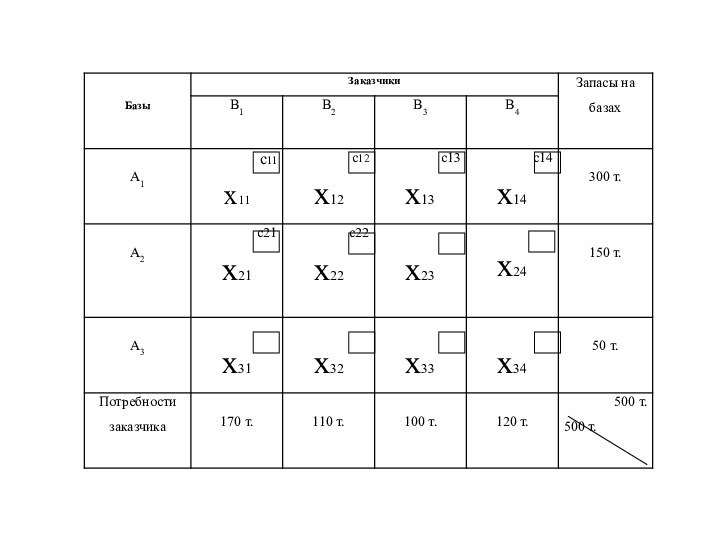



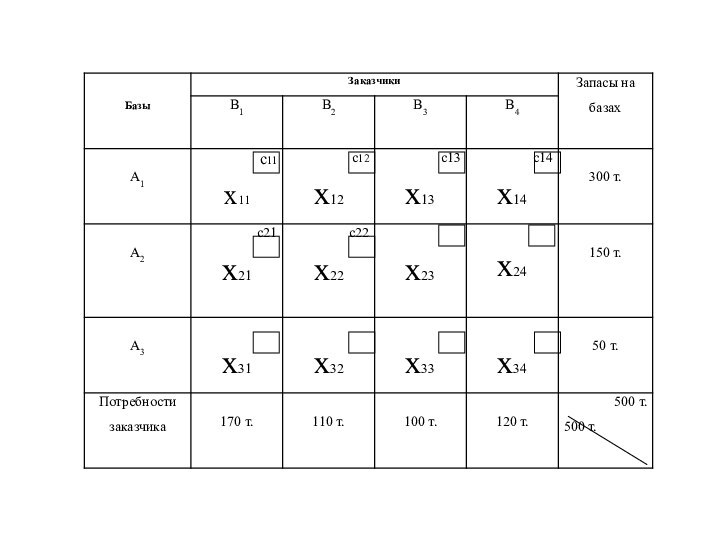


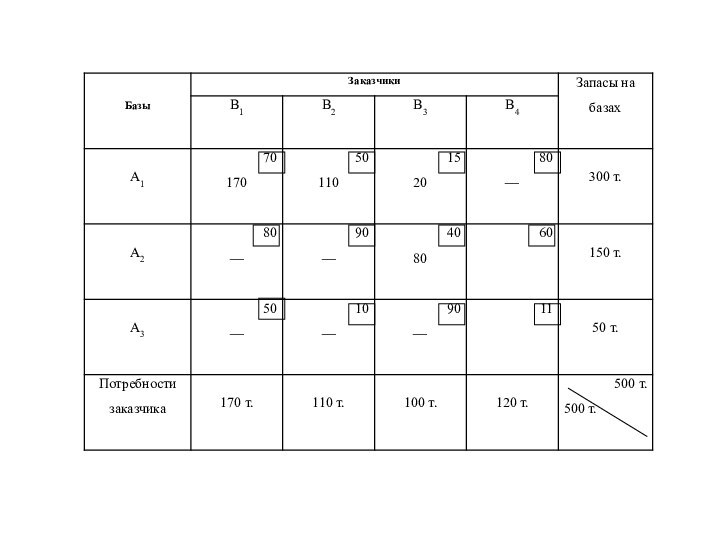


























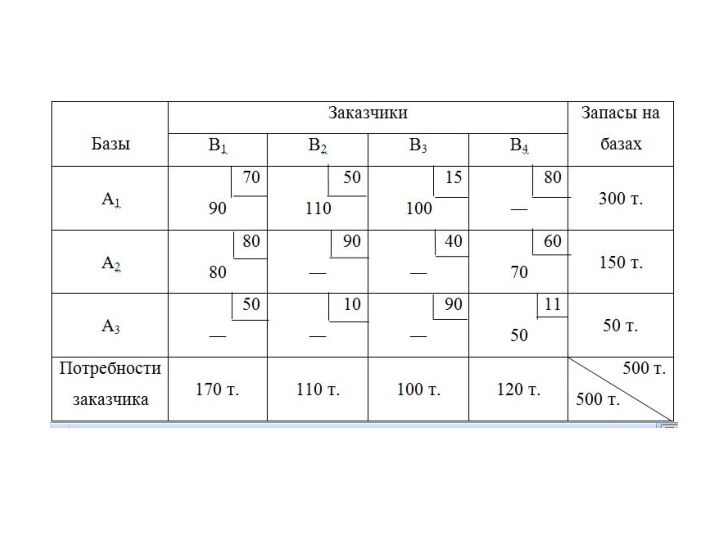


Слайд 3 Решить транспортную задачу – это найти оптимальный план
перевозок (х11, х12,…, х34), который минимизирует его стоимость перевозок.
Слайд 4
Общая стоимость перевозок F, выраженная в тонно-километрах
хіjсіj -
количество тонно-километровая характеристика перевозки.
Слайд 6 Нахождение оптимального плана перевозок (х11, х12,….). Сводится к
решению системы линейных уравнений, относительно определяемых переменных хіj
х11
+ х12 + х13 + х14 = 300,х21 + х22 + х23 + х24 = 150,
х31 + х32 + х33 + х34 = 50,
х11 + х21 + х31 = 170,
х12 + х22 + х32 = 110,
х13 + х23 + х33 = 100,
х14 + х24+ х34 = 120.
Слайд 7
Примечание
Если сij означает расстояния между базами и
заказчиками, то F (общая стоимость) выражается в в тонно-километрах.
Если
сij означает стоимость перевозки одной тонны груза между базами и заказчиками, то F (общая стоимость) выражается в рублях. Слайд 8 Если суммарный объем груза, содержащийся на базах, равен
суммарной потребности заказчиков, то транспортная задача называется закрытой или
сбалансированной.(то есть, при вывозе всего груза, имеющегося на базах, потребности всех заказчиков будут полностью удовлетворены)
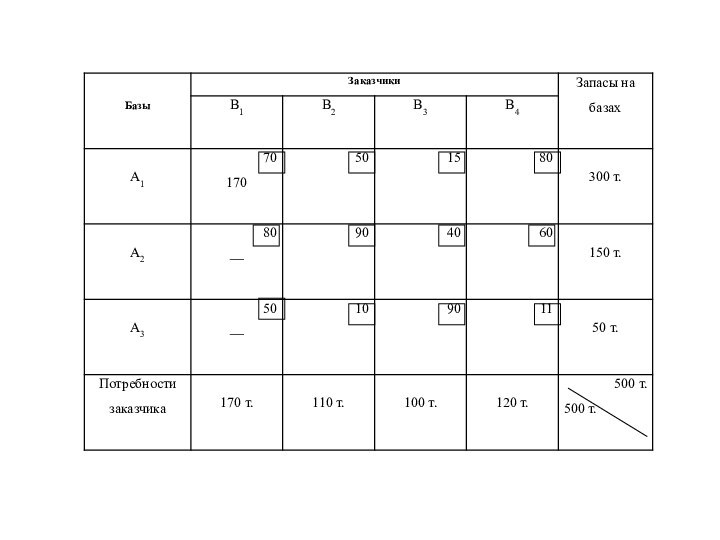
Слайд 12
Формирование опорного решения методом северо-западного угла
Вначале заполняется левая
верхняя клетка (северо-западный угол) исходной таблицы или её оставшейся
части.После заполнения северо-западного угла с учетом предельных возможностей базы, из таблицы исключается или очередной столбец слева, или очередная строка сверху.
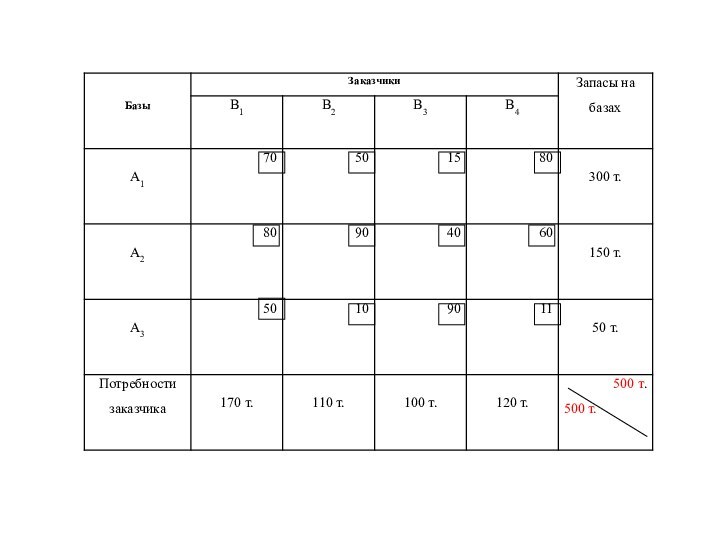
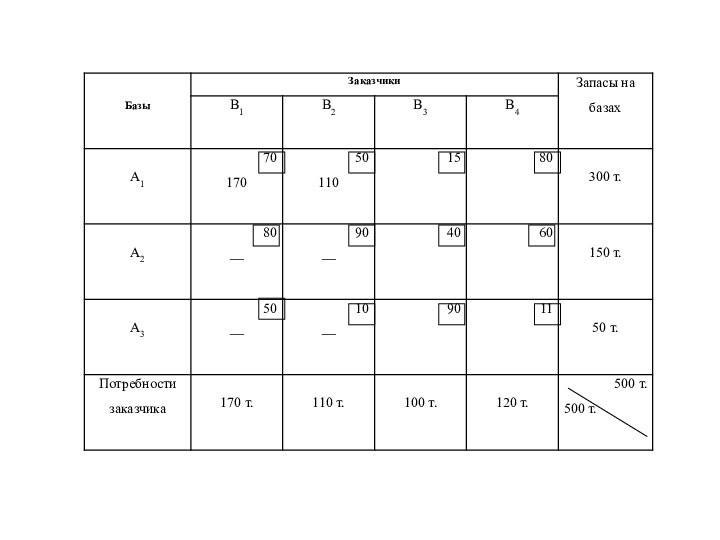
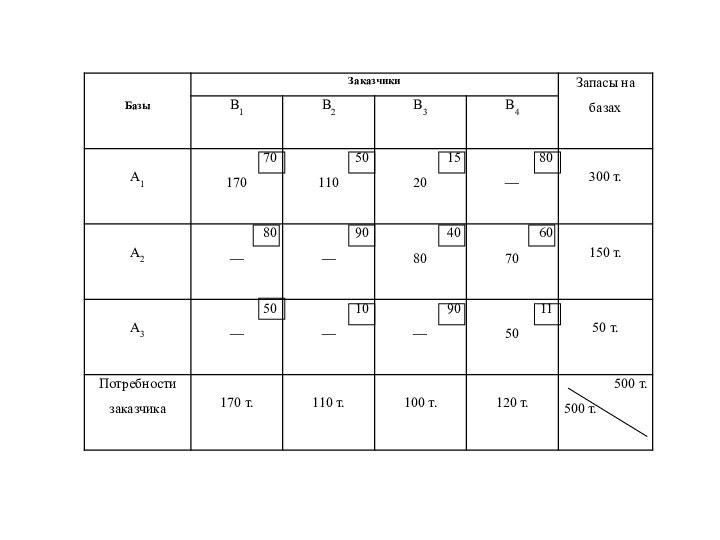
Слайд 18 Стоимость перевозок по опорному (первоначальному) плану составит: Fнач =
70·170 + 50·110 + 15·20 + 40·80 + 60·70
+ 11·50 = 25650 (т.км.)Слайд 20 Пересчитывать опорный план можно с помощью потенциалов. Тариф
сij базисных переменных представляется в виде суммы сij
= αi - потенциалы баз, βj – потенциалы заказчиков.Слайд 22 Значение одного из данных неизвестных можно выбирать произвольно.
Например, можно принять, что α1 = 0.
Тогда решение
системы примет вид:Слайд 23 Значение одного из данных неизвестных можно выбирать произвольно.
Например, можно принять, что α1 = 0.
Тогда решение
системы примет вид:α1 = 0, β1 = 70,
α2 = 25, β2 = 50,
α3 = – 24, β3 = 15,
β4 = 35
Слайд 24
.
Посчитаем алгебраические суммы свободных клеток
s14 = c14 –
c'14= 80 – (0 + 35) = 45
s21 =
c21 – c'21 = с21 – (α2 + β1) = 80 – (25 + 70) = 15,s22 = c22 – c'22 = с22 – (α2 + β2) = 90 – (25 + 50) = 15,
s31 = c31 – c'31 = с31 – (α3 + β1) = 50 – (–24 + 70) = 4,
s32 = c32 – c'32 = с32 – (α3 + β2) = 10 – (–24 + 50) = 16,
s33 = c33 – c'33 = с33 – (α3 + β3) = 90 – (–24 + 15) = 99.
Слайд 25 Тариф свободной клетки обозначают как cij и называют
косвенным тарифом. Сравнение тарифов свободной клетки определяется разностью истинного
и косвенного тарифов. sij = cij – c‘ij
Слайд 26
Новая стоимость перевозок находится по формуле:
Т.е
стоимость перевозок уменьшится на число:
Слайд 28 Для уменьшения стоимости перевозок используются циклы пересчета. Циклом пересчета
в таблице перевозок называется последовательность переменных хіj, удовлетворяющих следующим
условиям:Слайд 29 в каждый цикл может входить только одна свободная
переменная (клетка с прочерком). Все остальные переменные должны быть
базисными (заполненные клетки);каждые две последовательные переменные, входящие в цикл, могут находиться только на одной строке или только в одном столбце;
каждая строка или столбец данного цикла может содержать только две переменные;
каждый цикл замкнут (т.е при последовательном обходе выбранных переменных цикл начинается и заканчивается одной и той же клеткой).
Слайд 30 Если для свободной клетки исходной таблицы, заполненной методом
северо-западного угла, можно построить цикл пересчета, то такой цикл
является единственным. Число вершин в этом цикле чётно.Если же для какой-либо свободной клетки исходной таблицы цикл пересчета построить нельзя, то для реализации этой возможности некоторые из свободных переменных обращаются в базисные переменные с нулевыми значениями (в пустых клетках записываются нули). Решение, содержащее нулевые значения базисных переменных, называется вырожденным.
Слайд 31
Перераспределение груза происходит по следующим правилам:
а) снабдим свободную
клетку знаком (+) и с каждым переходом к следующей
клетке цикла будем изменять знак на противоположный;б) в клетках, отмеченных знаком () выберем наименьшее из чисел. Это то количество груза, которое будет последовательно перевозиться из одной клетки в другую.
Из клеток, отмеченных знаком (), зафиксированное количество груза вывозится; в клетках со знаком (+) – прибывает.
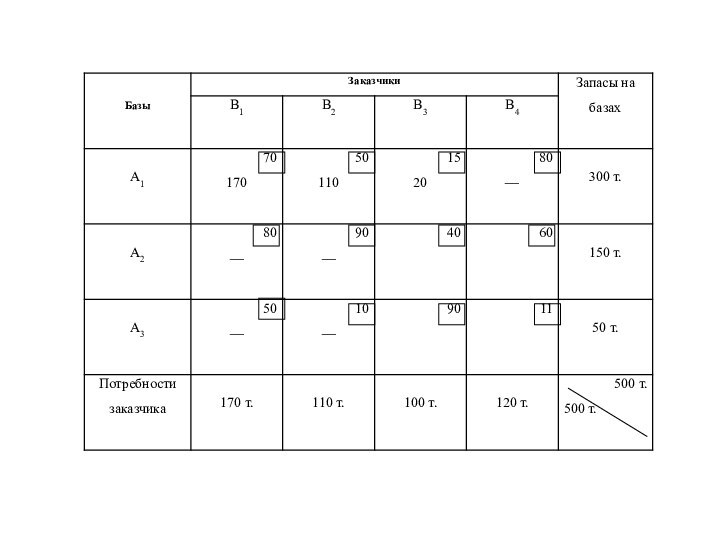
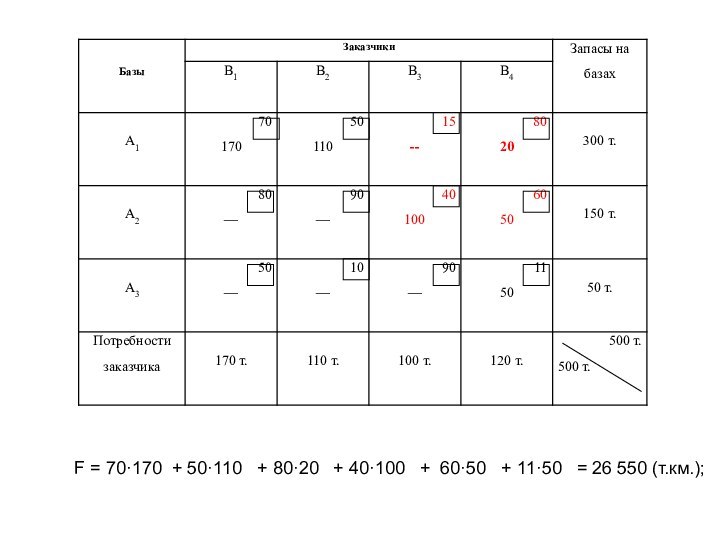
Слайд 35
Циклы пересчета №1
Из клеток, отмеченных знаком (), зафиксированное
количество груза вычтем; в клетках со знаком (+) –
прибавим.(результат запишем ниже)Слайд 37 Следует сравнить стоимость перевозок в каждом цикле со
стоимостью перевозок по опорному (первоначальному) плану
Fнач = 25650 (т.км.)
и
выбрать наименьший из всех результатовСлайд 38 Примечание. Если минимальное значение среди базисных переменных содержится
в цикле пересчета в нескольких отрицательных вершинах цикла, то
свободной (с прочерком) оставляют только одну из них, а в других клетках с таким же минимальным значением записываются нули. Эти нули являются новыми значениями базисных переменных. Образуется вырожденное решение.Слайд 40 Изменение стоимости перевозок в каждом цикле связано с
числом m (фиксированное число цикла)
(Если вершина снабжена знаком
(+), то это количество груза на m увеличивается; () на m уменьшается.) Стоимость перевозок можно пересчитать по формуле:
m · с14 – m · с13 + m · с23 – m · с24 = (с14 – с13 + с23 – с24) · m
= (80 – 15 + 40 – 60) · 20 = 45 · 20 = 900
900= 26 550 – 25 650 (т.км.).
Слайд 41 Факт увеличения или уменьшения стоимости перевозок определяется не
количеством перевозимого груза, а знаком алгебраической суммы тарифов по
данному циклу
Слайд 42
Критерий оптимальности решения
Очередное решение определяет оптимальный план перевозок,
если алгебраические суммы тарифов для всех возможных циклов пересчета
больше или равны нулю или в наилучшем цикле пересчета при отрицательном значении алгебраической суммы тарифов количество перевозимого груза равно нулюСлайд 44 Циклы пересчета строятся только для тех свободных клеток,
для которых алгебраические суммы тарифов отрицательны.
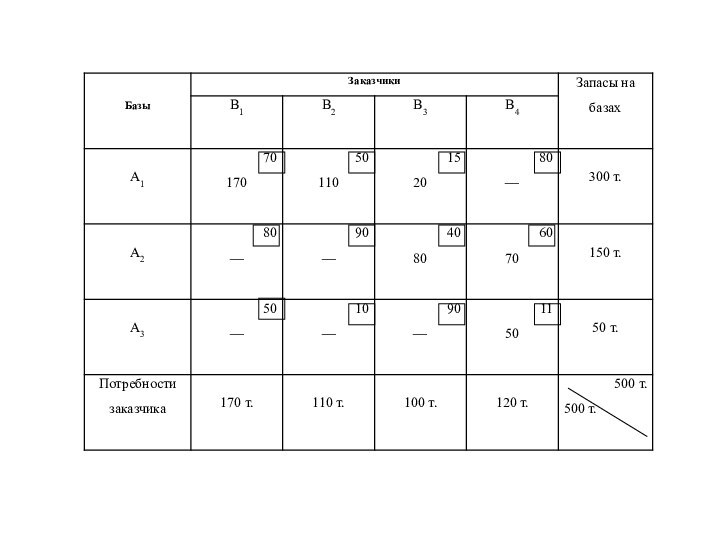
Слайд 45
Принимается наибольшее уменьшение стоимости перевозок.
Строим таблицу, соответствующую самому
выгодному циклу:
Слайд 47 К новой таблице применяют еще раз метод потенциалов
для минимизации стоимости перевозок до тех пор, пока алгебраические
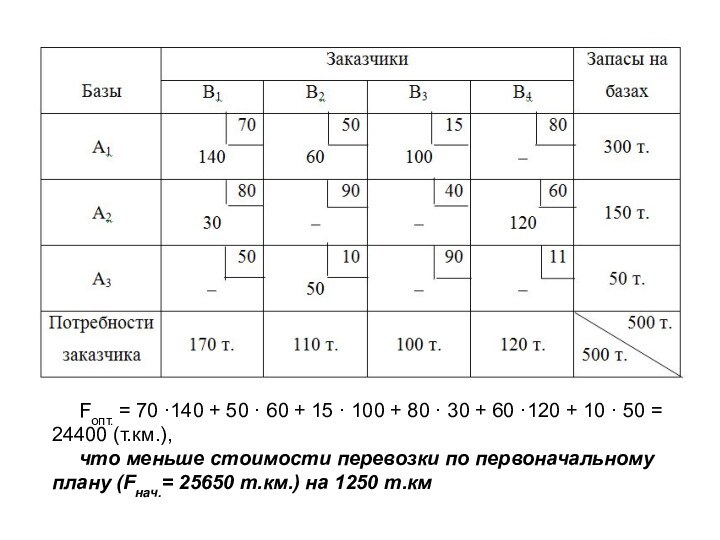
суммы тарифов для всех свободных клеток таблицы не окажутся положительными.Слайд 48 Fопт. = 70 ·140 + 50 · 60
+ 15 · 100 + 80 · 30 +
60 ·120 + 10 · 50 = 24400 (т.км.),что меньше стоимости перевозки по первоначальному плану (Fнач.= 25650 т.км.) на 1250 т.км