Слайд 2
УСЛОВИЯ МНОГОЛЕТНЕГО РЕГУЛИРОВАНИЯ :
Qг,Р% (Wг,Р%) - годовой расход
(объем) расчетной обеспеченности
Qгар (Wгар) – гарантированный расход(объем)
Qг (Wг) –
среднегодовой расход(объем)
кг,Р% – модульный коэффициент расчетной обеспеченности
α – коэффициент регулирования
Слайд 3
Vполезн.мн.=Wдеф.за малов. n-летие, р%
V полезн.мн. =V мн.сост. +Vсезон.сост.
Слайд 5
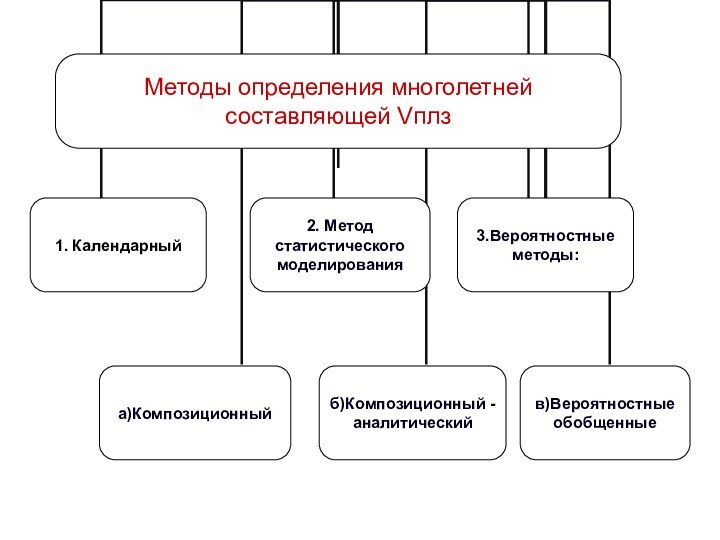
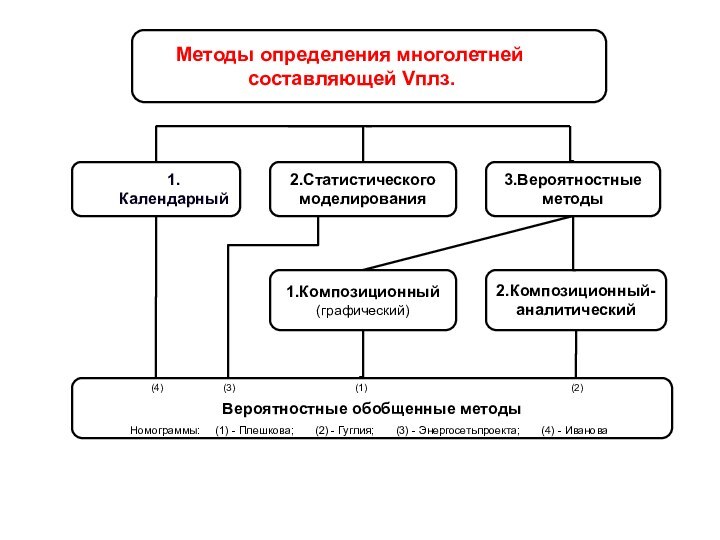
Методы определения многолетней
составляющей Vплз.
2.Статистического моделирования
3.Вероятностные методы
1. Календарный
1.Композиционный (графический)
2.Композиционный-аналитический
Вероятностные обобщенные методы
(2)
(1)
(3)
(4)
Номограммы: (1) - Плешкова; (2) - Гуглия; (3) - Энергосетьпроекта; (4) - Иванова
Слайд 6
Расчеты обычно ведутся в относительных величинах:
Qг
через
Qгар через
Vмн.с. через
Назначается расчетная обеспеченность
Р%
Требуется определить вероятность бесперебойных лет:
Рα=(1-S)*100%,
где S – вероятность наступления перебоев
Композиционный метод
Слайд 7
В вероятностном композиционном методе увязываются следующие характеристики:
Слайд 8
Графическое решение задачи
и условия возникновения
перебоя /
неперебоя в отдельно взятом году
1.Перебой БЕЗУСЛОВНО наступит, если
в отдаче
Вероятность наступления безусловно
перебойных лет равна
Слайд 9
2.Перебоя НИКОГДА не наступит, если
Вероятность неперебоя равна
Слайд 10
3. УСЛОВНО перебойные годы
Вероятность этих лет равна:
Слайд 11
Условия возникновения
перебоя / неперебоя в отдельно взятом
году
1. Перебой безусловно наступит, если в отдаче
Вероятность наступления безусловно перебойных лет равна
2. Перебоя никогда не наступит, если
Вероятность безусловно безперебойных лет
равна
3. Условно перебойные годы
Вероятность этих лет равна:
Слайд 12
Определение вероятности перебоя в двухлетке
Слайд 13
Условия возникновения
перебоя / неперебоя в двухлетке
1. Перебой
обязательно наступит, если
2. Перебой никогда не наступит, если
3.
Условно перебойная группа
Слайд 14
Условия возникновения
перебоя / неперебоя в двухлетке
1. Перебой
обязательно наступит, если
2. Перебой никогда не наступит, если
3.
Условно перебойная группа
Слайд 15
Определение вероятности перебоя в трехлетке
Условия возникновения
перебоя /
неперебоя в трехлетке
1. Перебой обязательно наступит, если
2.
Перебой никогда не наступит, если
3. Условно перебойная группа
Слайд 16
Общая безусловная суммарная вероятность наступления перебоя в маловодной
n-летки равна
S1 – безусловная вероятность наступления перебоя в отдельно
взятом году;
- условная вероятность перебоя в двухлетке,
трехлетке и т.д.;
U1, U2, …,Un - вероятность наступления условий 1,2,…,n
Слайд 17
В вероятностном композиционном методе увязываются следующие характеристики:
Слайд 18
НОМОГРАММА ПЛЕШКОВА
F(Cv;α;β;P%)=0
Слайд 19
Условия построения
номограмм Плешкова:
Функция распределения Пирсона III
типа.
Cv=0,1÷1,2
Сs=2 Cv
r(1)=0
α=0,1÷0,9
β=0÷4,3
P%=70%; 80%; 90%; 95%; 97%; 98%;
99%
Слайд 20
КОМПОЗИЦИОННЫЙ АНАЛИТИЧЕСКИЙ МЕТОД
КРИЦКОГО-МЕНКЕЛЯ
для рек России r(1)>0, в
среднем r(1)=0,3
К(r) – поправочный коэффициент, зависящий от степени внутрирядной
связанности стока
Слайд 22
УСЛОВИЯ, ПРИ КОТРОРЫХ СОСТАВЛЕННЫ НОМОГРАММЫ ГУГЛИЯ:
Функция распределения Пирсона
III типа
Cv=0,1÷1,2
Сs=2 Cv
r(1)=0,3(для большинства рек России)
α=0,2÷0,95
β=0÷4,5
P%=75%; 90%; 95%; 97%;
99%
Слайд 23
Пример роли внутрирядной связанности в оценке величины полезной
емкости водохранилища
Слайд 24
Оценка βмн.с. по номограммам Плешкова и Гуглия при
различных значениях r(1)
Слайд 25
МЕТОД СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ
МОНТЕ-КАРЛО
НОМОГРАММЫ ЭНЕРГОСЕТЬПРОЕКТА
F(CV,CS,r(1),α,β,P%)
Условия при которых
составлены номограммы:
Функция распределения Пирсона III типа
Трехмерное γ-распределение (Крицкого-Менкеля)
Cv=0,1÷1,5
Сs=2 Cv
(Пирсона III типа = Крицкого-Менкеля)
Сs=1,5 Cv (Крицкого-Менкеля)
Сs=4,0 Cv (Крицкого-Менкеля)
r(1)=0,0÷0,6
α=0,1÷1,0
βмн=0,0÷3,0
P%=75%; 80%; 85%; 90%; 95%; 97%; 99%
Слайд 27
НОМОГРАММЫ ИВАНОВА Г.П.
Нормированные значения коэффициентов регулирования
и относительной полезной ёмкости водохранилища:
Слайд 29
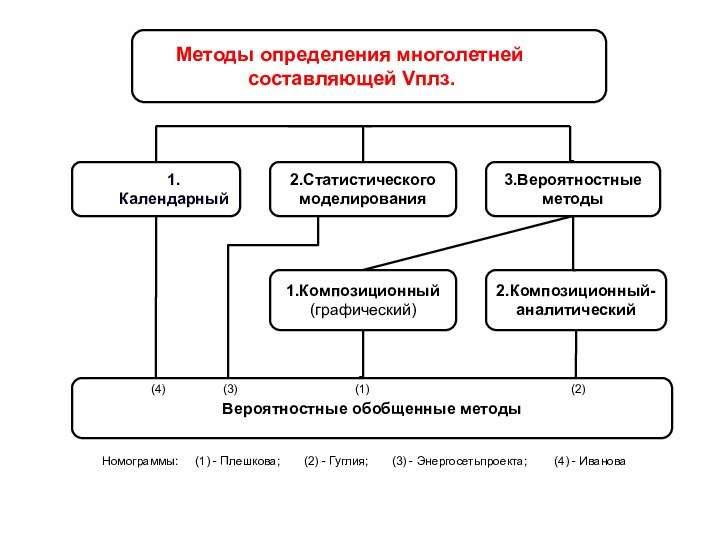
Методы определения многолетней
составляющей Vплз.
2.Статистического моделирования
3.Вероятностные методы
1. Календарный
1.Композиционный (графический)
2.Композиционный-аналитический
Вероятностные обобщенные методы
(2)
(1)
(3)
(4)
Номограммы: (1) - Плешкова; (2) - Гуглия; (3) - Энергосетьпроекта; (4) - Иванова